問題:相似な図形と相似比
次の問いに答えよ。
\({\small (1)}~\)次の四角形 \({\rm ABCD}\) と四角形 \({\rm EFGH}\) が相似であり、相似比が \(2:3\) である。
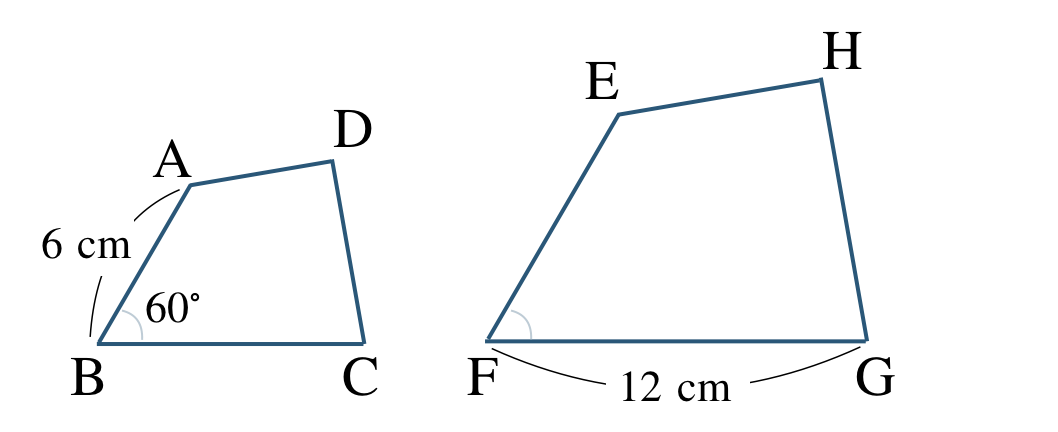
① 相似であることを記号で表せ。
② 辺 \({\rm EF}\) の長さを求めよ。
③ 辺 \({\rm BC}\) の長さを求めよ。
④ \(\angle {\rm F}\) の大きさを求めよ。
\({\small (2)}~\)次の三角形 \({\rm ABC}\) と三角形 \({\rm DEF}\) が相似である。
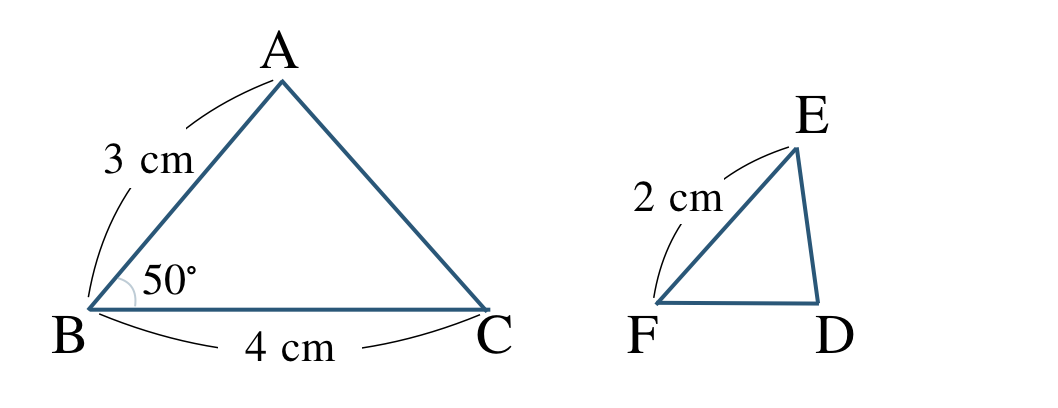
① 相似であることを記号で表せ。
② 相似比を求めよ。
③ 辺 \({\rm DE}\) の長さを求めよ。
④ \(\angle {\rm E}\) の大きさを求めよ。
\({\small (3)}~\)相似比が \(1:1\) の2つの三角形はどのような関係か答えよ。
解法のPoint
2つの図形の一方を拡大または縮小した図形が、もとの図形と合同であるとき、この2つの図形は「相似」であるという。
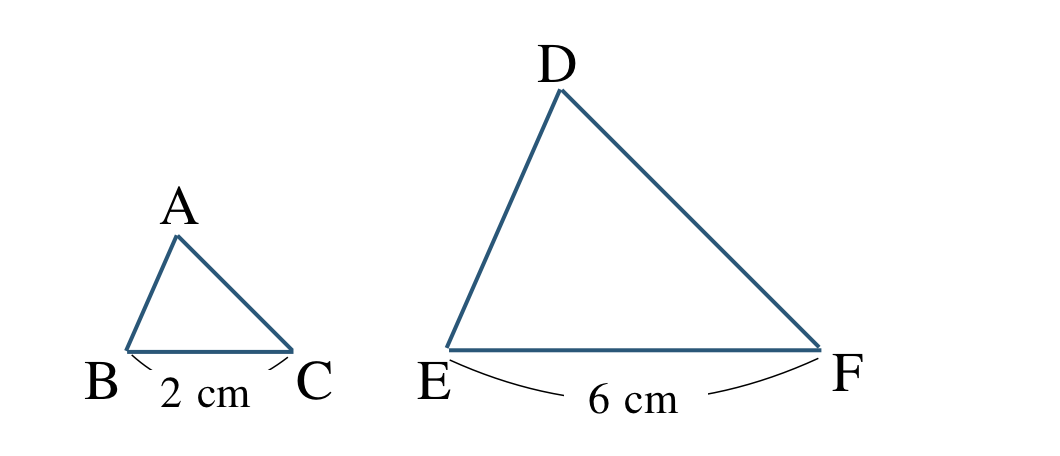
\(\triangle {\rm ABC}\) と \(\triangle {\rm DEF}\) が相似であるとき、
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm DEF}\)
相似な図形では、
\({\small (1)}~\)対応する線分の長さの比は、すべて等しい。
また、この比を「相似比」という。
\(~~~{\rm AB:DE=BC:EF=AC:DF}\)
上の図で相似比は \(1:3\) となる。
\({\small (2)}~\)対応する角の大きさは、それぞれ等しい。
\(~~~{\rm \angle A=\angle D~,~\angle B=\angle E~,~\angle C=\angle F}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:相似な図形と相似比
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の四角形 \({\rm ABCD}\) と四角形 \({\rm EFGH}\) が相似であり、相似比が \(2:3\) である。

① 相似であることを記号で表せ。
② 辺 \({\rm EF}\) の長さを求めよ。
③ 辺 \({\rm BC}\) の長さを求めよ。
④ \(\angle {\rm F}\) の大きさを求めよ。
① 四角形 \({\rm ABCD}\) と四角形 \({\rm EFGH}\) が相似であるので、
四角形 \({\rm ABCD}\) \(\,\,\unicode{x223D}\,\,\) 四角形 \({\rm EFGH}\)
となる
② 相似な図形では、対応する線分の長さの比が相似比 \(2:3\) と等しいので、
\(\begin{eqnarray}~~~{\rm AD:EF}&=&2:3\\[2pt]~~~6:{\rm EF}&=&2:3\\[2pt]~~~{\rm EF}\times2&=&6\times3\\[3pt]~~~\frac{\,2{\rm EF}\,}{\,2\,}&=&\frac{\,18\,}{\,2\,}\\[3pt]~~~{\rm EF}&=&9\end{eqnarray}\)
したがって、\({\rm EF}=9~{\rm cm}\) となる
③ 相似な図形では、対応する線分の長さの比が相似比 \(2:3\) と等しいので、
\(\begin{eqnarray}~~~{\rm BC:FG}&=&2:3\\[2pt]~~~{\rm BC}:12&=&2:3\\[2pt]~~~{\rm BC}\times3&=&12\times2\\[3pt]~~~\frac{\,3{\rm BC}\,}{\,3\,}&=&\frac{\,24\,}{\,3\,}\\[3pt]~~~{\rm BC}&=&8\end{eqnarray}\)
したがって、\({\rm BC}=8~{\rm cm}\) となる
④ 相似な図形では、対応する角の大きさは、それぞれ等しいので、
\(~~~\angle {\rm F}=\angle {\rm D}=60^\circ\)
したがって、\(\angle {\rm F}=60^\circ\) となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の三角形 \({\rm ABC}\) と三角形 \({\rm DEF}\) が相似である。

① 相似であることを記号で表せ。
② 相似比を求めよ。
③ 辺 \({\rm DE}\) の長さを求めよ。
④ \(\angle {\rm E}\) の大きさを求めよ。
① \(\triangle {\rm ABC}\) と \(\triangle {\rm DEF}\) の向きをそろえてかくと、
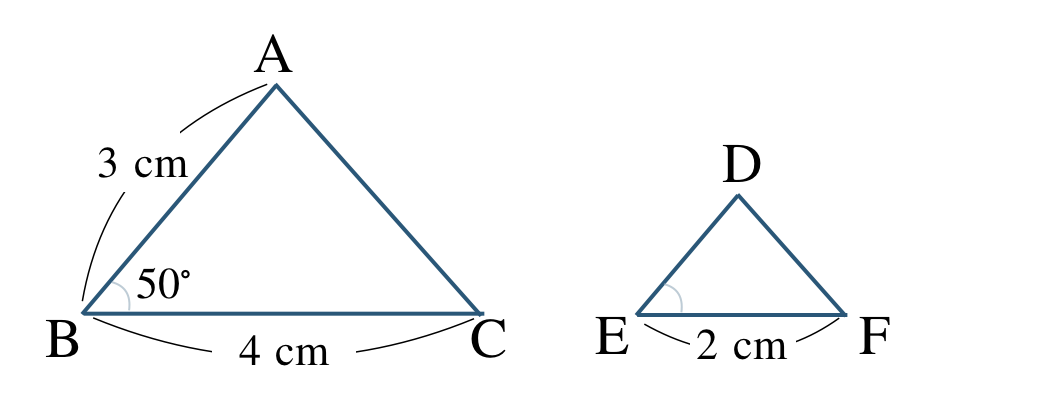
これより、\(triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm DEF}\) となる
② 相似な図形では、対応する線分の長さの比が相似比と等しいので、
\(\begin{eqnarray}~~~{\rm BC:EF}&=&4:2\\[3pt]~~~&=&\frac{\,4\,}{\,2\,}:\frac{\,2\,}{\,2\,}\\[3pt]~~~&=&2:1\end{eqnarray}\)
したがって、相似比 \(2:1\) となる
③ 相似な図形では、対応する線分の長さの比が相似比 \(2:1\) と等しいので、
\(\begin{eqnarray}~~~{\rm AB:DE}&=&2:1\\[2pt]~~~3:{\rm DE}&=&2:1\\[2pt]~~~{\rm DE}\times2&=&3\times1\\[3pt]~~~\frac{\,2{\rm DE}\,}{\,2\,}&=&\frac{\,3\,}{\,2\,}\\[3pt]~~~{\rm DE}&=&\frac{\,3\,}{\,2\,}\end{eqnarray}\)
したがって、\(\begin{split}{\rm DE}=\frac{\,3\,}{\,2\,}~{\rm cm}~~~(~1.5~{\rm cm}~)\end{split}\) となる
\({\large ④}~\)相似な図形では、対応する角の大きさは、それぞれ等しいので、
\(~~~\angle {\rm E}=\angle {\rm B}=50^\circ\)
したがって、\(\angle {\rm E}=50^\circ\) となる
問題解説(3)
次の問いに答えよ。
\({\small (3)}~\)相似比が \(1:1\) の2つの三角形はどのような関係か答えよ。
相似比が \(1:1\) のとき、
対応する線分の長さが、それぞれ等しくなるので、
この2つの三角形は合同
である



