このページは「中学数学3 相似な図形」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学3 相似な図形
相似な図形と相似比
次の問いに答えよ。
\({\small (1)}~\)次の四角形 \({\rm ABCD}\) と四角形 \({\rm EFGH}\) が相似であり、相似比が \(2:3\) である。
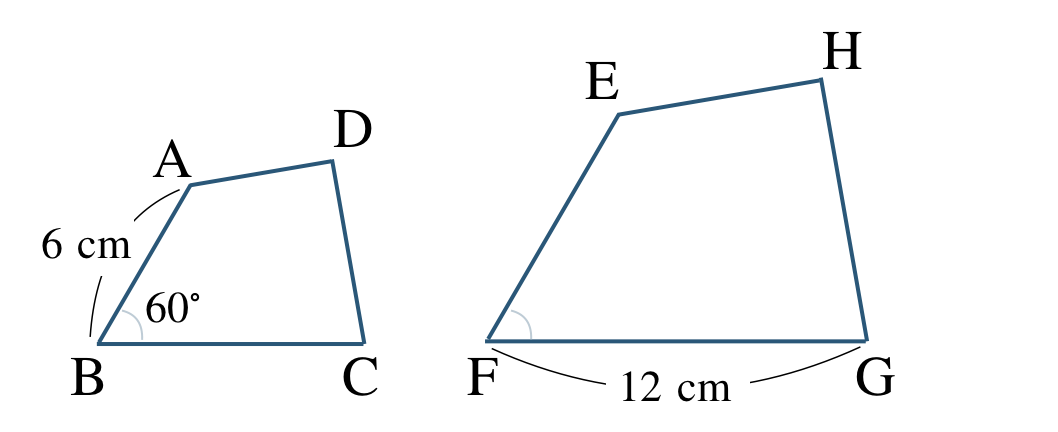
① 相似であることを記号で表せ。
② 辺 \({\rm EF}\) の長さを求めよ。
③ 辺 \({\rm BC}\) の長さを求めよ。
④ \(\angle {\rm F}\) の大きさを求めよ。
\({\small (2)}~\)次の三角形 \({\rm ABC}\) と三角形 \({\rm DEF}\) が相似である。
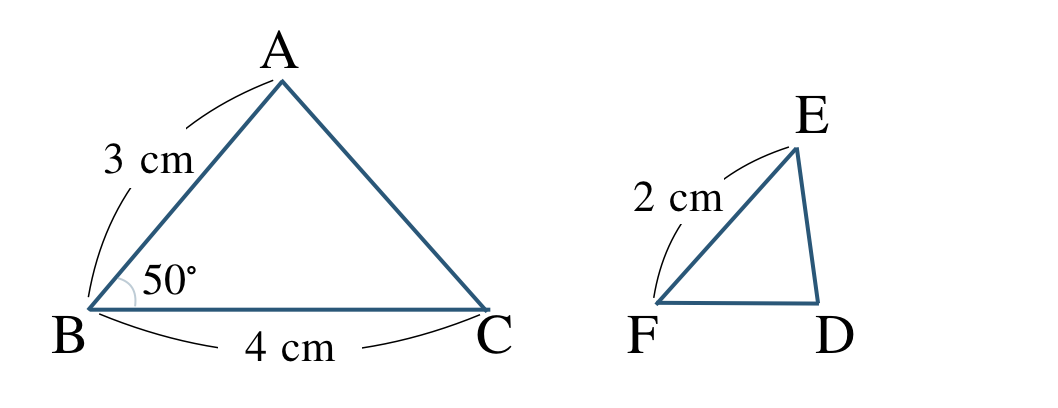
① 相似であることを記号で表せ。
② 相似比を求めよ。
③ 辺 \({\rm DE}\) の長さを求めよ。
④ \(\angle {\rm E}\) の大きさを求めよ。
\({\small (3)}~\)相似比が \(1:1\) の2つの三角形はどのような関係か答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 四角形 \({\rm ABCD}\) \(\,\,\unicode{x223D}\,\,\) 四角形 \({\rm EFGH}\)
② \({\rm EF}=9~{\rm cm}\)
③ \({\rm BC}=8~{\rm cm}\)
④ \(\angle {\rm F}=60^\circ\)
\({\small (2)}~\)
① \(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm DEF}\)
② 相似比 \(2:1\)
③ \(\begin{split}{\rm DE}={ \frac{\,3\,}{\,2\,}}~{\rm cm}~~~(~1.5~{\rm cm}~)\end{split}\)
④ \(\angle {\rm E}=50^\circ\)
\({\small (3)}~\)この2つの三角形は合同

相似の位置
次の問いに答えよ。
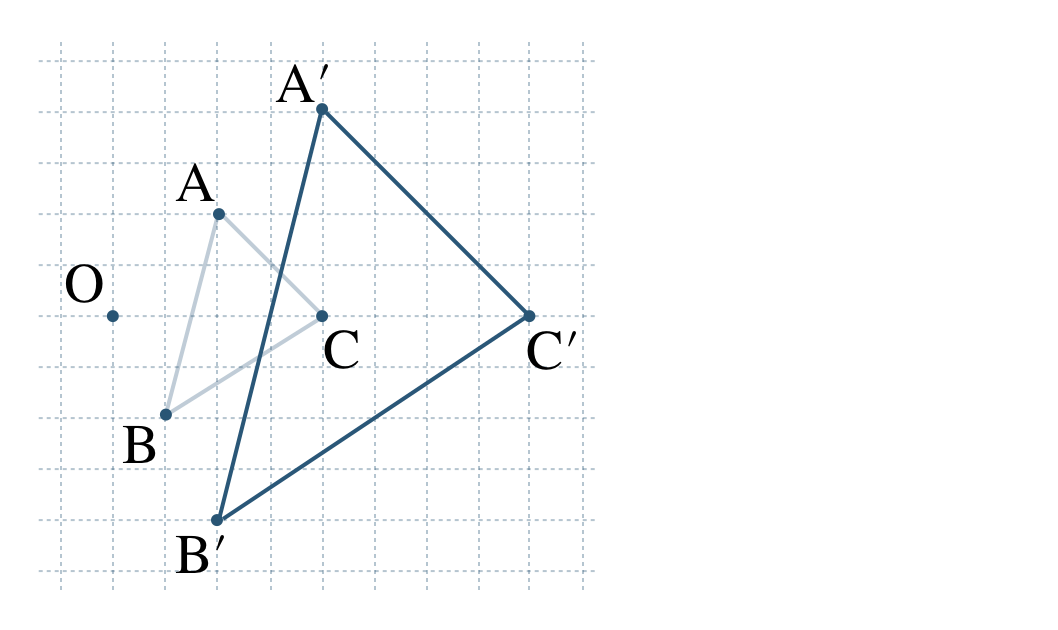
\({\small (1)}~\)次の図に、点 \({\rm O}\) を相似の中心として、\(\triangle {\rm ABC}\) を \(2\) 倍に拡大した \(\triangle {\rm A’B’C’}\) をかけ。
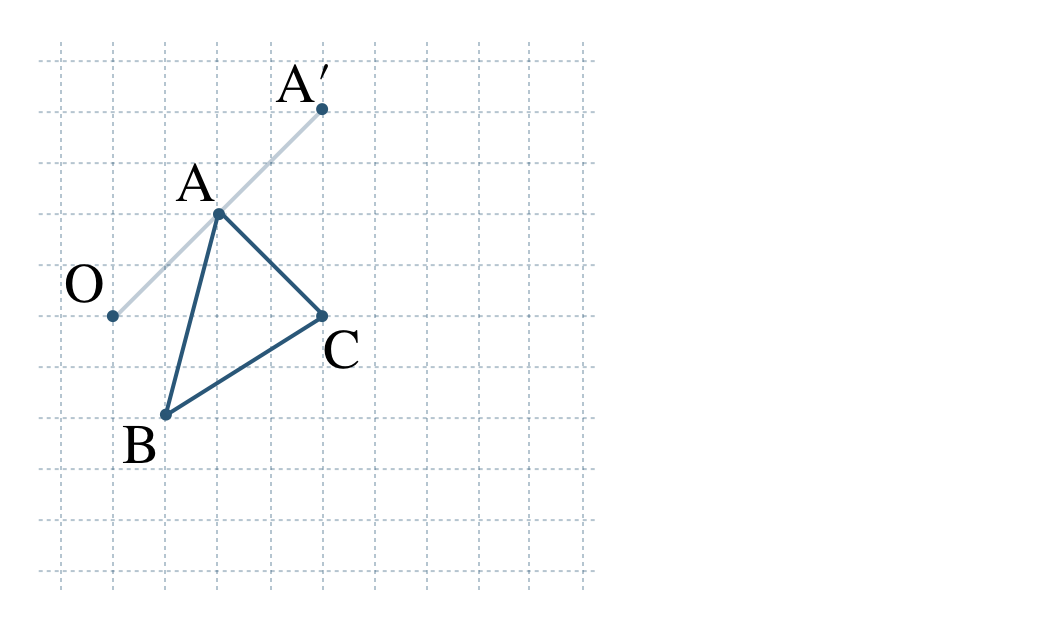
\({\small (2)}~\)次の図に、点 \({\rm O}\) を相似の中心として、\(\triangle {\rm ABC}\) を \(3\) 倍に拡大した \(\triangle {\rm A’B’C’}\) をかけ。
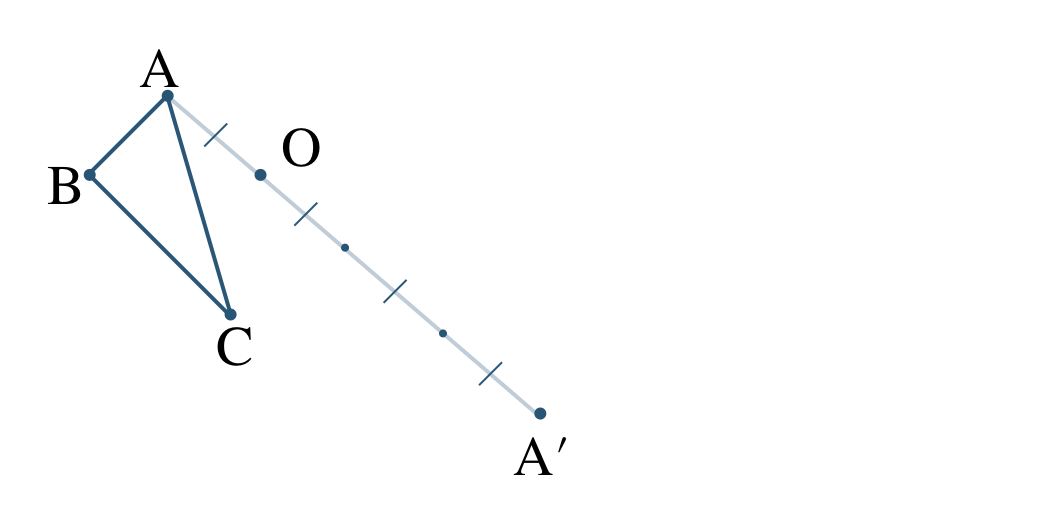
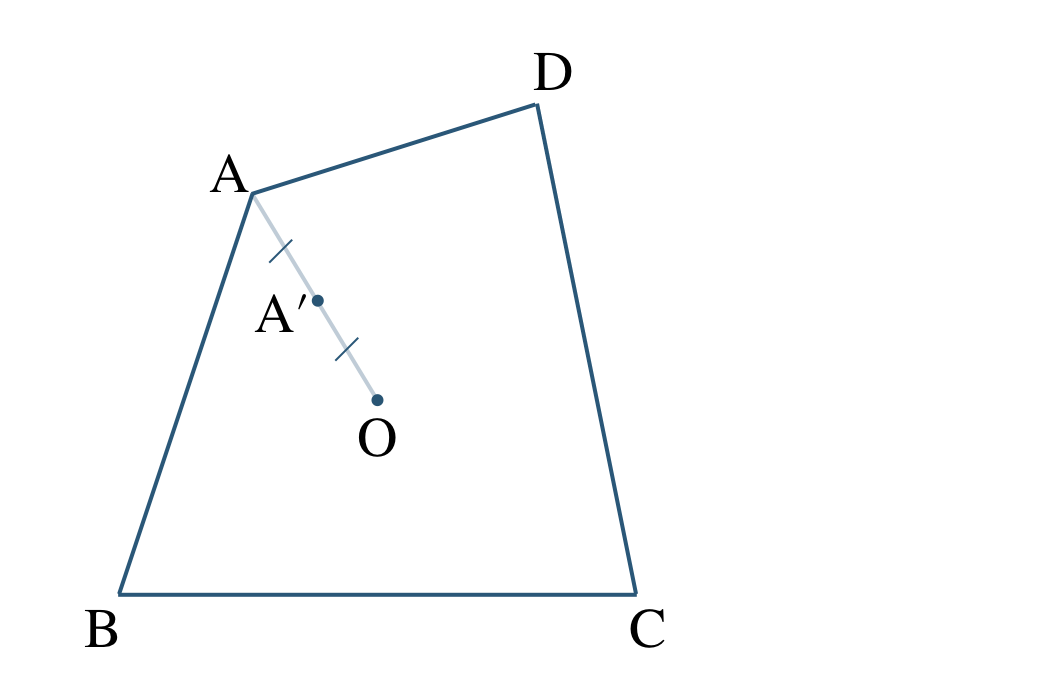
\({\small (3)}~\)次の図に、点 \({\rm O}\) を相似の中心として、四角形 \( {\rm ABCD}\) を \(\begin{split} \frac{\,1\,}{\,2\,}\end{split}\) 倍に縮小した四角形 \( {\rm A’B’C’D’}\) をかけ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
\({\small (2)}~\)

\({\small (3)}~\)


三角形の相似条件
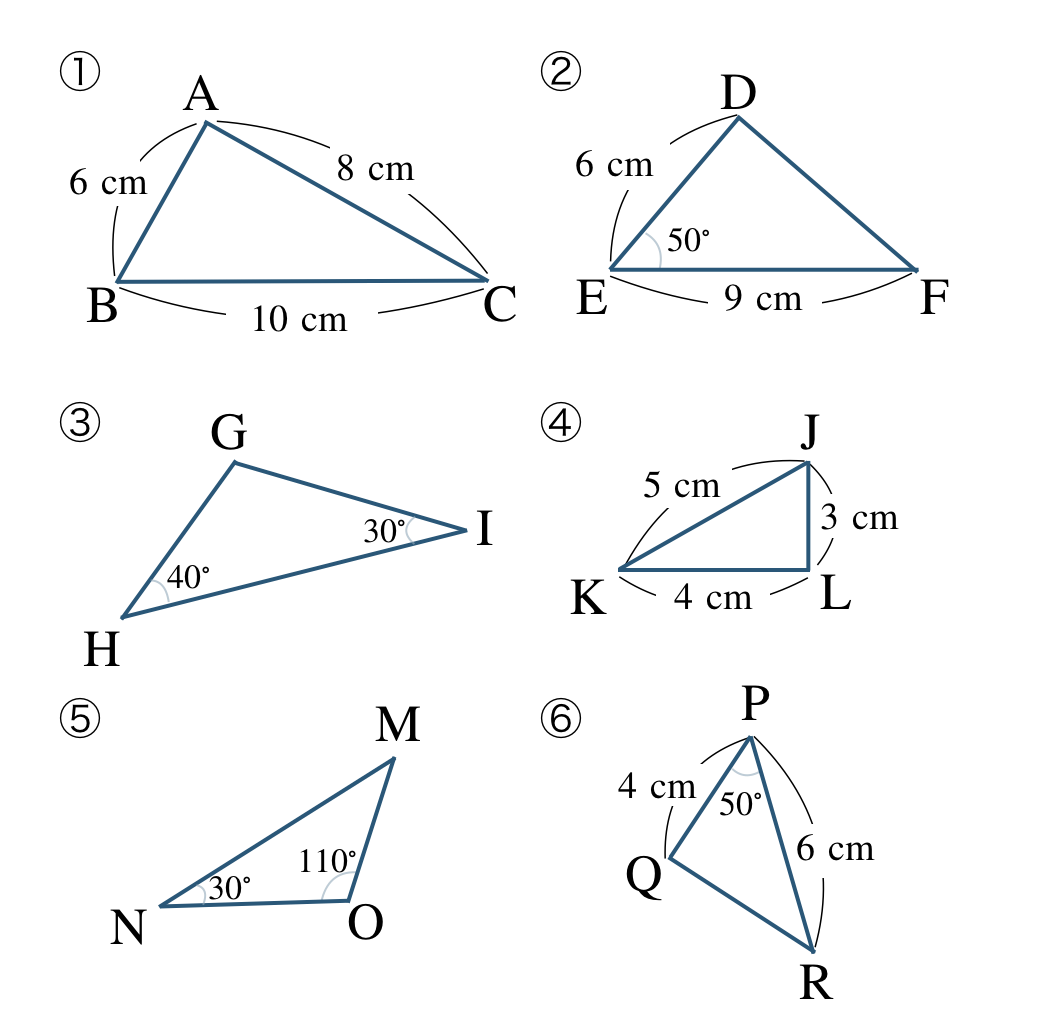
次の図において、相似な三角形を見つけて、記号を使って表せ。また、そのときの相似条件を答えよ。
[ 解答を見る ]
【解答】
①と④
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm LJK}\)
3組の辺の比がそれぞれ等しい
②と⑥
\(\triangle {\rm DEF}\,\,\unicode{x223D}\,\,\triangle {\rm QPR}\)
2組の辺の比とその間の角がそれぞれ等しい
③と⑤
\(\triangle {\rm GHI}\,\,\unicode{x223D}\,\,\triangle {\rm OMN}\)
2組の角がそれぞれ等しい

相似な三角形
次の図において、相似な三角形を見つけて、記号を使って表せ。また、そのときの相似条件を答えよ。
\({\small (1)}~\)
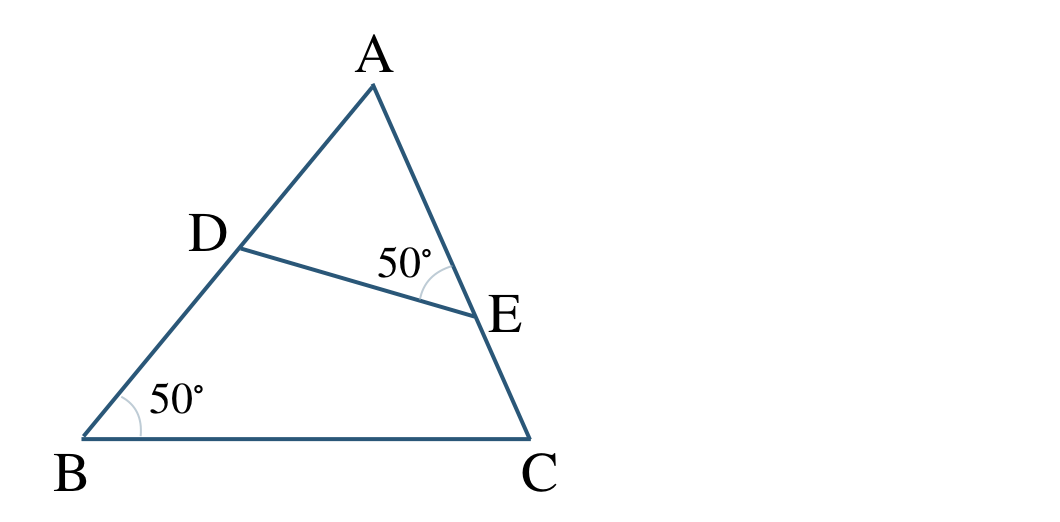
\({\small (2)}~\)
\({\small (3)}~\)

\({\small (4)}~\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm AED}\)
2組の角がそれぞれ等しい
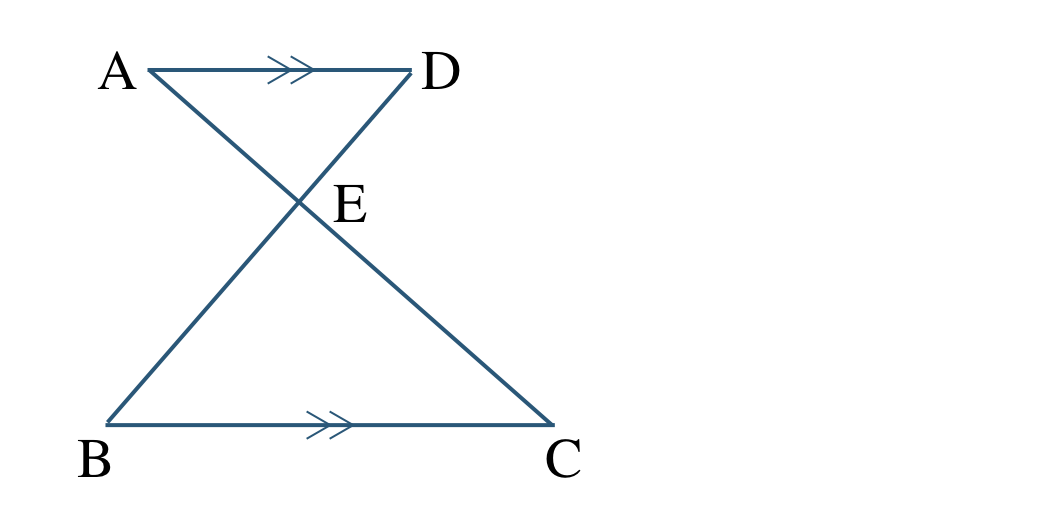
\({\small (2)}~\)\(\triangle {\rm AED}\,\,\unicode{x223D}\,\,\triangle {\rm CEB}\)
2組の角がそれぞれ等しい
\({\small (3)}~\)\(\triangle {\rm ABE}\,\,\unicode{x223D}\,\,\triangle {\rm DCE}\)
2組の辺の比とその間の角がそれぞれ等しい
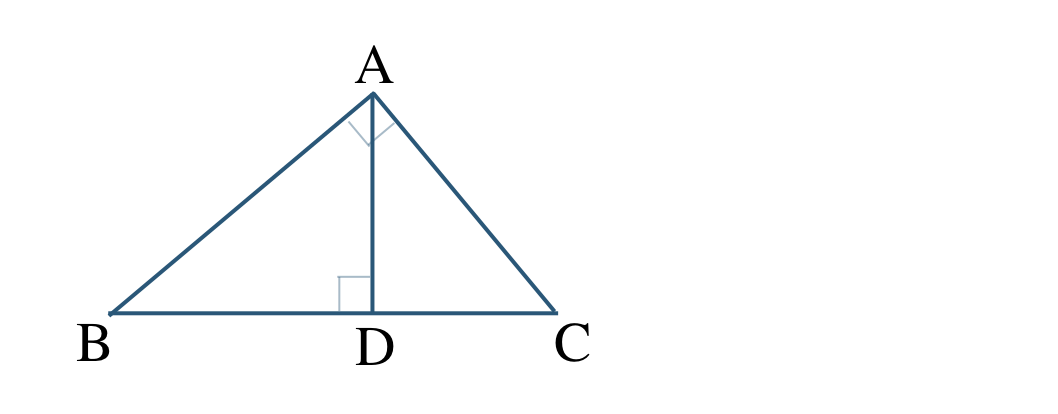
\({\small (4)}~\)\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm DBA}\)
2組の角がそれぞれ等しい
\(\triangle {\rm ABD}\,\,\unicode{x223D}\,\,\triangle {\rm CAD}\)
2組の角がそれぞれ等しい
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm DAC}\)
2組の角がそれぞれ等しい

相似の証明
次の証明をせよ。
\({\small (1)}~\)\({\rm BC\,//\,DE}\) のとき、\(\triangle {\rm ABC}\) と \(\triangle {\rm ADE}\) の相似を証明せよ。
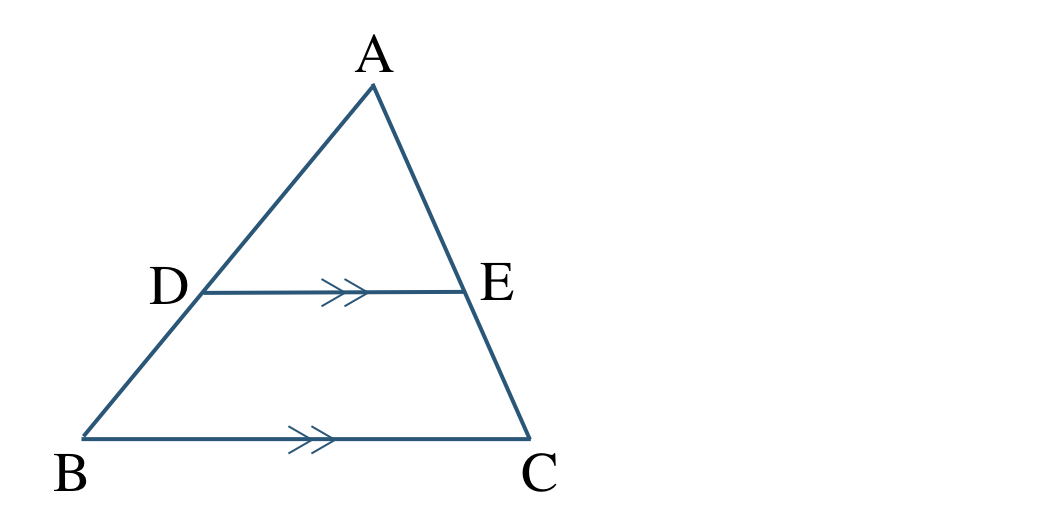
\({\small (2)}~\)\(\angle{\rm BAD}=\angle{\rm ACB}\) のとき、\(\triangle {\rm ABC}\) と \(\triangle {\rm DBA}\) の相似を証明せよ。
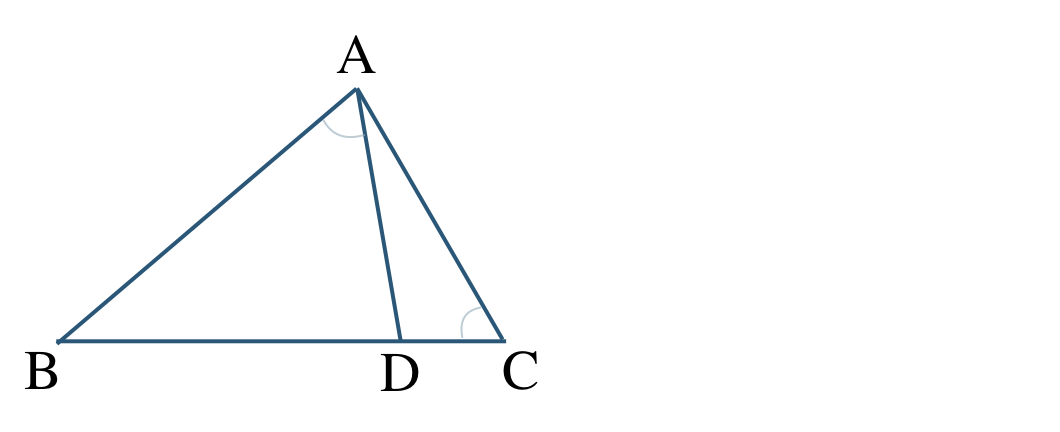
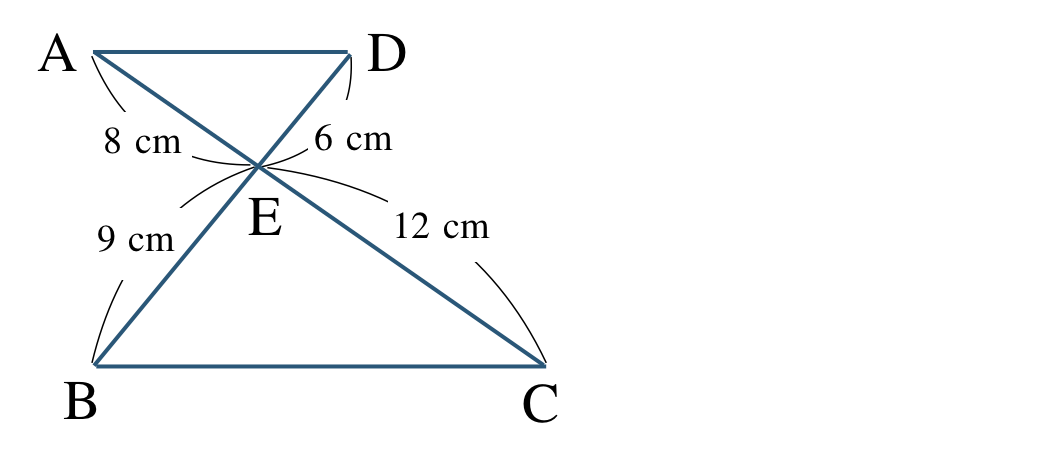
\({\small (3)}~\)\({\rm AD\,//\,BC}\) を証明せよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm ADE}\) において、
\({\rm A}\) が共通の角より、
\(\angle{\rm BAC}=\angle{\rm DAE}~~~\cdots{\large ①}\)
\({\rm BC\,//\,DE}\) より同位角が等しいから、
\(\angle{\rm ABC}=\angle{\rm ADE}~~~\cdots{\large ②}\)
①、②より、2組の角がそれぞれ等しいから
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm ADE}\)
[終]
\({\small (2)}~\)
[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm DBA}\) において、
仮定 \(\angle{\rm BAD}=\angle{\rm ACB}\) より、
\(\angle{\rm ACB}=\angle{\rm DAB}~~~\cdots{\large ①}\)
\({\rm B}\) が共通の角より、
\(\angle{\rm ABC}=\angle{\rm DBA}~~~\cdots{\large ②}\)
①、②より、2組の角がそれぞれ等しいから
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm DBA}\)
[終]
\({\small (3)}~\)
[証明] \(\triangle {\rm AED}\) と \(\triangle {\rm CEB}\) において、
仮定より、
\({\rm AE:CE}=8:12=2:3~~~\cdots{\large ①}\)
\({\rm DE:BE}=6:9=2:3~~~\cdots{\large ②}\)
対頂角が等しいから、
\(\angle{\rm AED}=\angle{\rm CEB}~~~\cdots{\large ③}\)
①、②、③より、2組の辺の比とその間の角がそれぞれ等しいから
\(\triangle {\rm AED}\,\,\unicode{x223D}\,\,\triangle {\rm CEB}\)
相似な図形では、対る角の大きさかわ等しいから、
\(\angle{\rm EAD}=\angle{\rm ECB}\)
錯角が等しいから、
\({\rm AD\,//\,BC}\)
[終]

三角形と線分の比
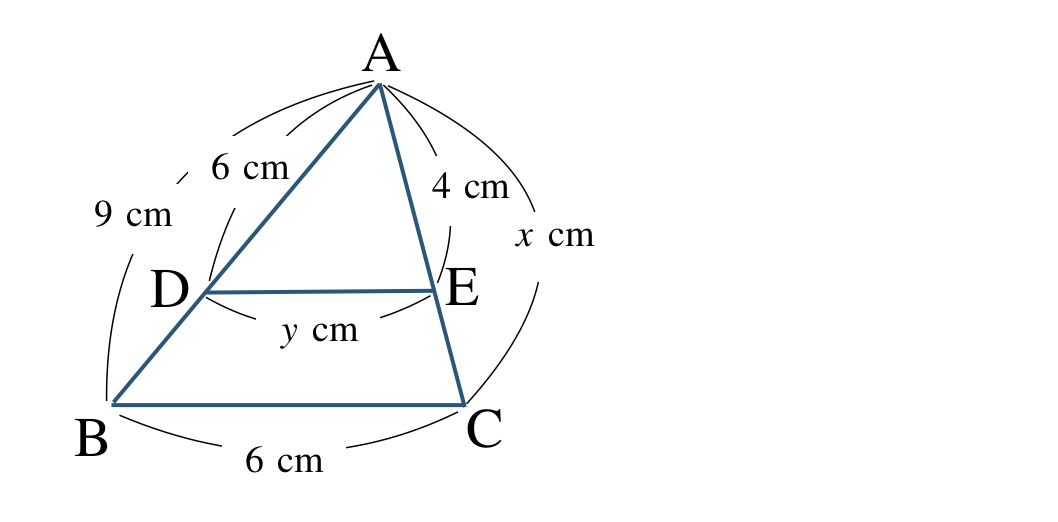
次の図で \({\rm BC\,//\,DE}\) のとき、\(x~,~y\) の値を求めよ。
\({\small (1)}~\)
\({\small (2)}~\)
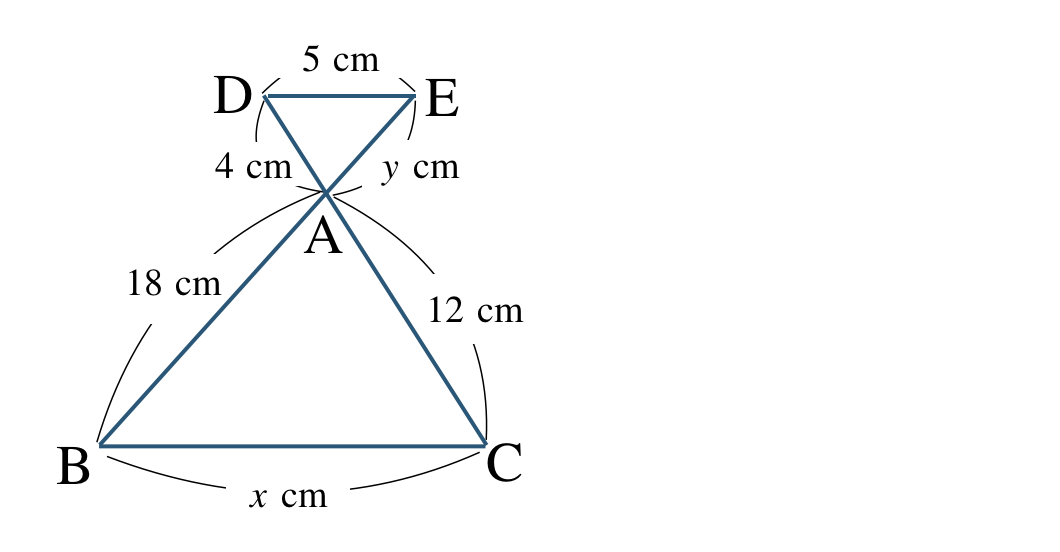
\({\small (3)}~\)
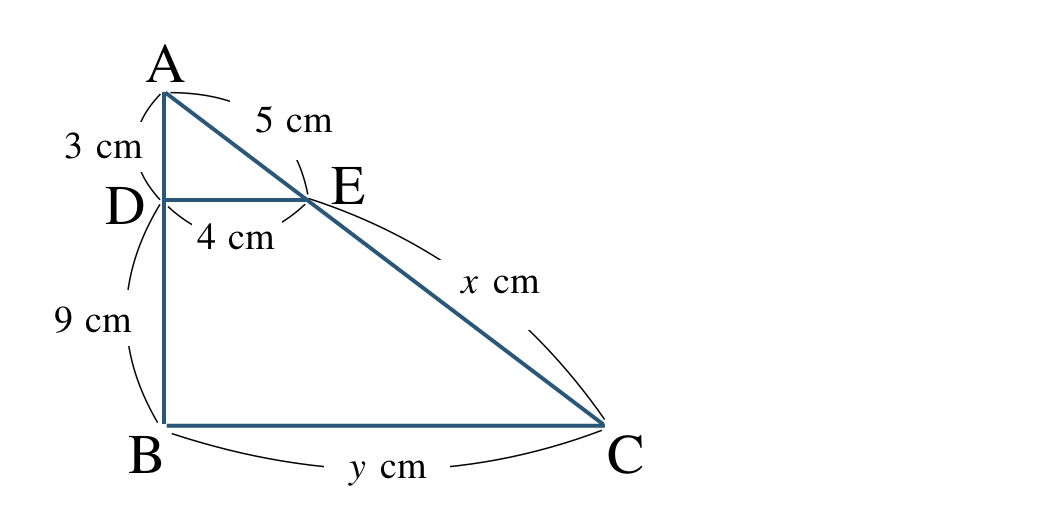
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(x=6~~{\rm cm}~,~y=4~~{\rm cm}\)
\({\small (2)}~\)\(x=15~~{\rm cm}~,~y=6~~{\rm cm}\)
\({\small (3)}~\)\(x=15~~{\rm cm}~,~y=16~~{\rm cm}\)

三角形の線分の比と平行線
次の問いに答えよ。
\({\small (1)}~\)次の \(\triangle {\rm ABC}\) において、
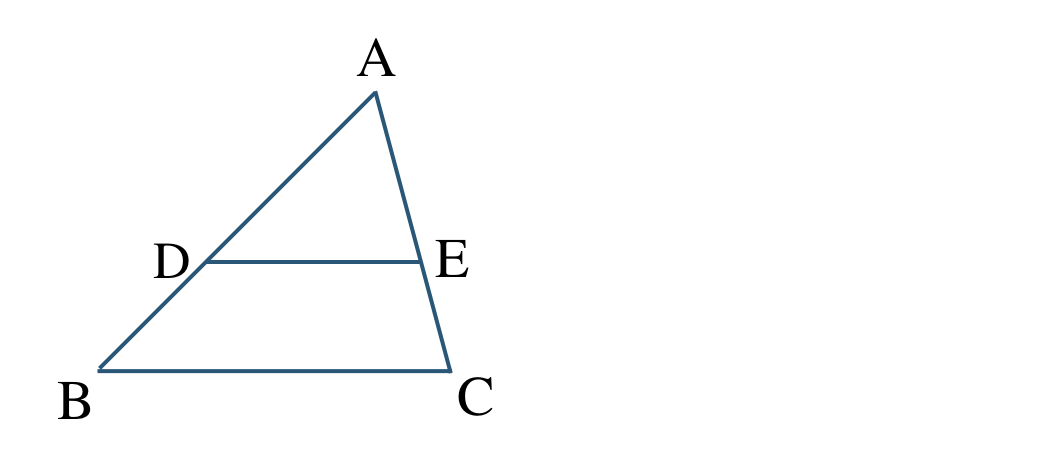
\({\rm AD:DB=AE:EC}=2:1\)
であるとき、次の問いに答えよ。
① \({\rm AD:AB}\) の比を求めよ。
② \({\rm BC}\) と \({\rm DE}\) の関係を答えよ。
③ \({\rm BC:DE}\) の比を求めよ。
\({\small (2)}~\)次の \(\triangle {\rm ABC}\) において、線分 \({\rm DE~,~EF~,~FD}\) のうち、\(\triangle {\rm ABC}\) の辺と平行であるものを答えよ。
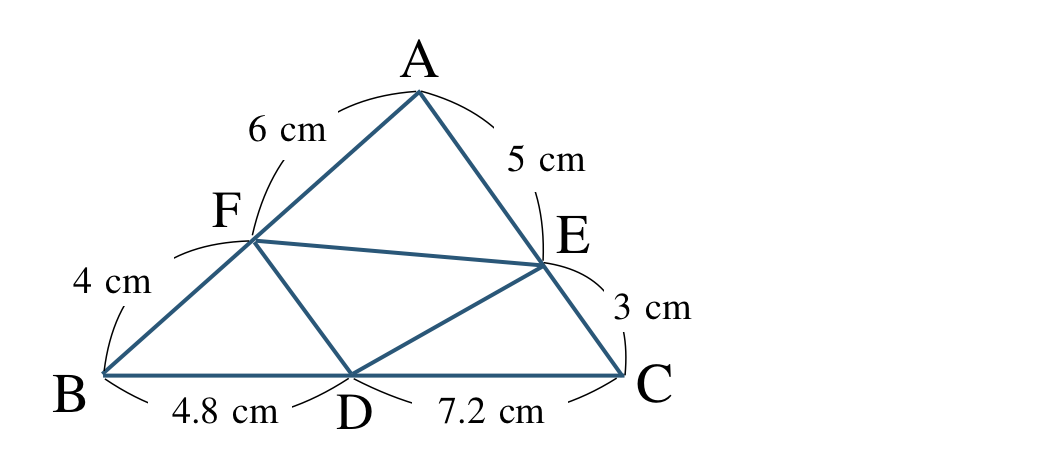
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \({\rm AD:AB}=2:3\)
② 線分 \({\rm BC}\) と \({\rm DE}\) は平行
③ \({\rm BC:DE}=3:2\)
\({\small (2)}~\)辺 \({\rm AC}\) と線分 \({\rm FD}\) が平行である

中点連結定理
次の問いに答えよ。
\({\small (1)}~\)次の \(\triangle {\rm ABC}\) において、点 \({\rm D~,~E}\) がそれぞれ辺 \({\rm AB~,~AC}\) の中点であるとき、
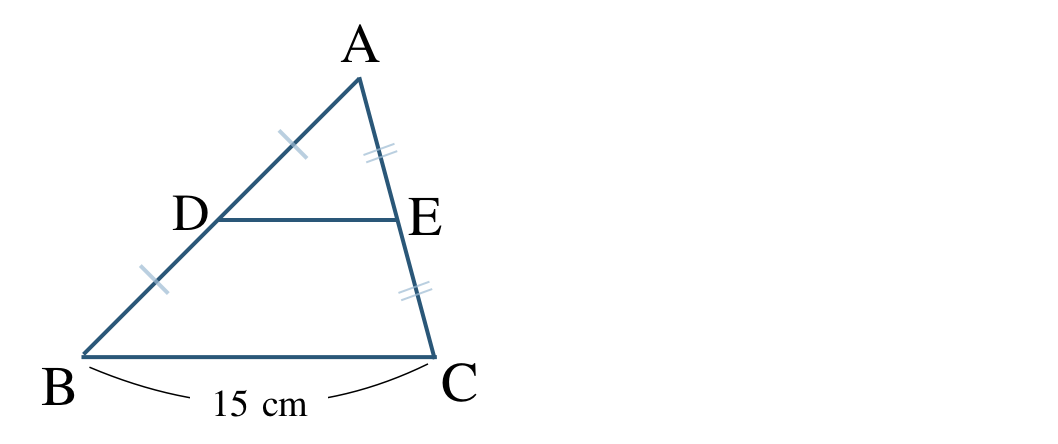
① 辺 \({\rm BC}\) と線分 \({\rm DE}\) の関係を答えよ。
② 線分 \({\rm DE}\) の長さを求めよ。
\({\small (2)}~\)次の \(\triangle {\rm ABC}\) において、点 \({\rm D~,~E~,~F}\) がそれぞれ辺 \({\rm AB~,~BC~,~AC}\) の中点であるとき、
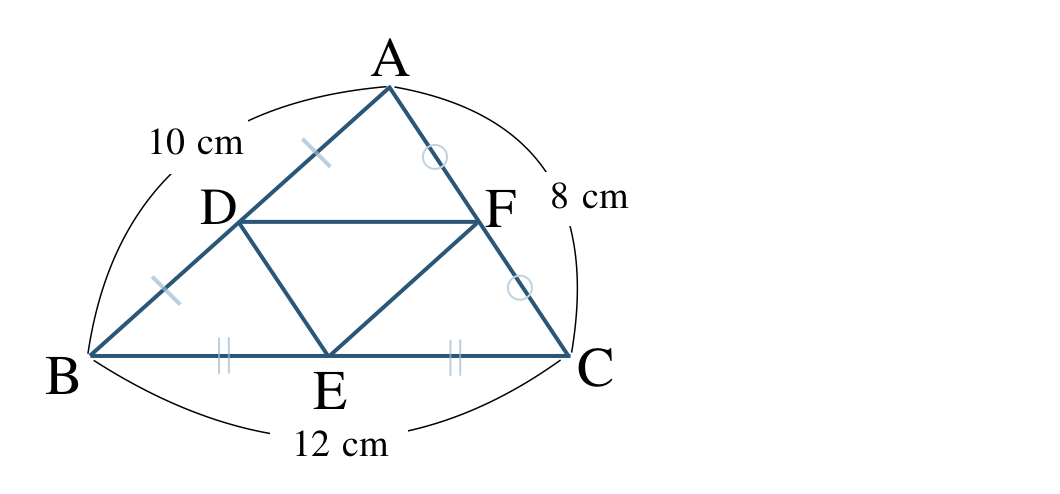
① \(\triangle {\rm DEF}\) の周の長さを求めよ。
② 合同な図形をすべて答えよ。
③ 相似である \(\triangle {\rm ABC}\) と \(\triangle {\rm EFD}\) の相似条件と相似比を求めよ。
\({\small (3)}~\)次の四角形 \({\rm ABCD}\) において、点 \({\rm E}\) は辺 \({\rm AB}\) の中点であり、線分 \({\rm AD}\) と \({\rm EF}\) と \({\rm BC}\) は平行である。また、対角線 \({\rm AC}\) と線分 \({\rm EF}\) の交点を \({\rm G}\) とすると、
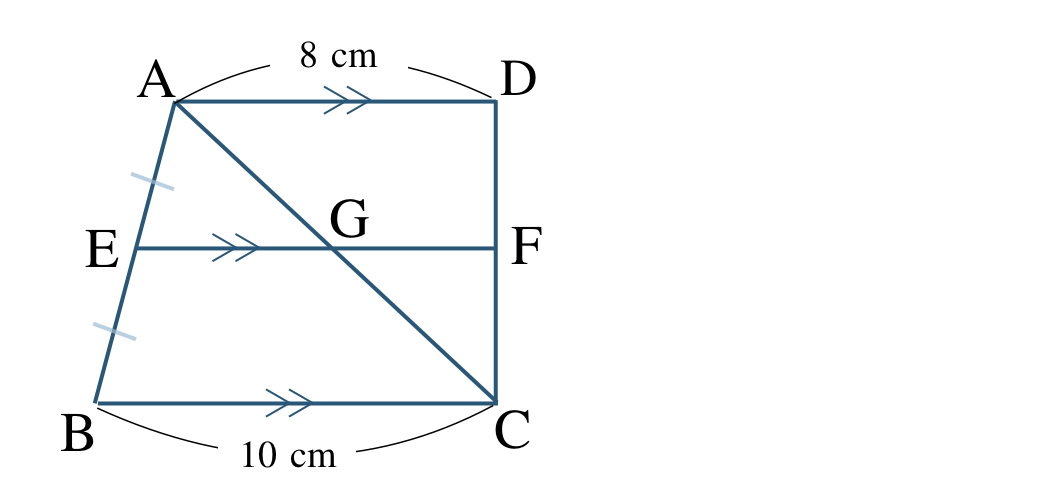
① \({\rm AG:GC}\) の比を求めよ。
② \({\rm CF:FD}\) の比を求めよ。
③ 線分 \({\rm EF}\) の長さを求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \({\rm DE\,//\,BC}\)
② \({\large \frac{\,15\,}{\,2\,}} ~{\rm cm}\)
\({\small (2)}~\)
① \({\rm DE\,//\,BC}\)\(15~{\rm cm}\)
② \(\triangle {\rm ADF}~,~\triangle {\rm DBE}~,~\triangle {\rm FEC}~,~\triangle {\rm EFD}\) が合同
③ 相似条件は、3組の辺の比がそれぞれ等しい
相似比は \(2:1\)
\({\small (3)}~\)
① \({\rm AG:GC=}1:1\)
② \({\rm CF:FD=}1:1\)
③ \(9~~{\rm cm}\)

中点連結定理の利用
次の問いに答えよ。
\({\small (1)}~\)次の四角形 \({\rm ABCD}\) について、点 \({\rm E~,~F~,~G~,~H}\) がそれぞれ辺 \({\rm AB~,~BC~,~CD~,~DA}\) の中点であるとき、
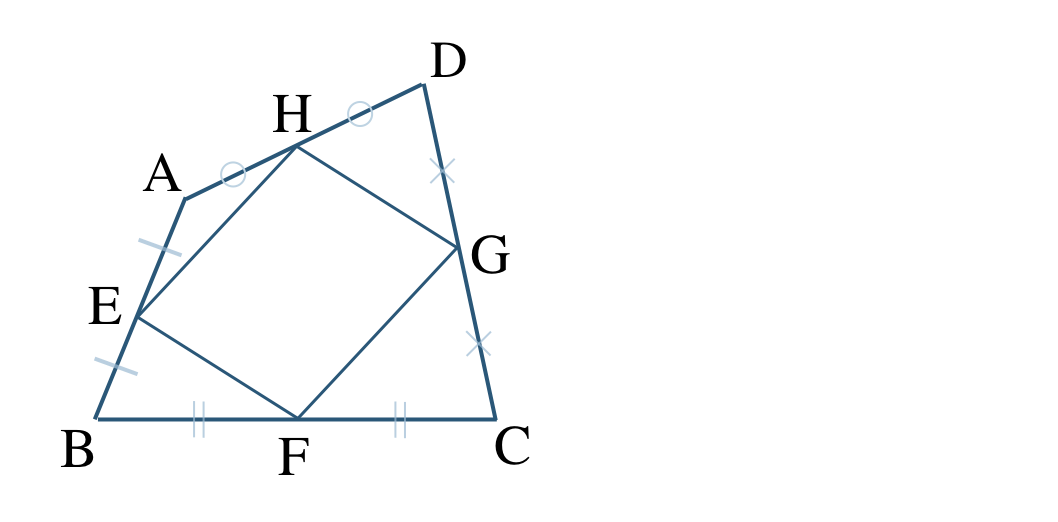
① 四角形 \({\rm EFGH}\) が平行四辺形であることを証明せよ。
② \({\rm AC=BD}\) のとき、四角形 \({\rm EFGH}\) はどのような四角形となるか答えよ。
③ 四角形 \({\rm ABCD}\) が長方形のとき、四角形 \({\rm EFGH}\) はどのような四角形となるか答えよ。
④ 四角形 \({\rm ABCD}\) がひし形のとき、四角形 \({\rm EFGH}\) はどのような四角形となるか答えよ。
\({\small (2)}~\)次の四角形 \({\rm ABCD}\) について、点 \({\rm E~,~F}\) がそれぞれ辺 \({\rm AB~,~CD}\) の中点で、点 \({\rm P~,~Q}\) がそれぞれ対角線 \({\rm BD~,~AC}\) の中点であるとき、
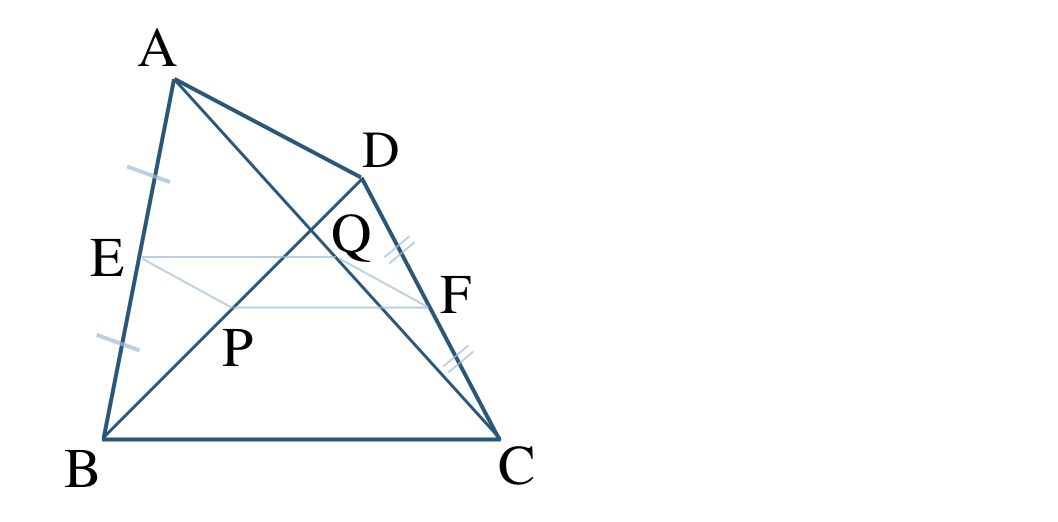
① 四角形 \({\rm EPFQ}\) が平行四辺形であることを証明せよ。
② \({\rm AD=BC}\) のとき、四角形 \({\rm EPFQ}\) はどのような四角形となるか答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① [証明] 対角線 \({\rm AC}\) を引くと、
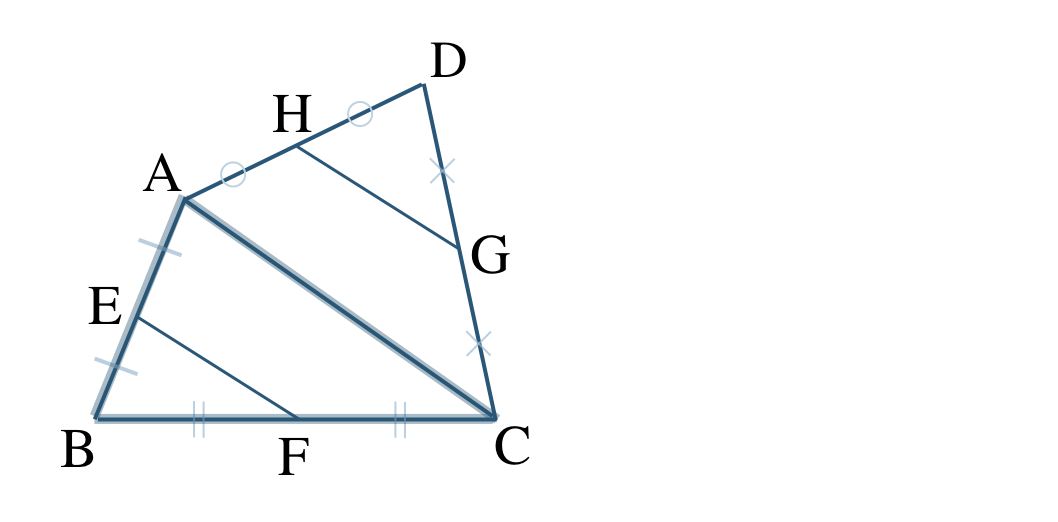
\(\triangle {\rm ABC}\) において、点 \({\rm E~,~F}\)はそれぞれ辺 \({\rm AB~,~BC}\) の中点であるので、中点連結定理より、$$~~~{\rm EF\,//\,AC}~,~{\rm EF}=\frac{\,1\,}{\,2\,}{\rm AC}$$また、\(\triangle {\rm DAC}\) において、点 \({\rm H~,~G}\)はそれぞれ辺 \({\rm AD~,~CD}\) の中点であるので、中点連結定理より、$$~~~{\rm HG\,//\,AC}~,~{\rm HG}=\frac{\,1\,}{\,2\,}{\rm AC}$$
よって、\({\rm EF\,//\,AC}\) と \({\rm HG\,//\,AC}\) より、$$~~~{\rm EF\,//\,HG}$$\({\rm EF={\large \frac{\,1\,}{\,2\,}}AC}\) と \({\rm HG={\large \frac{\,1\,}{\,2\,}}AC}\) より、$$~~~{\rm EF=HG}$$これより、1組の対辺が等しくて平行であるので、
四角形 \({\rm EFGG}\) は平行四辺形である
[終]
② 四角形 \({\rm EFGH}\) はひし形
③ 四角形 \({\rm EFGH}\) はひし形
④ 四角形 \({\rm EFGH}\) は長方形
\({\small (2)}~\)
① [証明]\(\triangle {\rm ABC}\) において、
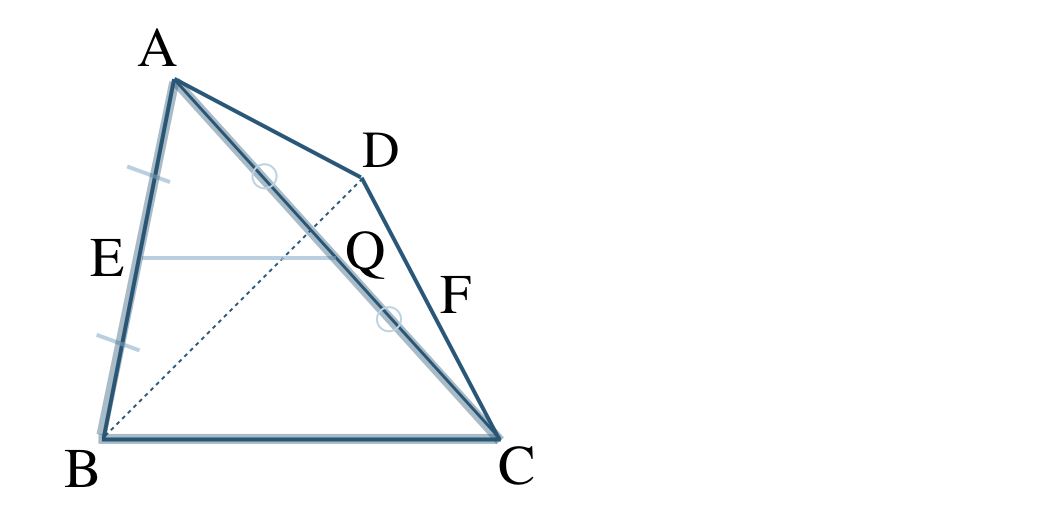
点 \({\rm E~,~Q}\)はそれぞれ辺 \({\rm AB~,~AC}\) の中点であるので、中点連結定理より、$$~~~{\rm EQ\,//\,BC}~,~{\rm EQ}=\frac{\,1\,}{\,2\,}{\rm BC}$$また、\(\triangle {\rm DBC}\) において、
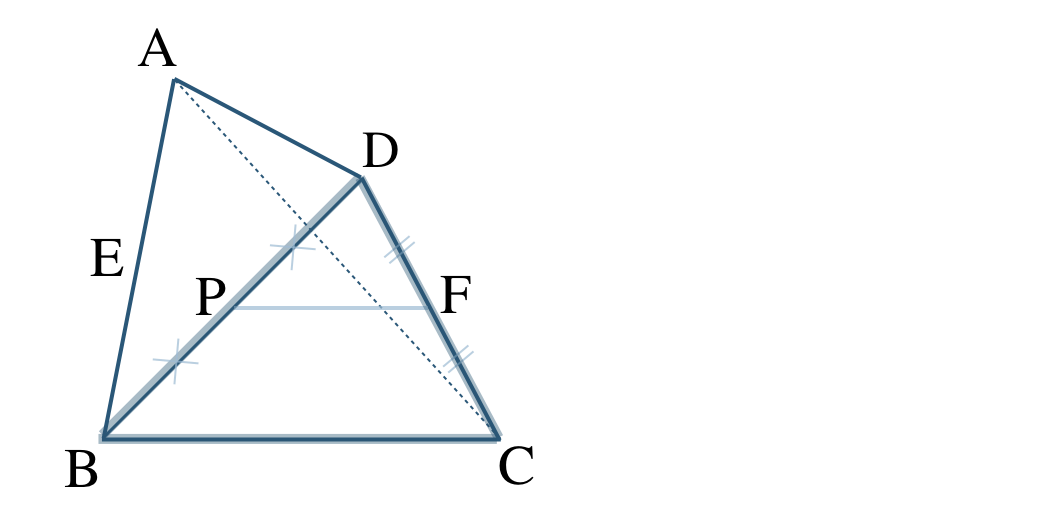
点 \({\rm P~,~F}\)はそれぞれ辺 \({\rm DB~,~DC}\) の中点であるので、中点連結定理より、$$~~~{\rm PF\,//\,BC}~,~{\rm PF}=\frac{\,1\,}{\,2\,}{\rm BC}$$
よって、\({\rm EQ\,//\,BC}\) と \({\rm PF\,//\,BC}\) より、$$~~~{\rm EQ\,//\,PF}$$\({\rm EQ={\large \frac{\,1\,}{\,2\,}}BC}\) と \({\rm PF={\large \frac{\,1\,}{\,2\,}}BC}\) より、$$~~~{\rm EQ=PF}$$これより、1組の対辺が等しくて平行であるので、
四角形 \({\rm EPFQ}\) は平行四辺形である
[終]
② 四角形 \({\rm EPFQ}\) はひし形

平行線と線分の比
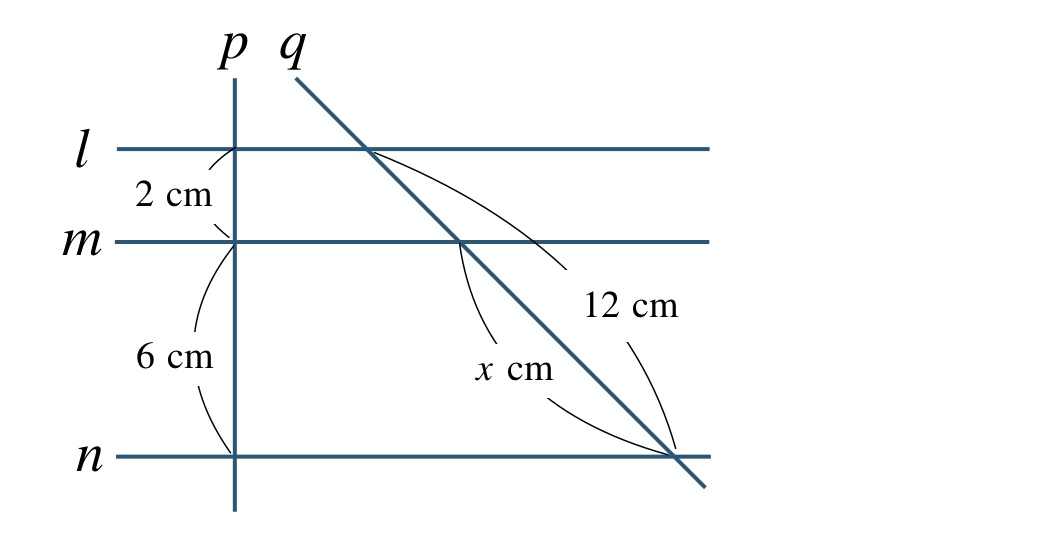
次の図で \(l\,//\,m\,//\,n\) であるとき、\(x\) の値を求めよ。
\({\small (1)}~\)
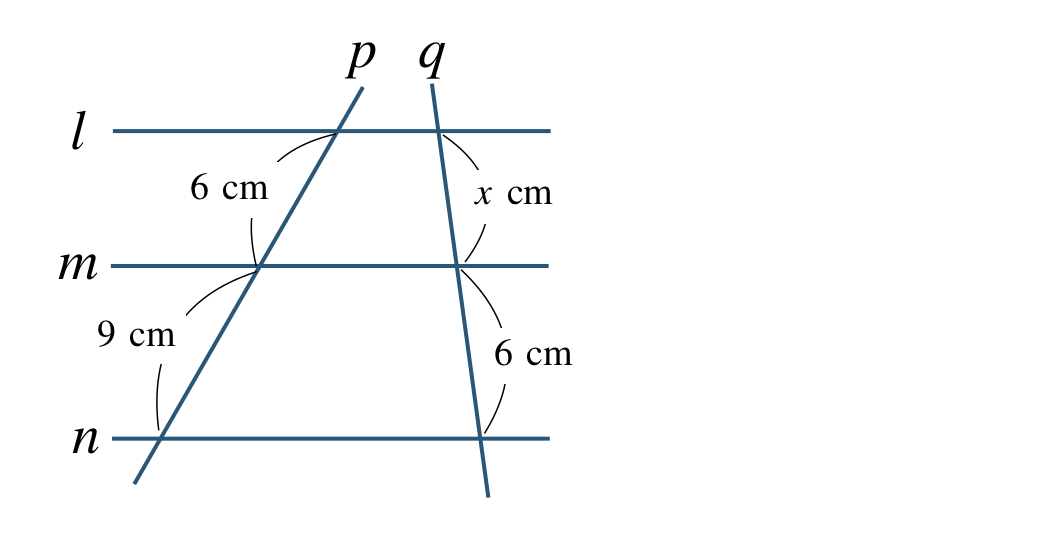
\({\small (2)}~\)
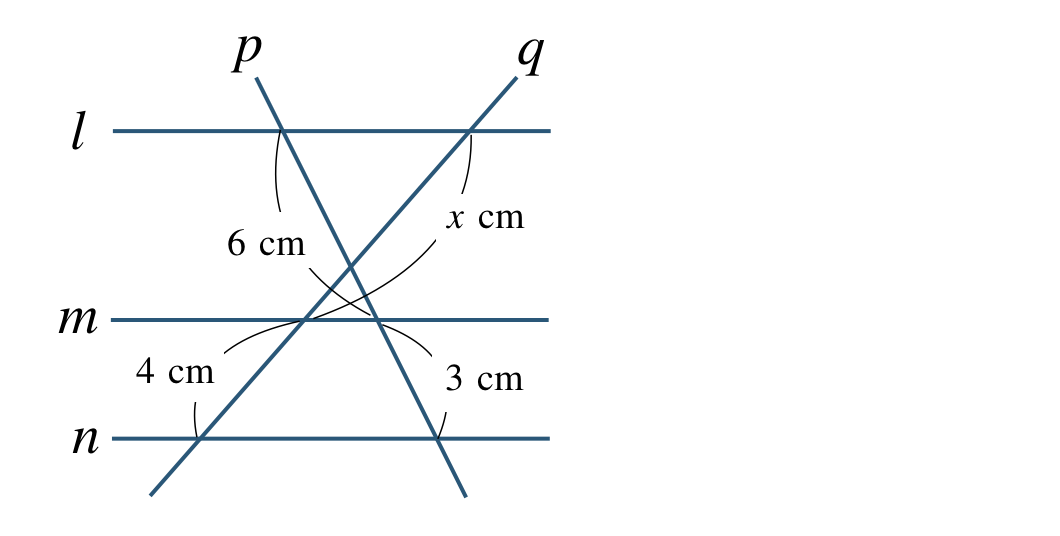
\({\small (3)}~\)
[ 解答を見る ]
【解答】
\({\small (1)}~x=4~{\rm cm}\)
\({\small (2)}~x=8~{\rm cm}\)
\({\small (3)}~x=9~{\rm cm}\)

角の二等分線と比
次の問いに答えよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) の \(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とするとき、
\({\rm AB:AC=BD:DC}\)
を証明せよ。
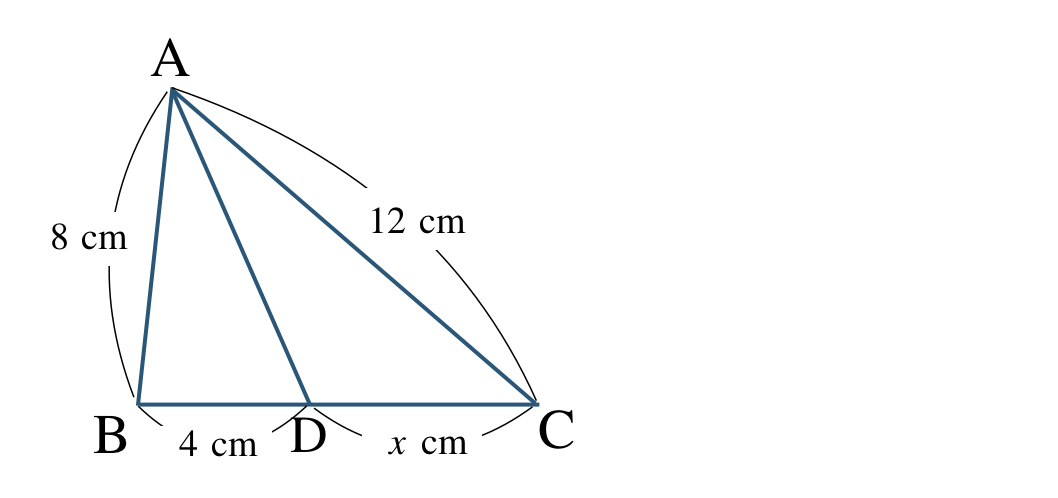
\({\small (2)}~\)線分 \({\rm AD}\) は \(\angle {\rm BAC}\) の二等分線であるとき、\(x\) の値を求めよ。
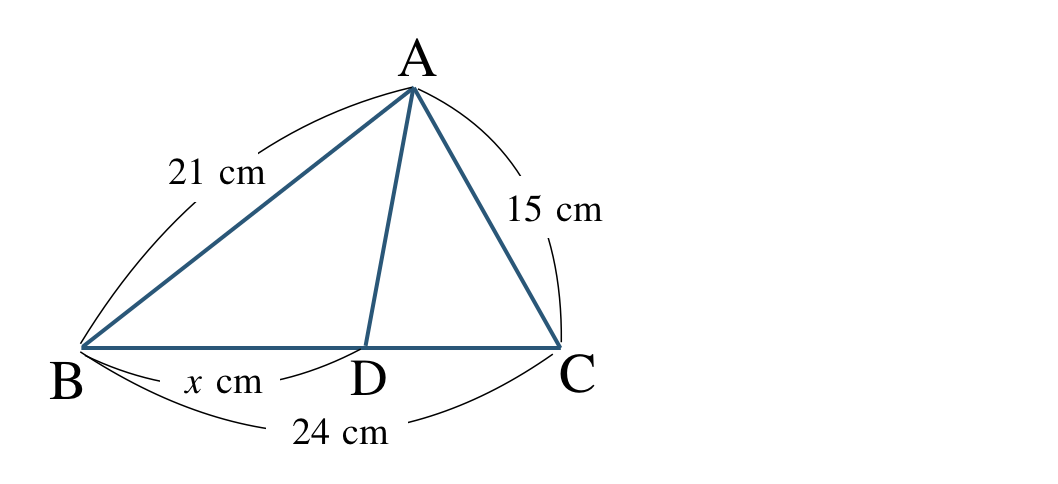
\({\small (3)}~\)線分 \({\rm AD}\) は \(\angle {\rm BAC}\) の二等分線であるとき、\(x\) の値を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)[証明]
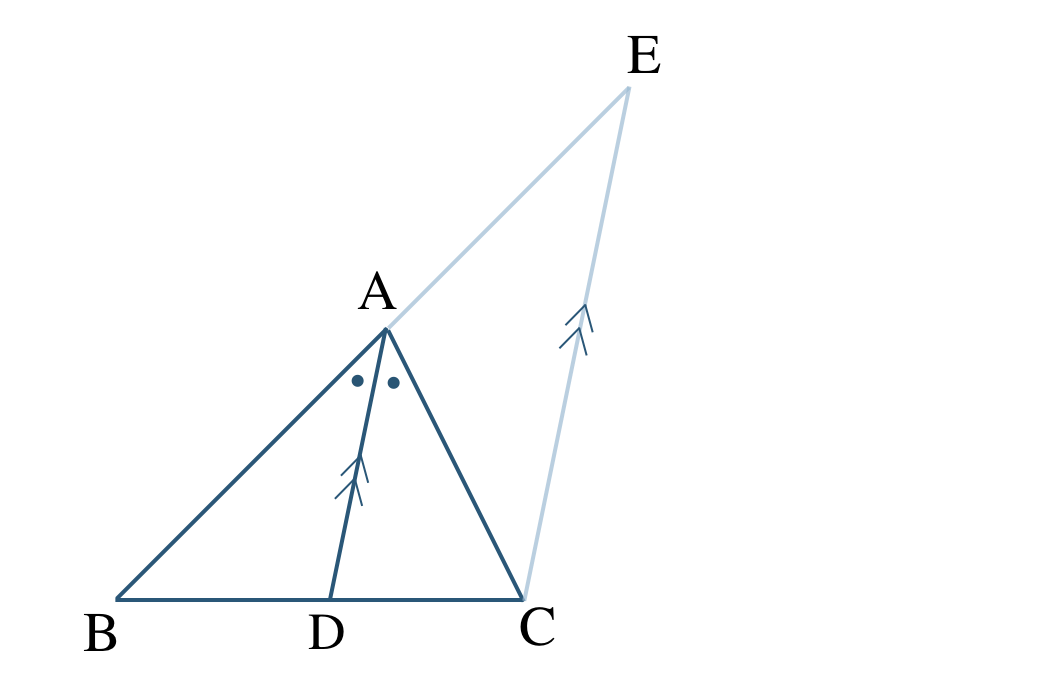
点 \({\rm C}\) を通り線分 \({\rm DA}\) に平行な直線と、辺 \({\rm AB}\) の延長線との交点を \({\rm E}\) とする
\({\rm AD\,//\,EC}\) より、同位角が等しいので、
\(\angle{\rm BAD}=\angle{\rm AEC}\)
\({\rm AD\,//\,EC}\) より、錯角が等しいので、
\(\angle{\rm DAC}=\angle{\rm ACE}\)
また、仮定より、
\(\angle{\rm BAD}=\angle{\rm DAC}\)
よって、
\(\angle{\rm AEC}=\angle{\rm ACE}\)
\(\triangle {\rm ACE}\) は二等辺三角形となり、
\({\rm AC=AE}~~\cdots{\large ①}\)
また、\(\triangle {\rm BEC}\) において、\({\rm AD\,//\,EC}\) であるので、三角形の線分の比の定理より、
\({\rm BA:AE=BD:DC}~~\cdots{\large ②}\)
①、②より、
\({\rm AB:AC=BD:DC}\)
[終]
\({\small (2)}~x=6~{\rm cm}\)
\({\small (3)}~x=14~{\rm cm}\)

相似な図形の面積比
次の問いに答えよ。
\({\small (1)}~\)半径 \(6~{\rm cm}\) の円Aと半径 \(12~{\rm cm}\) の円Bにおいて、
① 相似比を求めよ。
② 面積比を求めよ。
\({\small (2)}~\)次の \(\triangle {\rm ABC}\) と \(\triangle {\rm ABC}\) が相似であるとき、
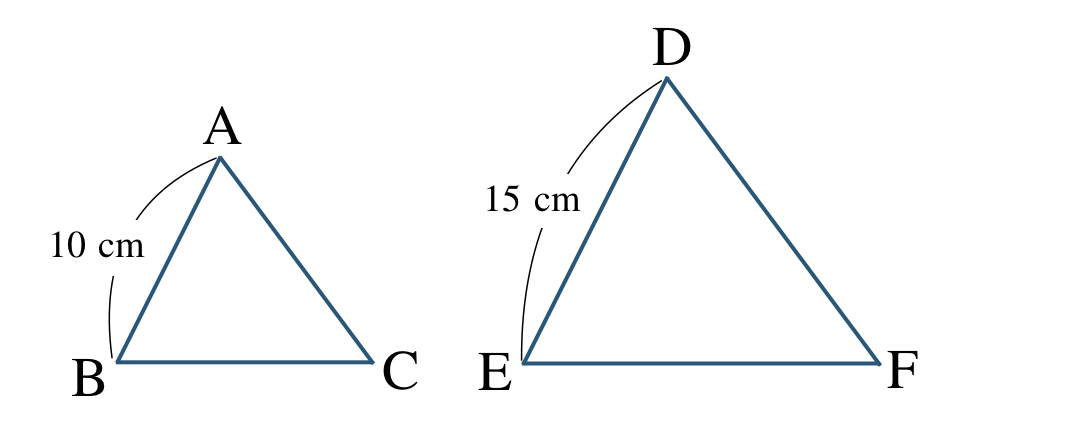
① 相似比を求めよ。
② 面積比を求めよ。
③ \(\triangle {\rm ABC}\) の面積が \(60~{\rm cm}^2\) のとき、\(\triangle {\rm DEF}\) の面積を求めよ。
\({\small (3)}~\)次の \(\triangle {\rm ABC}\) について、
\({\rm AD:DF:FB=2:1:1}\)
\({\rm BC\,//\,DE\,//\,FG}\)
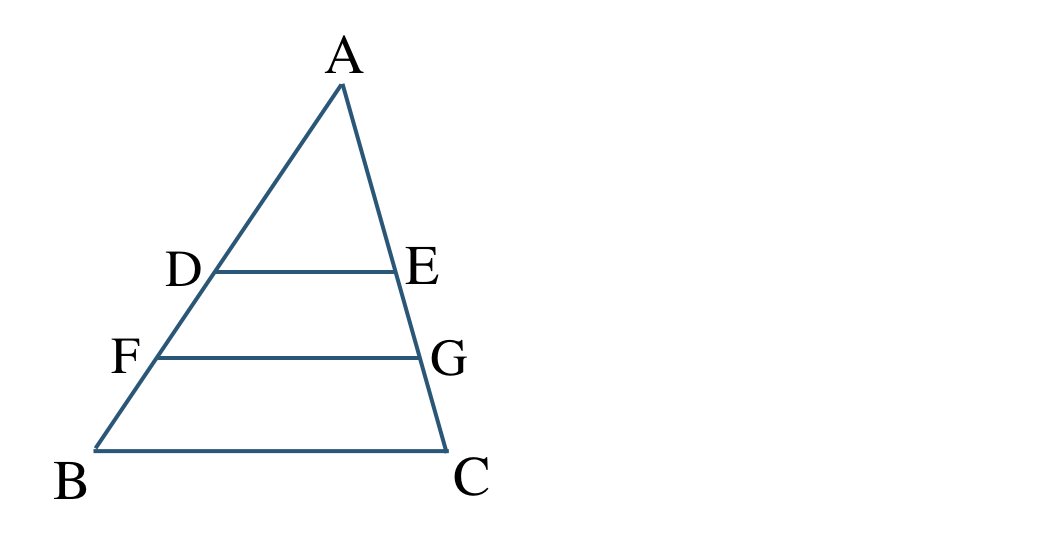
① \(\triangle {\rm ABC}\) と \(\triangle {\rm ADE}\) の面積比を求めよ。
② \(\triangle {\rm ABC}\) と \(\triangle {\rm AFG}\) の面積比を求めよ。
③ 台形 \({\rm DFGE}\) と台形 \({\rm FBCG}\) の面積比を求めよ。
\({\small (4)}~\)次の図形の面積比を求めよ。
① \(\triangle {\rm ABC}\) と \(\triangle {\rm DBC}\)
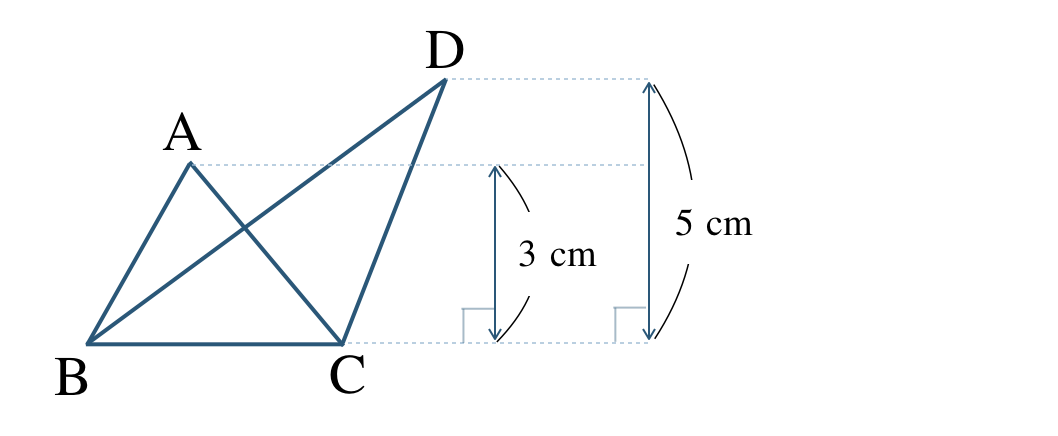
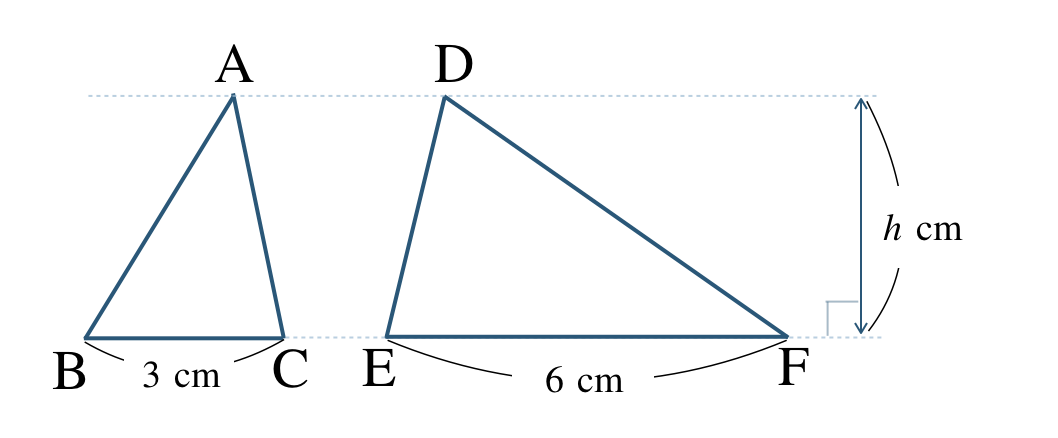
② \(\triangle {\rm ABC}\) と \(\triangle {\rm DEF}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(1:2\) ② \(1:4\)
\({\small (2)}~\)
① \(2:3\) ② \(4:9\)
③ \(135~{\rm cm}^2\)
\({\small (3)}~\)
① \(4:1\) ② \(16:9\)
③ \(5:7\)
\({\small (4)}~\)
① \(3:5\) ② \(1:2\)

相似な立体の表面積比と体積比
次の問いに答えよ。
\({\small (1)}~\)半径 \(6~{\rm cm}\) の球Aと半径 \(10~{\rm cm}\) の球Bについて、
① 相似比を求めよ。
② 表面積比を求めよ。
③ 体積比を求めよ。
\({\small (2)}~\)相似な2つの立体P、Qについて、相似比が \(7:2\) であるとき、
① Pの表面積が \(147~{\rm cm}^2\) であるとき、Qの表面積を求めよ。
② Qの体積が \(40~{\rm cm}^3\) であるとき、Pの体積を求めよ。
\({\small (3)}~\)次の図の円すいを高さで2等分するように分けたとき、上の円すいをA、下の立体をBとすると、
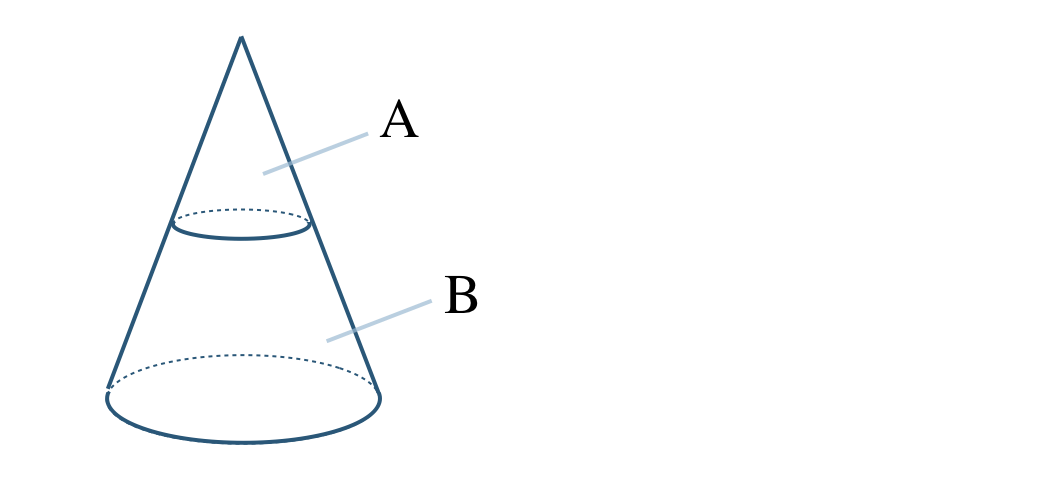
① もとの円すいと円すいAの体積比を求めよ。
② 円すいAと立体Bの体積比を求めよ。
③ もとの円すいの体積が \(96\pi~{\rm cm}^3\) のとき、立体Bの体積を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(3:5\) ② \(9:25\)
③ \(27:125\)
\({\small (2)}~\)
① \(12~{\rm cm}^2\) ② \(1715~{\rm cm}^3\)
\({\small (3)}~\)
① \(8:1\) ② \(1:7\)
③ \(84\pi~{\rm cm}^3\)

相似の利用
次の問いに答えよ。
\({\small (1)}~\)あるピザの値段は、ピザの面積に比例する。
直径 \(16~{\rm cm}\) のSサイズのピザが \(1200\) 円のとき、
① 直径 \(24~{\rm cm}\) のMサイズのピザの値段を求めよ。
② 直径 \(28~{\rm cm}\) のLサイズのピザの値段を求めよ。
\({\small (2)}~\)次の図のように、高さ \(10~{\rm cm}\) の円すいの容器に、高さ \(6~{\rm cm}\) まで水が入っている。容器と水の入った部分は相似である。
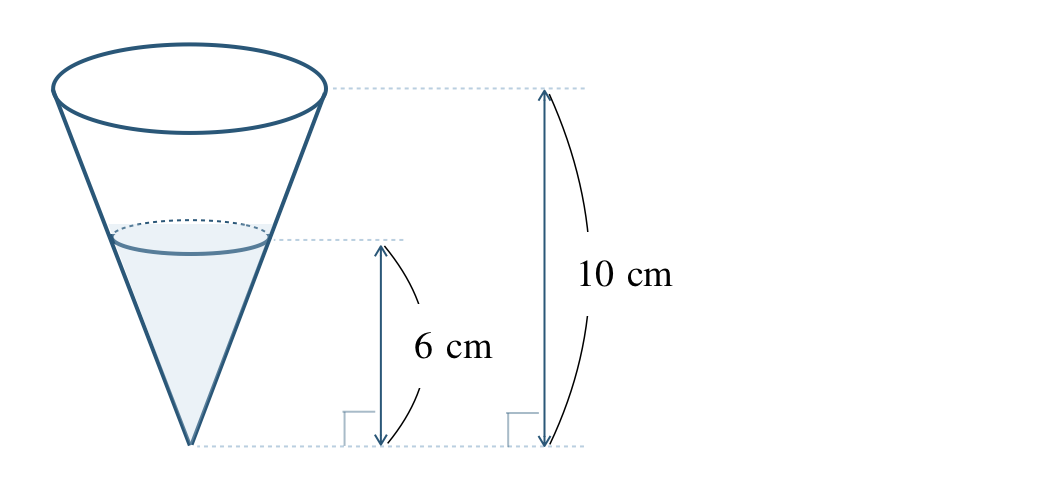
① 容器と水の入った部分の相似比を求めよ。
② 容器が容積 \(1000~{\rm cm}^3\) のとき、入っている水の体積を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(2700\) 円 ② \(3675\) 円
\({\small (2)}~\)
① \(5:3\) ② \(216~{\rm cm}^2\)

縮図の利用
次の問いに答えよ。
\({\small (1)}~\)図1はビルから \(10~{\rm m}\) 離れた地点 \({\rm A}\) からビルの上を見上げたもので、図2は図1の \({\large \frac{\,1\,}{\,500\,}}\) の縮図である。目の高さが \(1.5~{\rm m}\) であるとき、ビルの高さを求めよ。
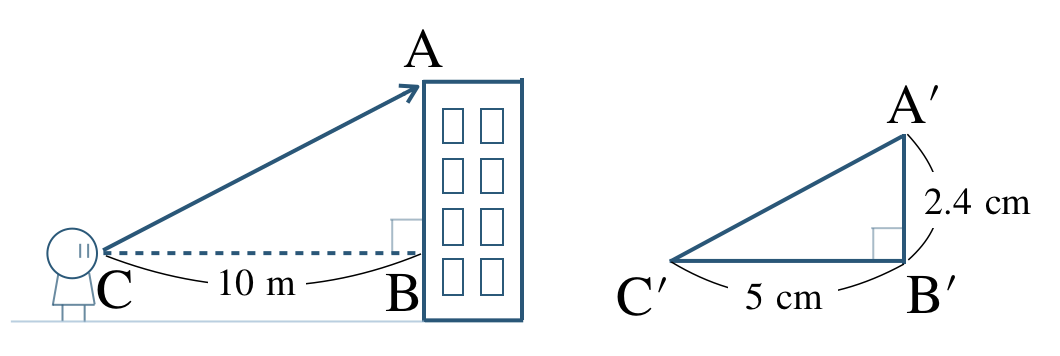
\({\small (2)}~\)次の図のような池がある。この \(\triangle {\rm ABC}\) の \({\large \frac{\,1\,}{\,200\,}}\) の縮図をかくことで、2点 \({\rm A~,~B}\) の距離を求めよ。
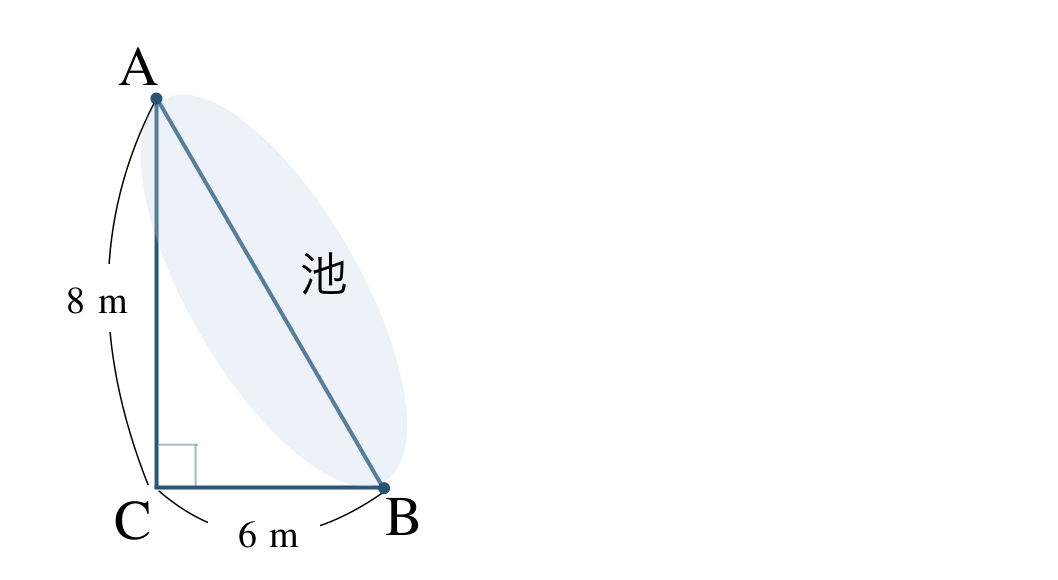
[ 解答を見る ]
【解答】
\({\small (1)}~\)ビルの高さ \(6.3~{\rm m}\)
\({\small (2)}~\)2点 \({\rm A~,~B}\) の距離は \(10~{\rm m}\)



