このページは「中学数学1 空間図形」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学1 空間図形
いろいろな立体
次の問いに答えよ。
\({\small (1)}~\)次の①〜⑧の立体の名前を答えよ。また、多面体であるものを選べ。
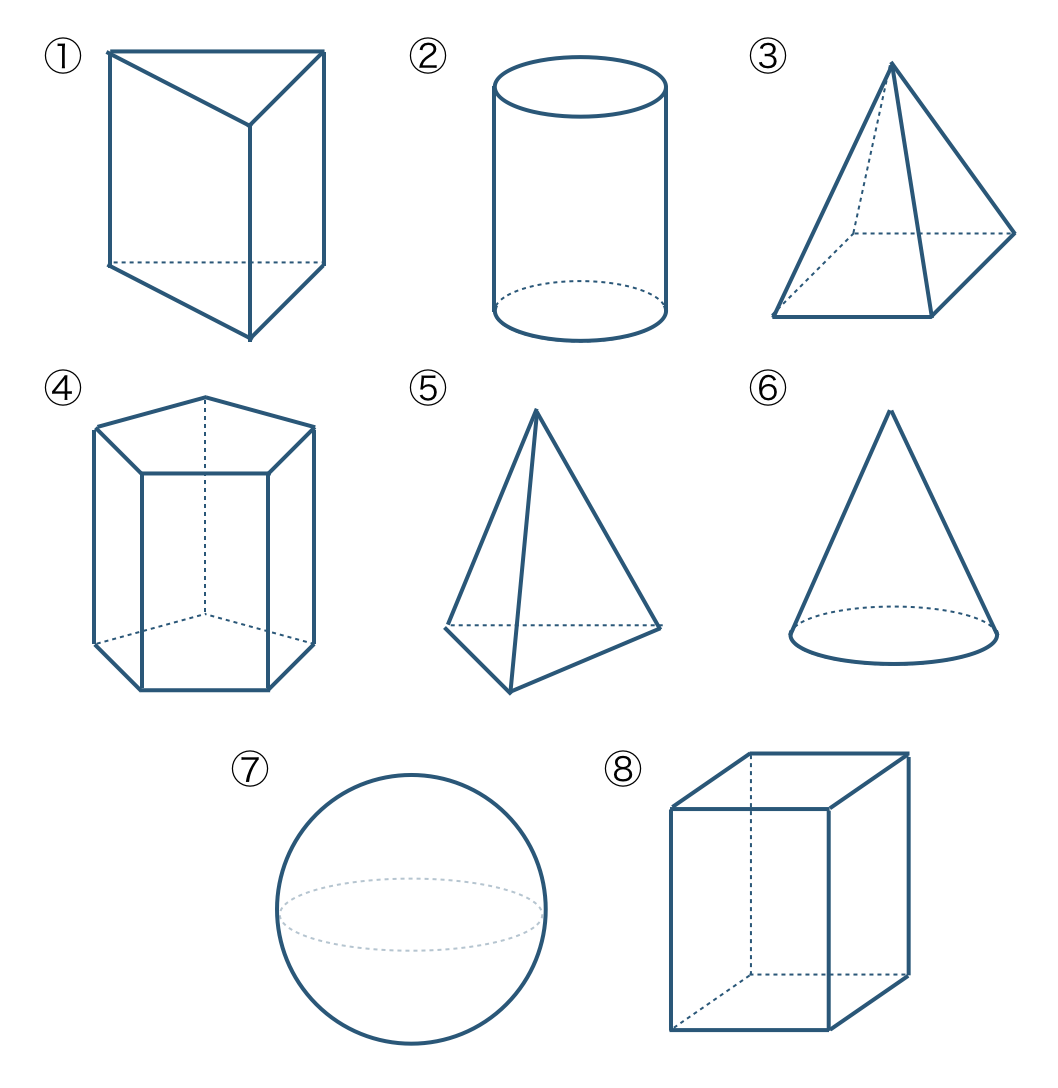
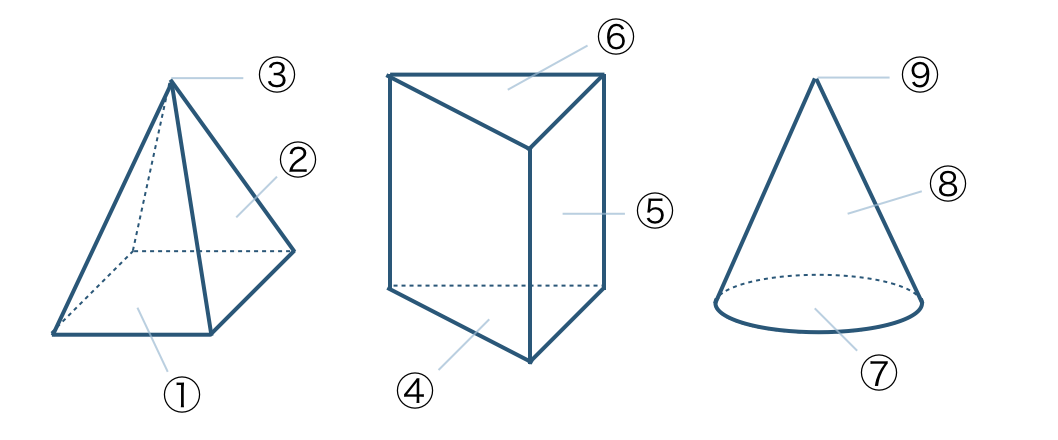
\({\small (2)}~\)次の①〜⑨の名前を答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 三角柱 ② 円柱 ③ 四角錐
④ 五角柱 ⑤ 三角錐 ⑥ 円錐
⑦ 球 ⑧ 四角柱
多面体であるのは、①、③、④、⑤、⑧
\({\small (2)}~\)
① 底面 ② 側面 ③ 頂点
④ 底面 ⑤ 側面 ⑥ 底面
⑦ 底面 ⑧ 側面 ⑨ 頂点

正多面体
次の問いに答えよ。
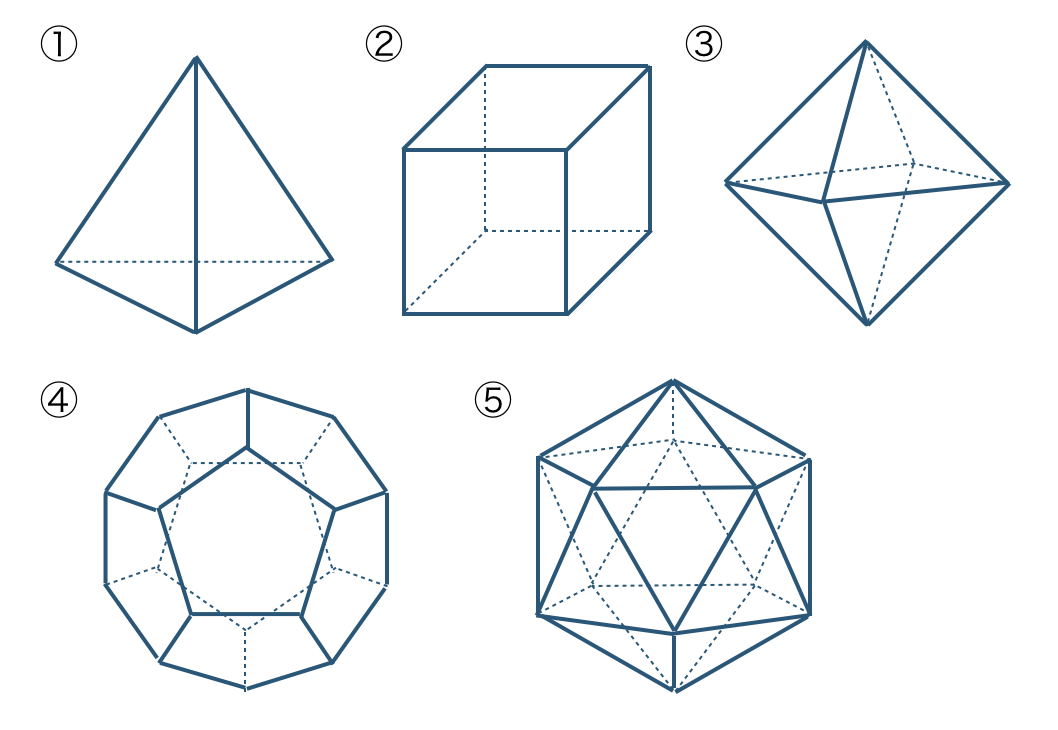
\({\small (1)}~\)次の①〜⑤の正多面体の名前を答えよ。また、面の形と1つの頂点に集まる面の数を答えよ。
\({\small (2)}~\)次の立体はすべての面が正三角形の多面体であるが、正多面体ではない。この理由を答えよ。

[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 正四面体、正三角形、\(3\) つ
② 正六面体、正方形、\(3\) つ
③ 正八面体、正三角形、\(4\) つ
④ 正十二面体、正五角形、\(3\) つ
⑤ 正二十面体、正三角形、\(5\) つ
\({\small (2)}~\)すべての面が正三角形で合同であるが、
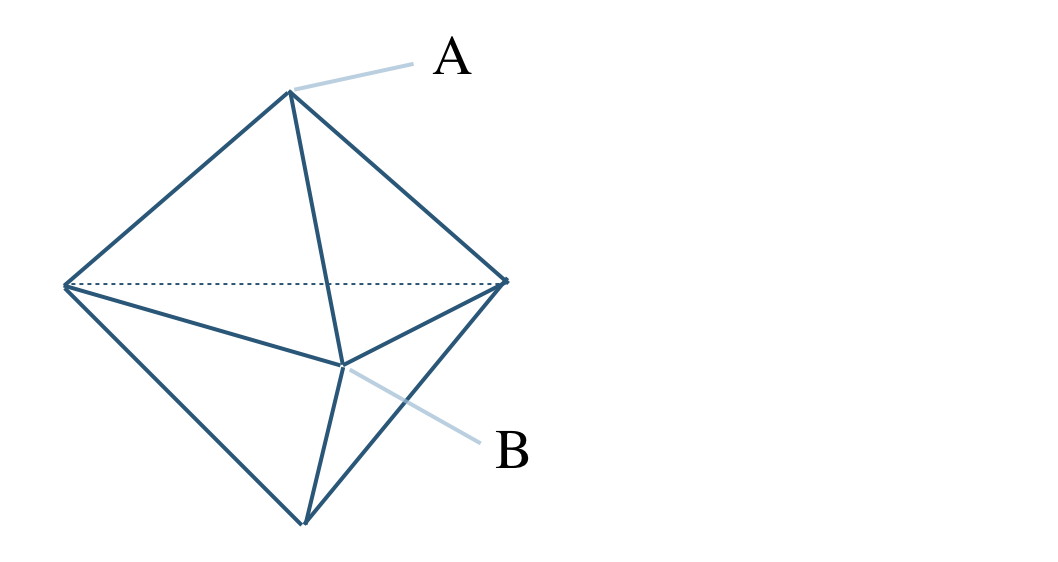
図において、
点 \({\rm A}\) に集まる面の数は \(3\) つ
点 \({\rm B}\) に集まる面の数は \(4\) つ
よって、どの頂点に集まる面の数が等しくないので、この多面体は正四面体でない

空間内の2直線
次の問いに答えよ。
\({\small (1)}~\)次の長方形について、以下の辺を答えよ。
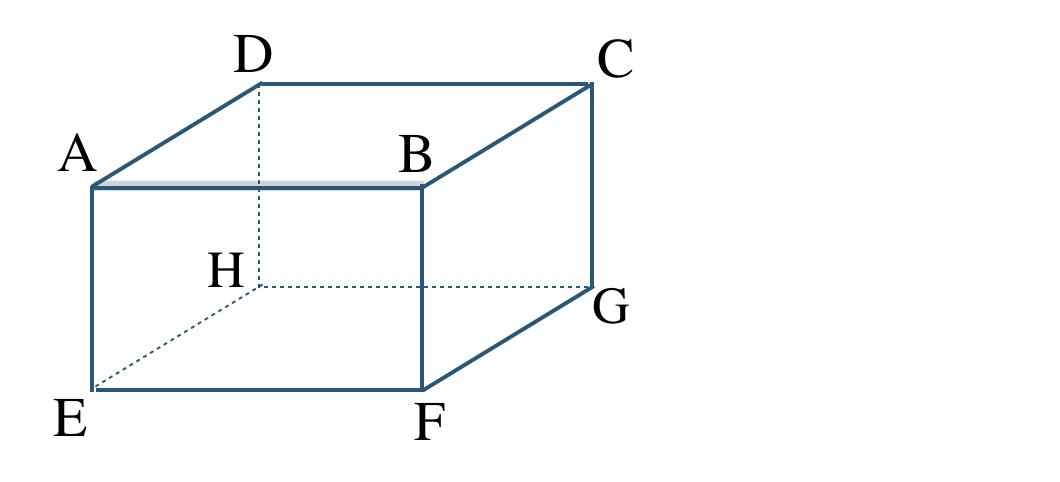
① 辺 \({\rm AB}\) と交わる辺。
② 辺 \({\rm AB}\) と平行な辺。
③ 辺 \({\rm AB}\) とねじれの位置にある辺。
\({\small (2)}~\)次の三角柱について、以下の直線を答えよ。

① 直線 \({\rm AB}\) と交わる直線。
② 直線 \({\rm AB}\) と平行な直線。
③ 直線 \({\rm AB}\) とねじれの位置にある直線。
\({\small (3)}~\)次の正四面体について、以下の直線を答えよ。
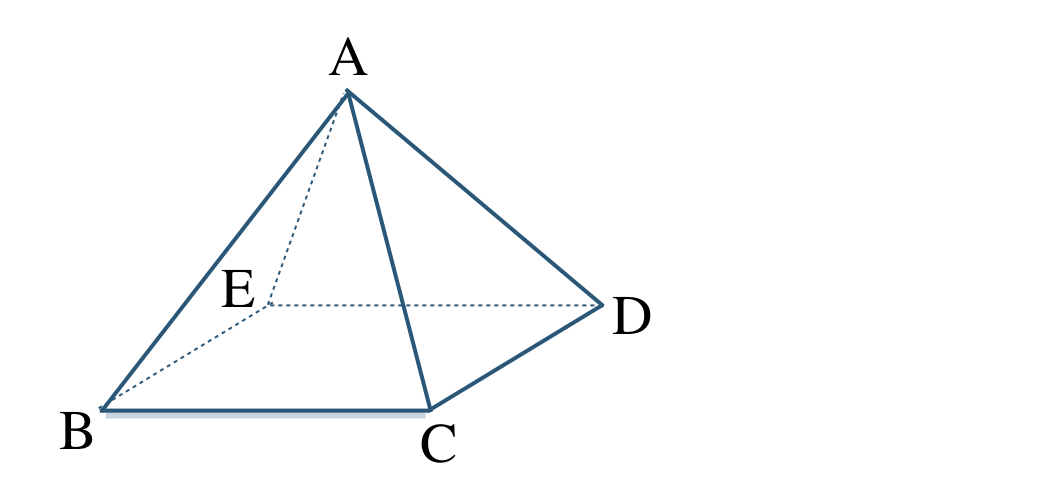
① 直線 \({\rm BC}\) と交わる直線。
② 直線 \({\rm BC}\) と平行な直線。
③ 直線 \({\rm BC}\) とねじれの位置にある直線。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 辺 \({\rm AD~,~BC~,~AE~,~BF}\)
② 辺 \({\rm DC~,~EF~,~HG}\)
③ 辺 \({\rm EH~,~FG~,~DH~,~CG}\)
\({\small (2)}~\)
① 直線 \({\rm AC~,~BC~,~AD~,~BE}\)
② 直線 \({\rm DE}\)
③ 直線 \({\rm CF~,~DF~,~EF}\)
\({\small (3)}~\)
① 直線 \({\rm AB~,~AC~,~BE~,~CD}\)
② 直線 \({\rm ED}\)
③ 直線 \({\rm AE~,~AD}\)

直線と平面の位置関係
次の問いに答えよ。
\({\small (1)}~\)次の三角柱について、以下の直線を答えよ。
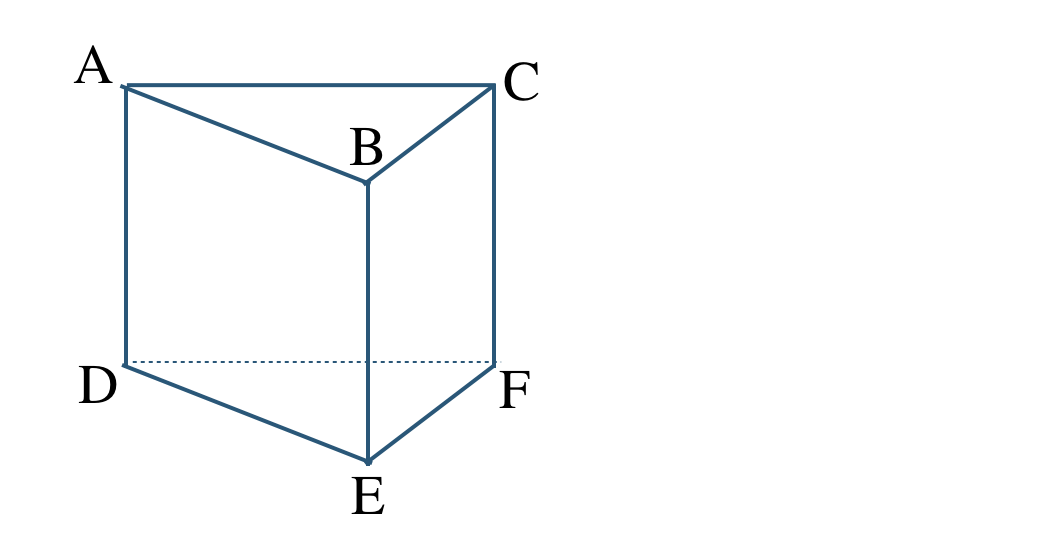
① 平面 \({\rm ABC}\) 上の直線。
② 平面 \({\rm ABC}\) と平行な直線。
③ 平面 \({\rm ABC}\) と垂直な直線。
④ 平面 \({\rm ADEB}\) と平行な直線。
\({\small (2)}~\)次の直方体の一部を切り取ってできた三角錐について、
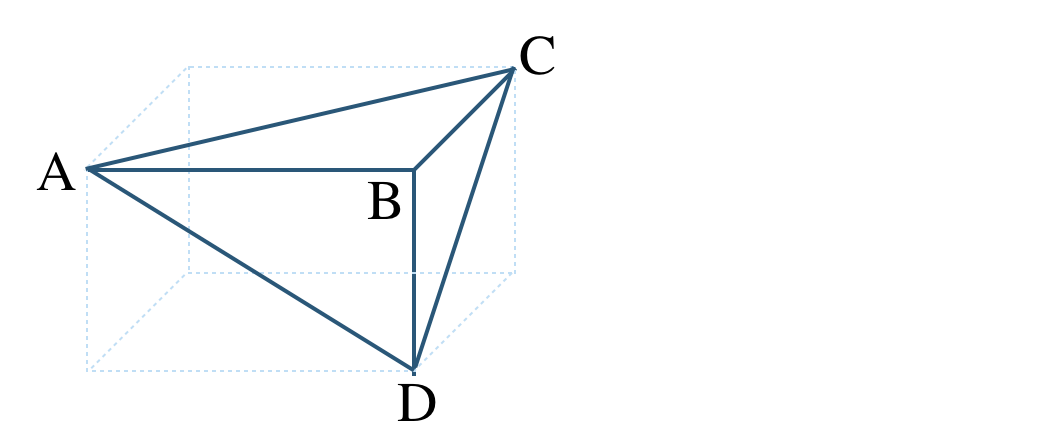
① 平面 \({\rm ABC}\) 上の直線。\(\triangle {\rm ABC}\) を底面としたときの高さを答えよ。
② 平面 \({\rm ABC}\) と平行な直線。\(\triangle {\rm BCD}\) を底面としたときの高さを答えよ。
③ \(\triangle {\rm ABD}\) を底面としたときの高さを答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 直線 \({\rm AB~,~BC~,~AC}\)
② 直線 \({\rm DE~,~EF~,~DF}\)
③ 直線 \({\rm AD~,~BE~,~CF}\)
④ 直線 \({\rm CF}\)
\({\small (2)}~\)
① 辺 \({\rm BD}\)
② 辺 \({\rm AB}\)
③ 辺 \({\rm BC}\)

2つの平面の位置関係
次の問いに答えよ。
\({\small (1)}~\)次の立方体について、以下の平面を答えよ。
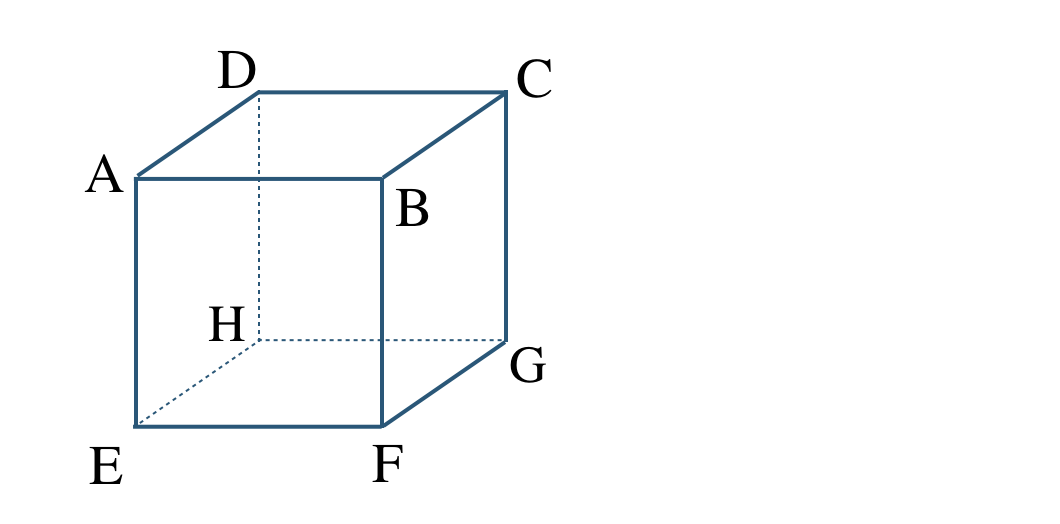
① 平面 \({\rm AEFB}\) と平行な平面
② 平面 \({\rm AEFB}\) と垂直な平面
\({\small (2)}~\)次の立方体を半分にした立体について、以下の平面を答えよ。
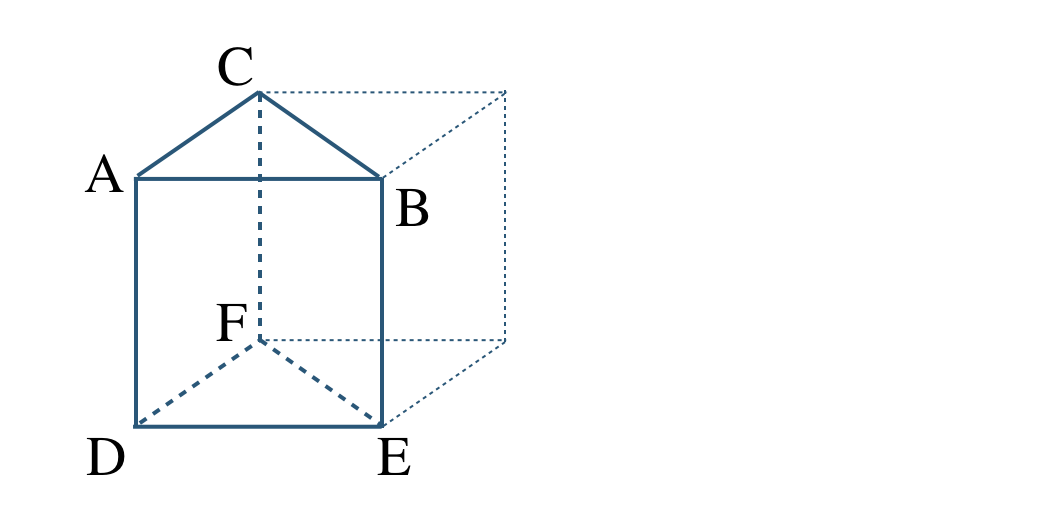
① 平面 \({\rm ABC}\) と平行な平面
② 平面 \({\rm ABC}\) と垂直な平面
③ 平面 \({\rm ADEB}\) と垂直な平面
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 平面 \({\rm DEF}\)平面 \({\rm DHGC}\)
② 平面 \({\rm ABCD~,~AEHD~,~EFGH~,~BFGC}\)
\({\small (2)}~\)
① 平面 \({\rm DEF}\)
② 平面 \({\rm ADEB~,~BEFC~,~ADFC}\)
③ 平面 \({\rm ABC~,~ADFC~,~DEF}\)

面や線が動いてできる立体
次の問いに答えよ。
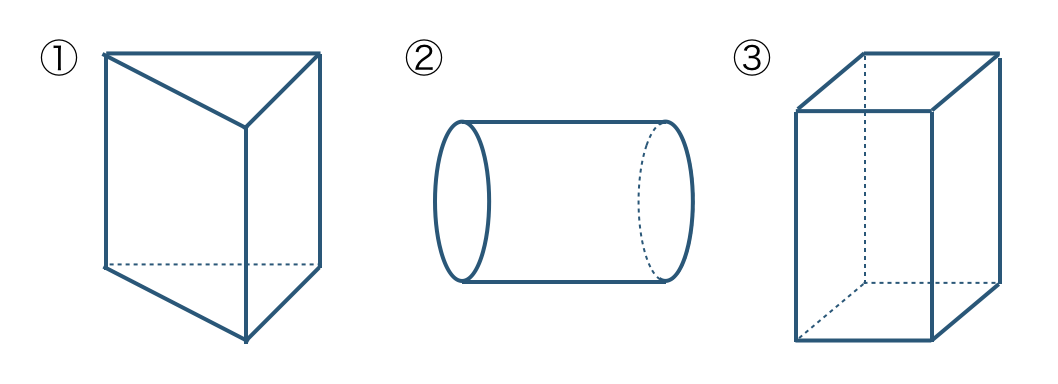
\({\small (1)}~\)次の立体は、どのような図形を動かしてできるものか答えよ。
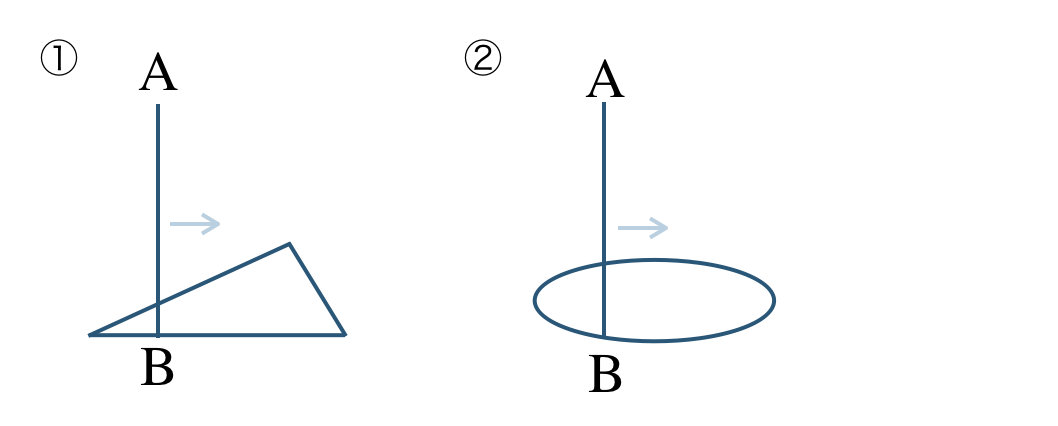
\({\small (2)}~\)次の平面上の図形の周にそって、垂直な直線 \({\rm AB}\) をひとまわり動かしてできる立体を答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 三角形を動かしてできる立体
② 円を動かしてできる立体
③ 四角形を動かしてできる立体
\({\small (2)}~\)
① 三角柱 ② 円柱

平面の回転体
次の問いに答えよ。
\({\small (1)}~\)次の図を直線 \(l\) で回転させてできる立体の見取り図をかけ。
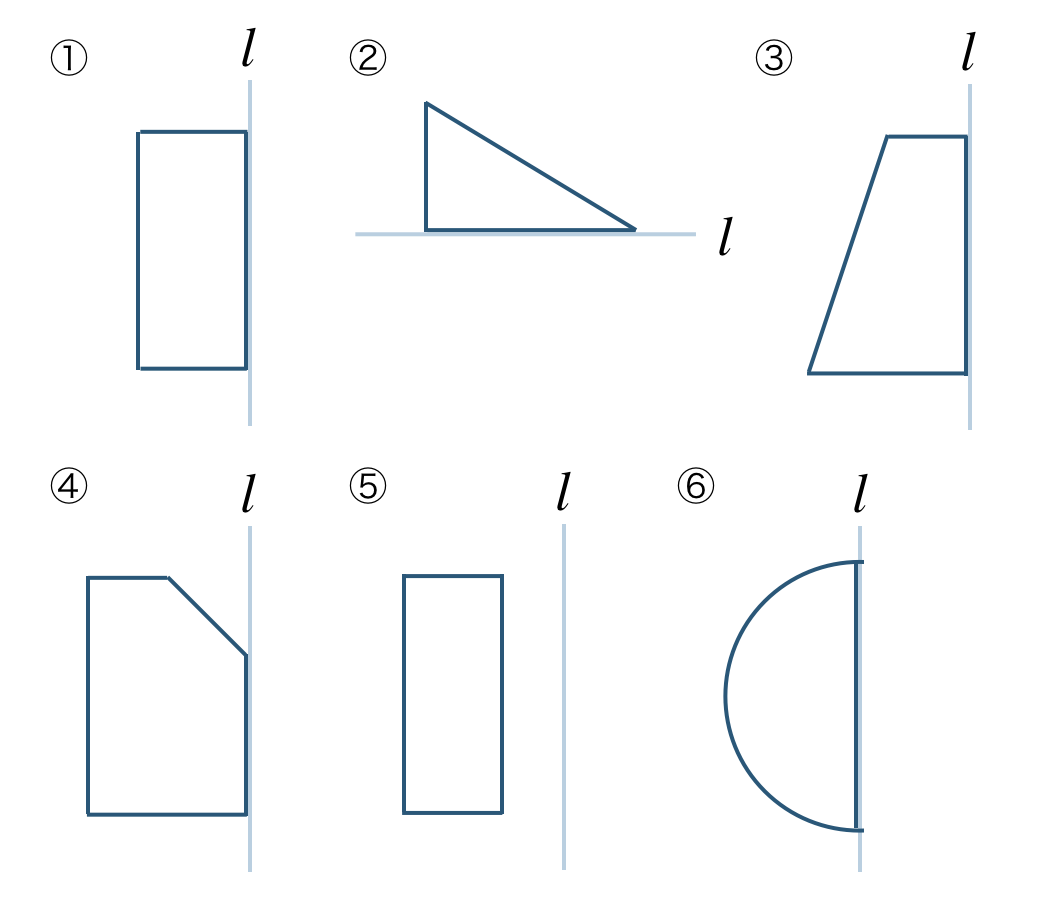
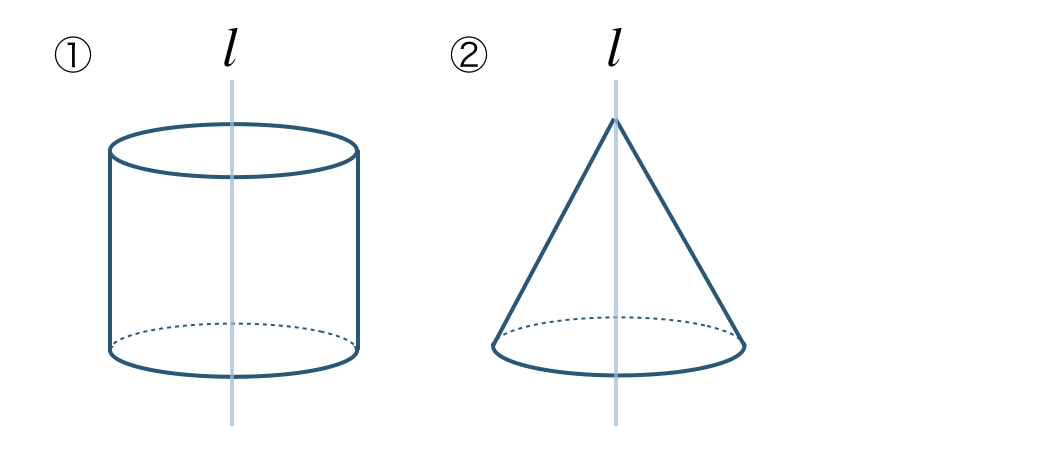
\({\small (2)}~\)次の立体を回転の軸をふくむ平面と、回転の軸に垂直な平面で切った切り口はそれぞれどな図形となるか答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
①
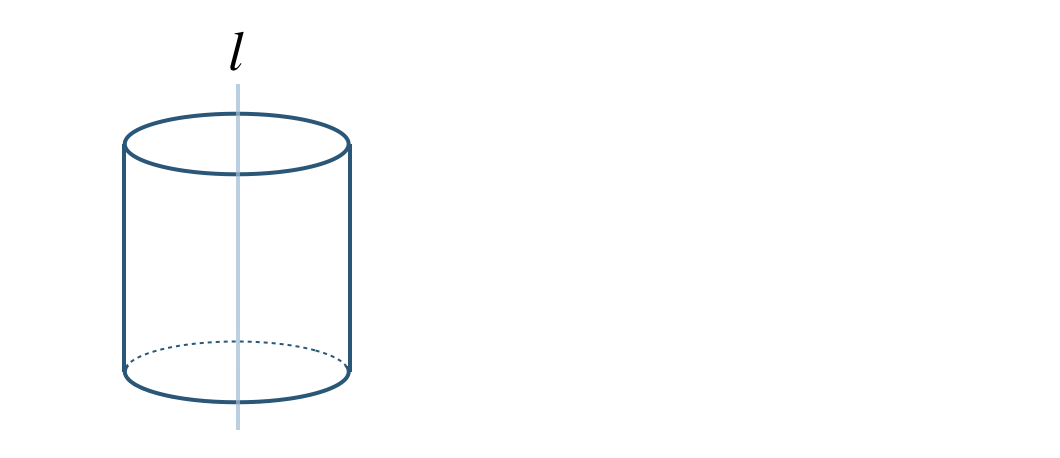
②

③
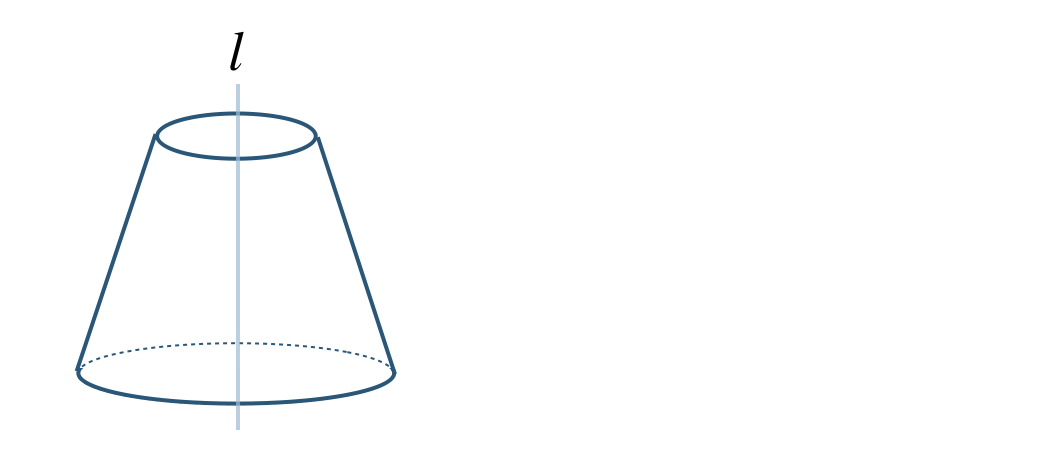
④
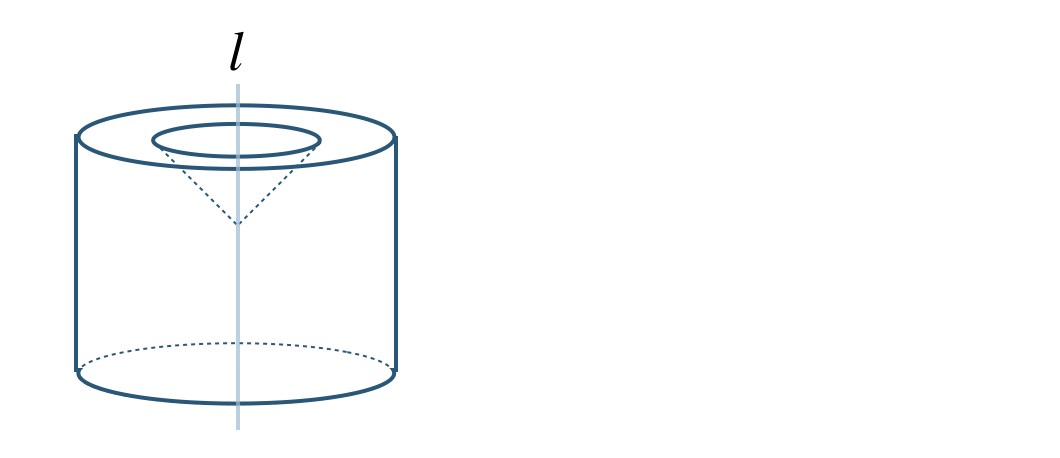
⑤
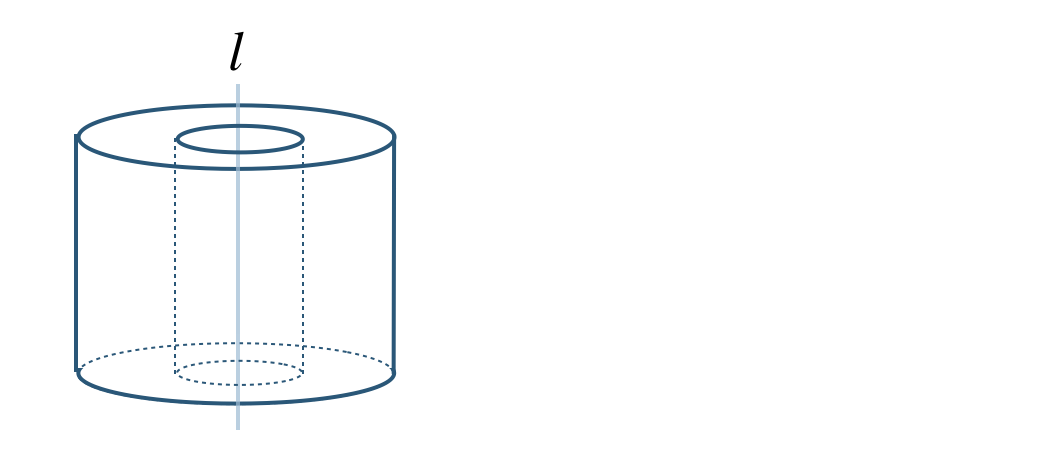
⑥

\({\small (2)}~\)
① 長方形、円
② 三角形、円

立体の展開図
次の問いに答えよ。
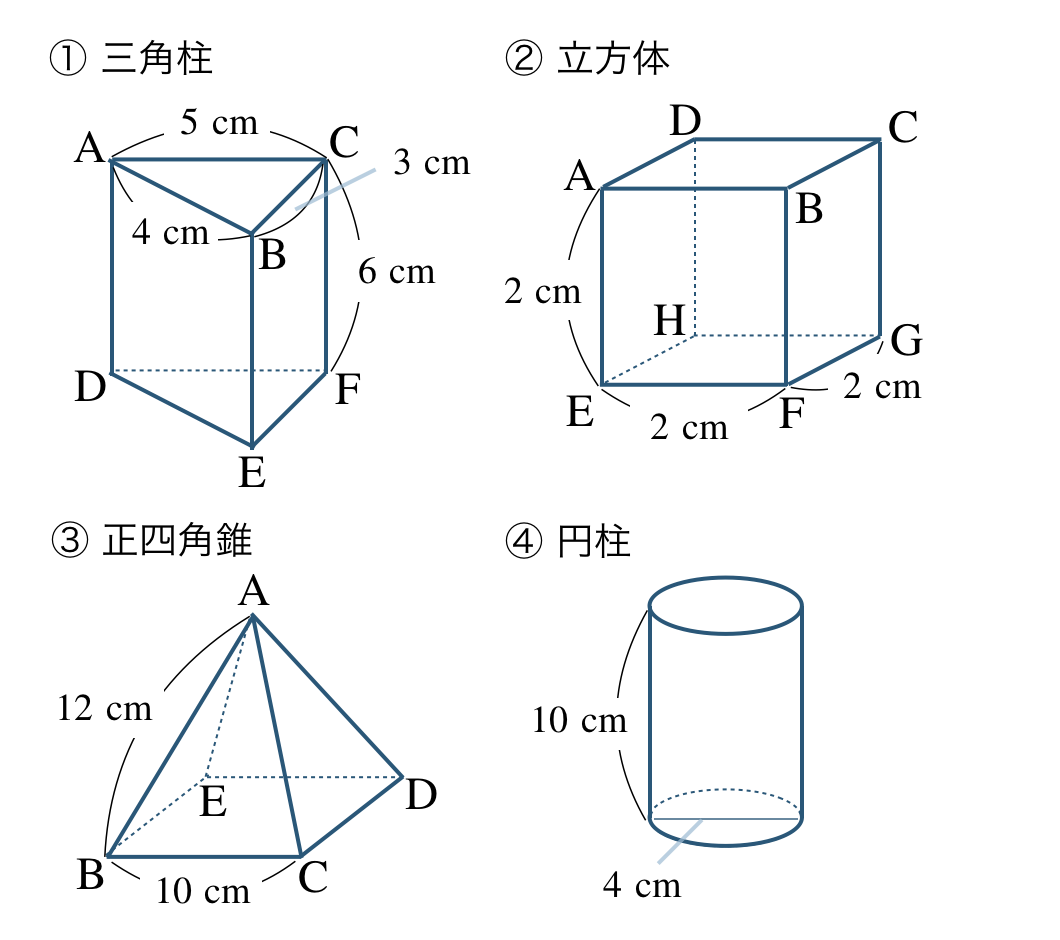
\({\small (1)}~\)次の立体の展開図をかけ。
\({\small (2)}~\)次の円錐について、

① この円錐の展開図で、側面となるおうぎ形の弧の長さと中心角を求めよ。
② この円錐の展開図をかけ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
①
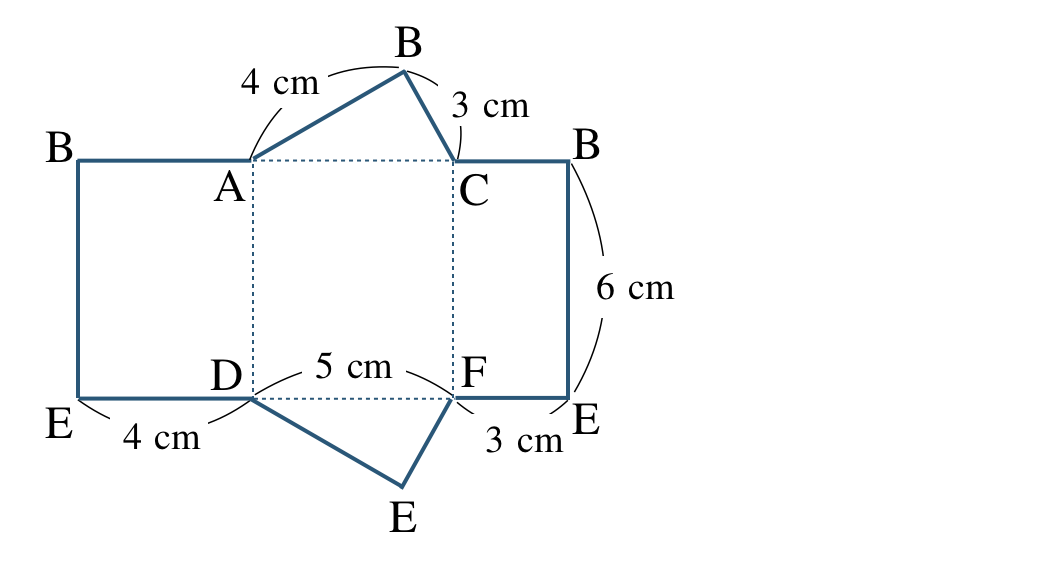
②
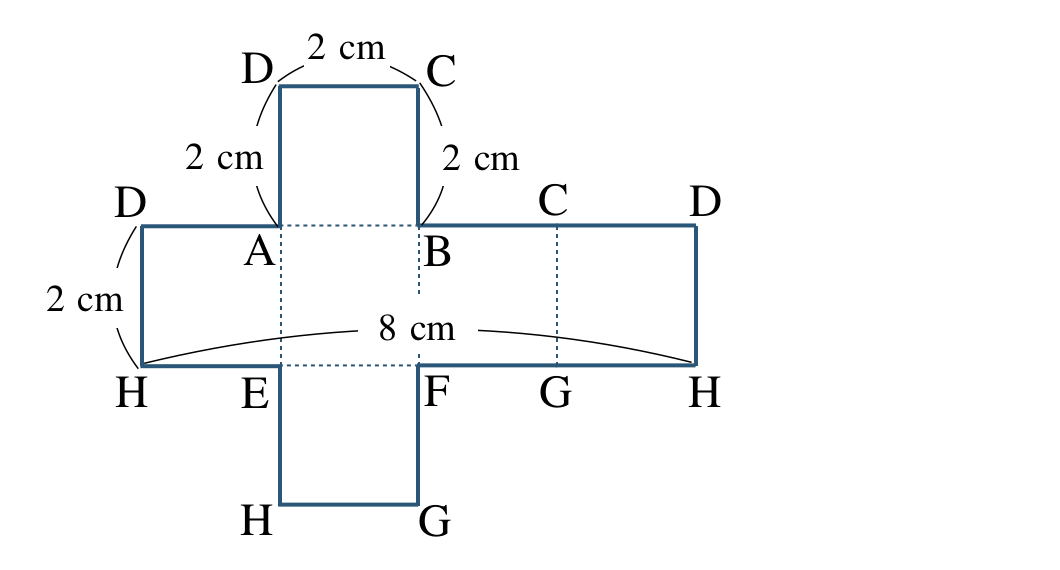
③
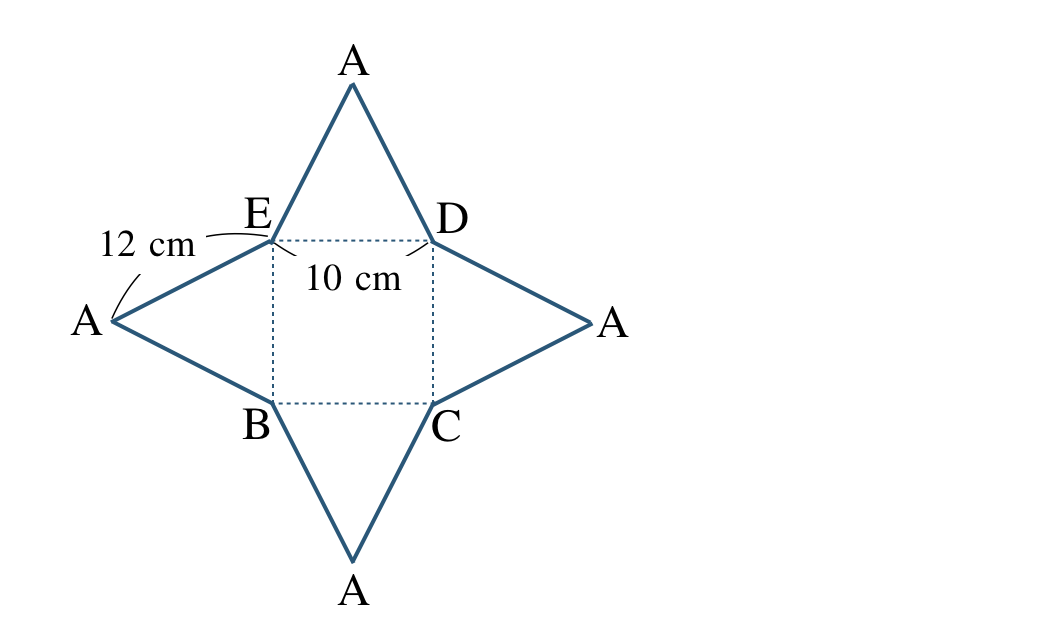
また、
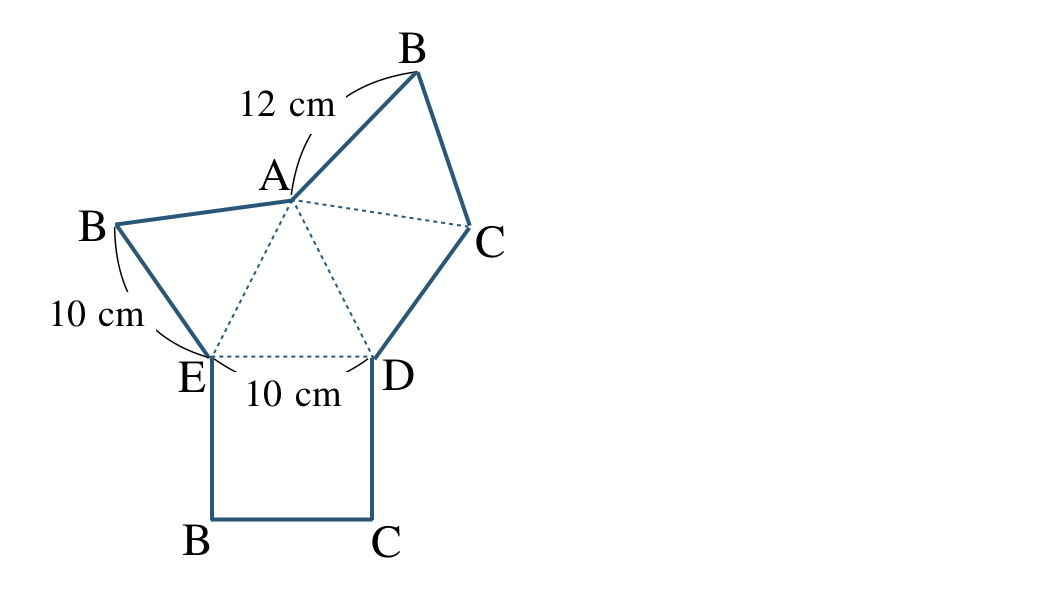
④
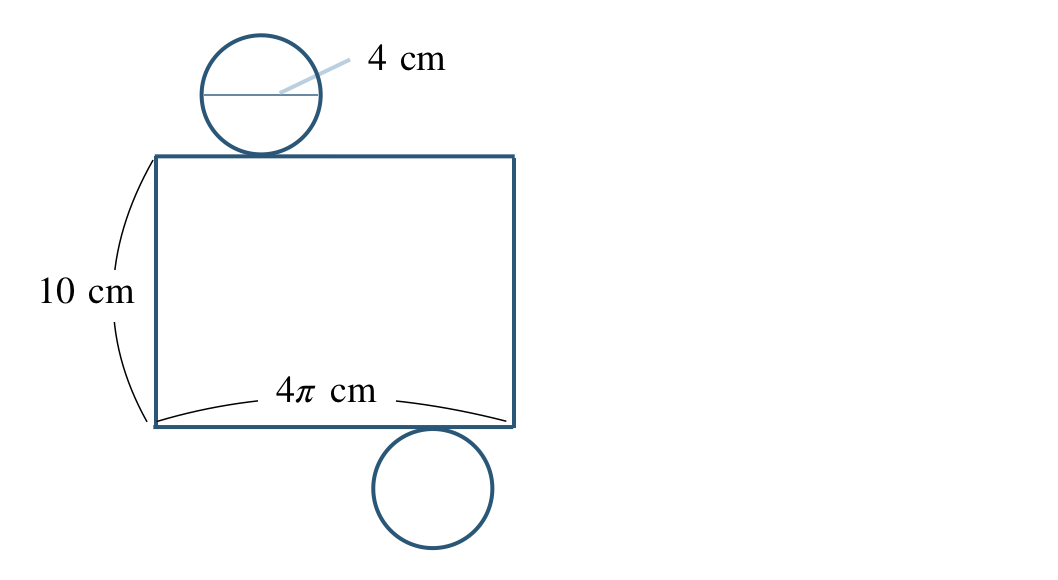
\({\small (2)}~\)
① 弧の長さ \(8\pi~{\rm cm}\)、中心角 \(120^\circ\)
②
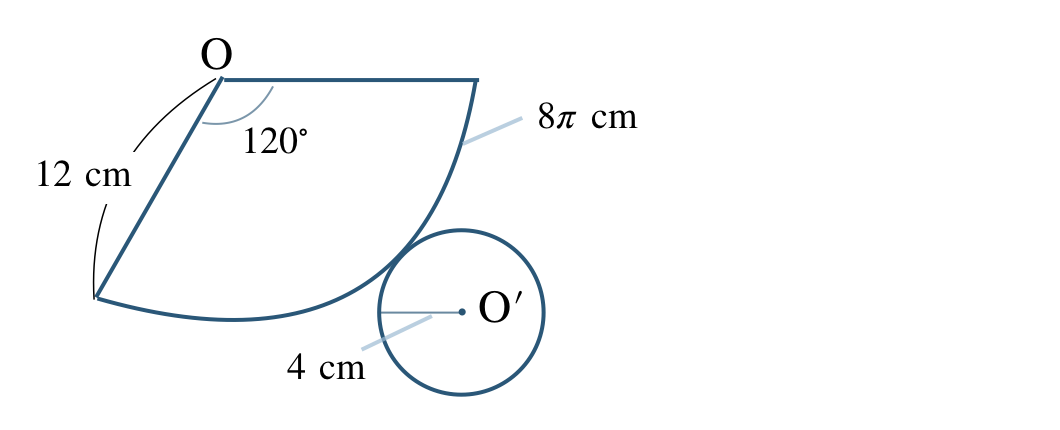

立体の投影図
次の問いに答えよ。
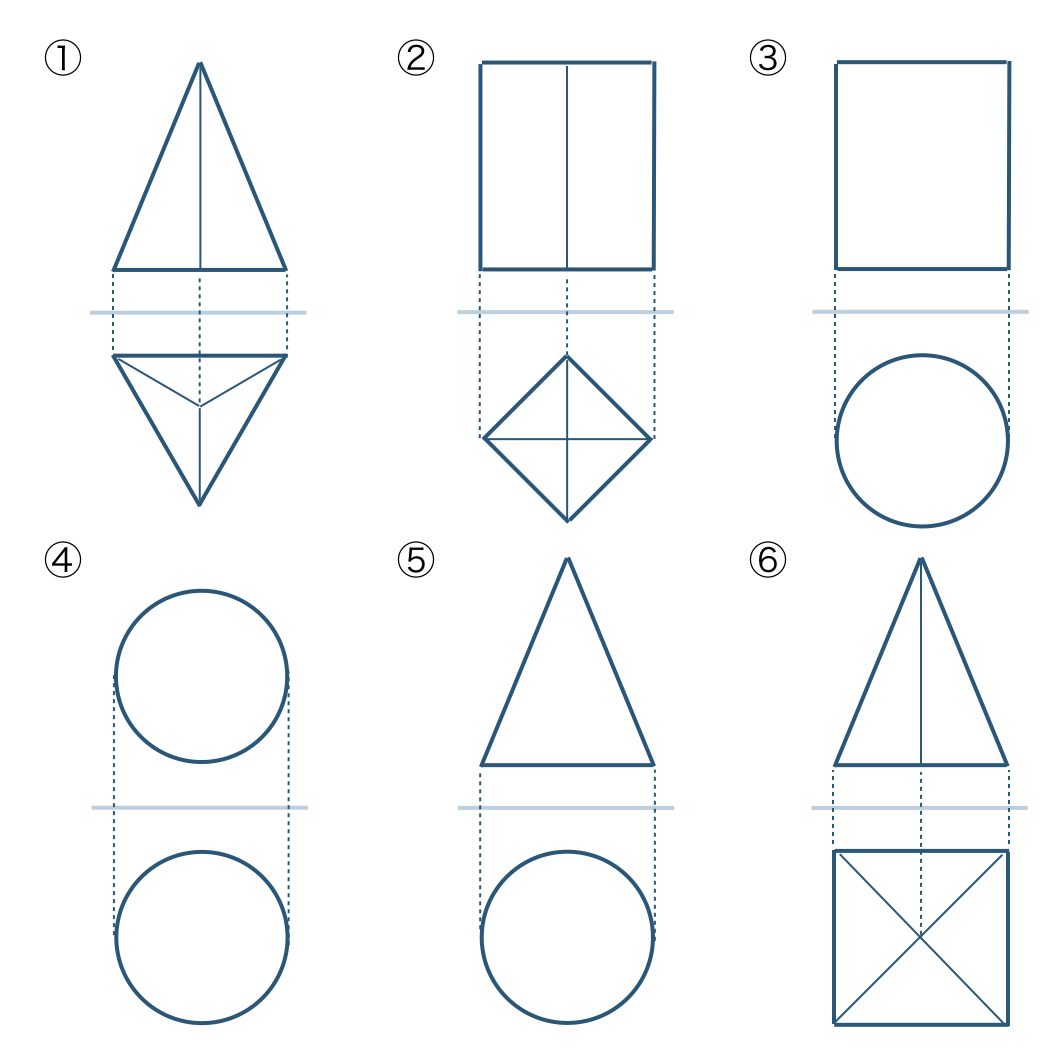
\({\small (1)}~\)次の投影図で表される立体を以下から選べ。
直方体、立方体、三角錐、四角錐
円柱、円錐、球
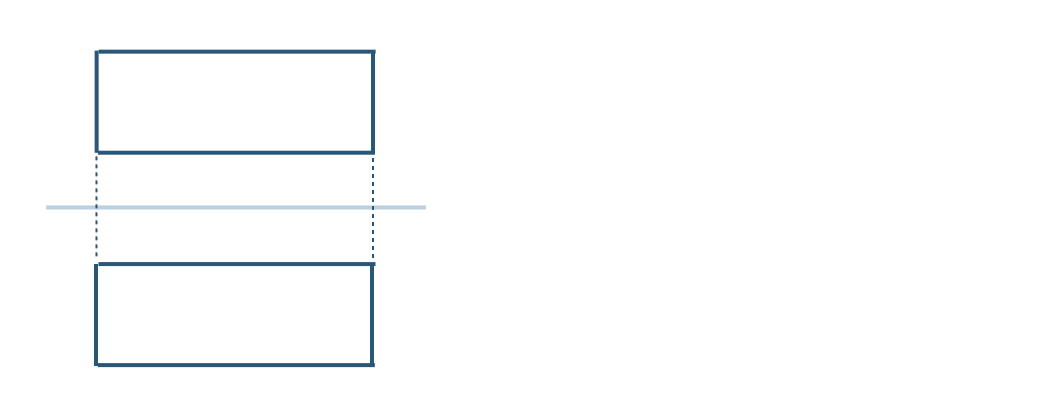
\({\small (2)}~\)次の投影図は、立面図と平面図が合同な長方形である。
この投影図は、どのような立体と考えられるか答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 三角錐 ② 直方体
③ 円柱 ④ 球
⑤ 円錐 ⑥ 四角錐
\({\small (2)}~\)
直方体(四角柱)
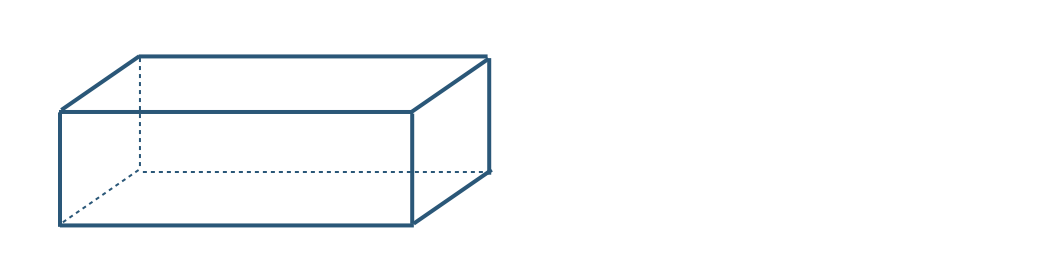
三角柱

円柱
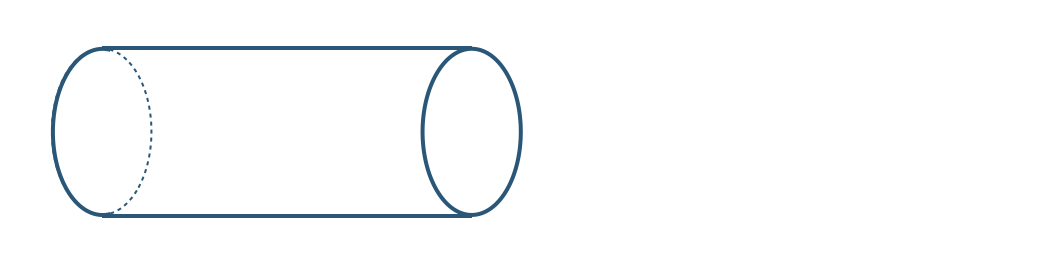
など

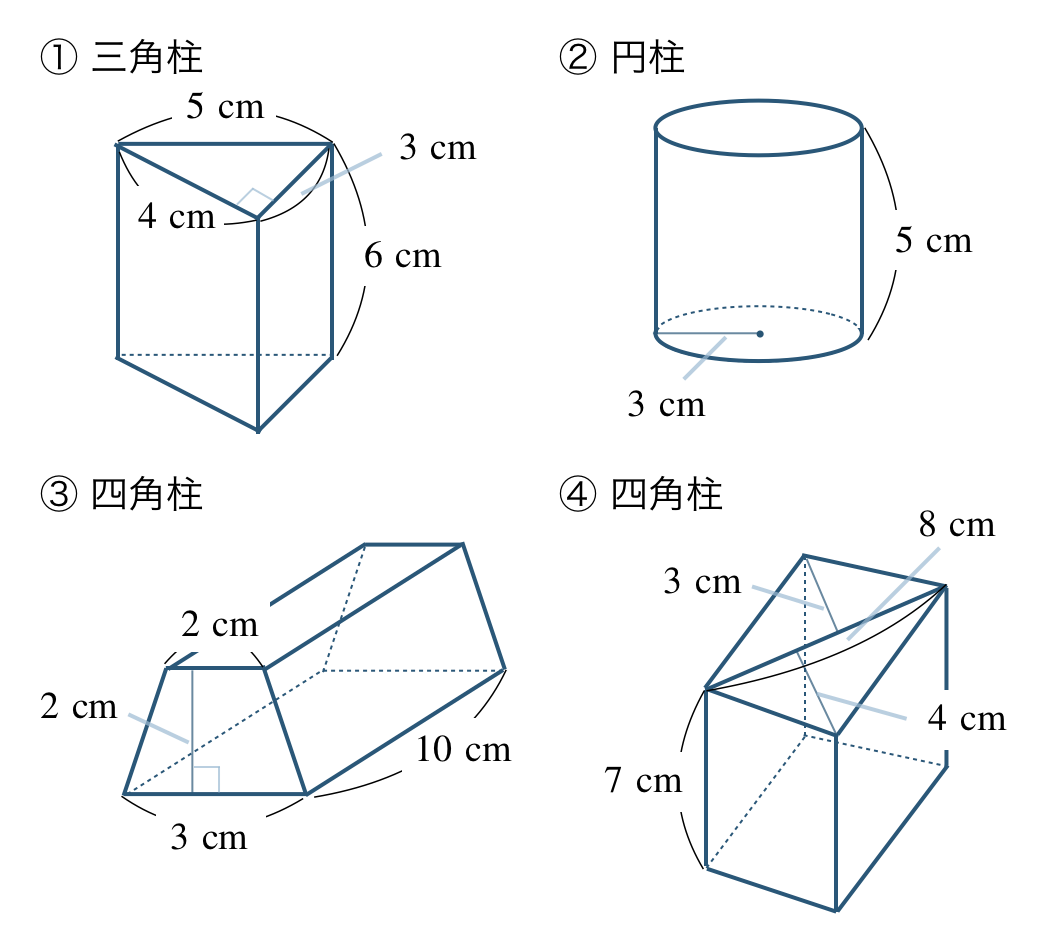
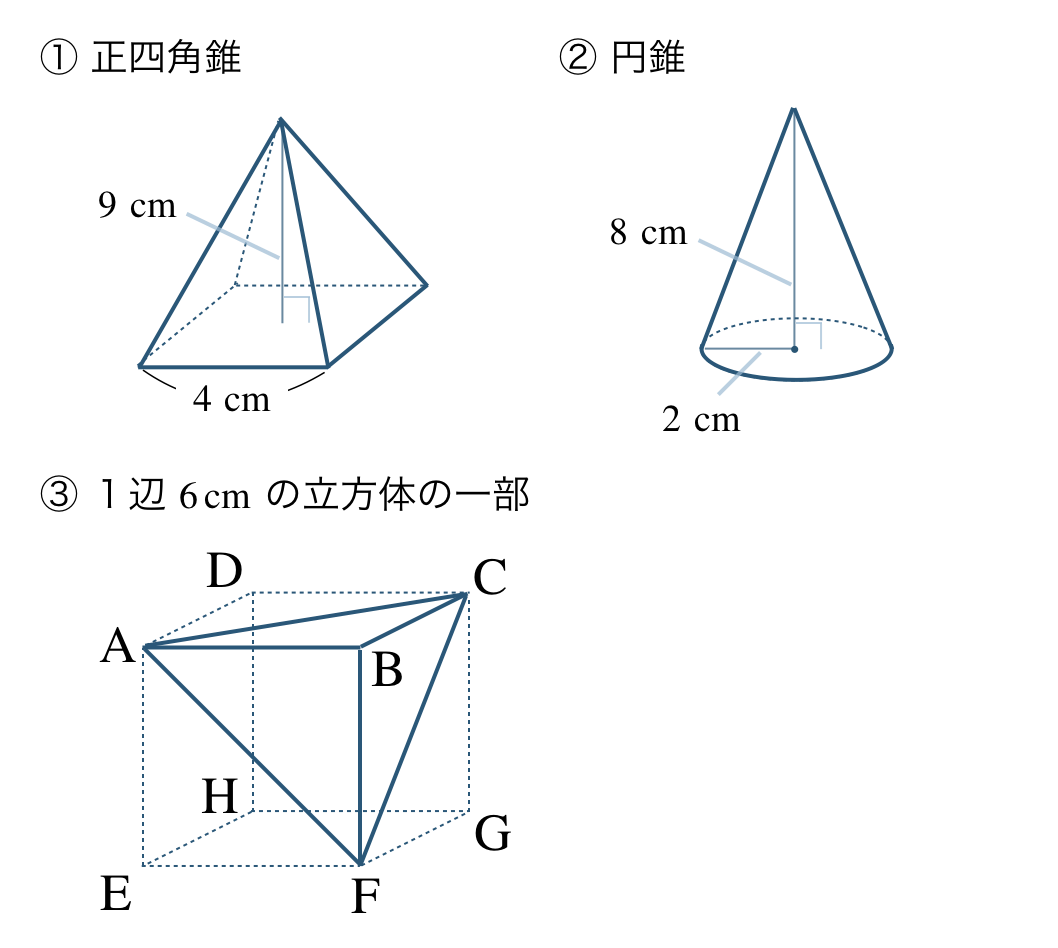
立体の体積
次の問いに答えよ。
\({\small (1)}~\)次の立体の体積を求めよ。
\({\small (2)}~\)次の立体の体積を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(36~{\rm cm}^3\)
② \(45\pi~{\rm cm}^3\)
③ \(50~{\rm cm}^3\)
④ \(196~{\rm cm}^3\)
\({\small (2)}~\)
① \(48~{\rm cm}^3\)
② \(\begin{split}{ \frac{\,32\pi\,}{\,3\,}}~{\rm cm}^3\end{split}\)
③ \(36~{\rm cm}^3\)

立体の表面積
次の問いに答えよ。
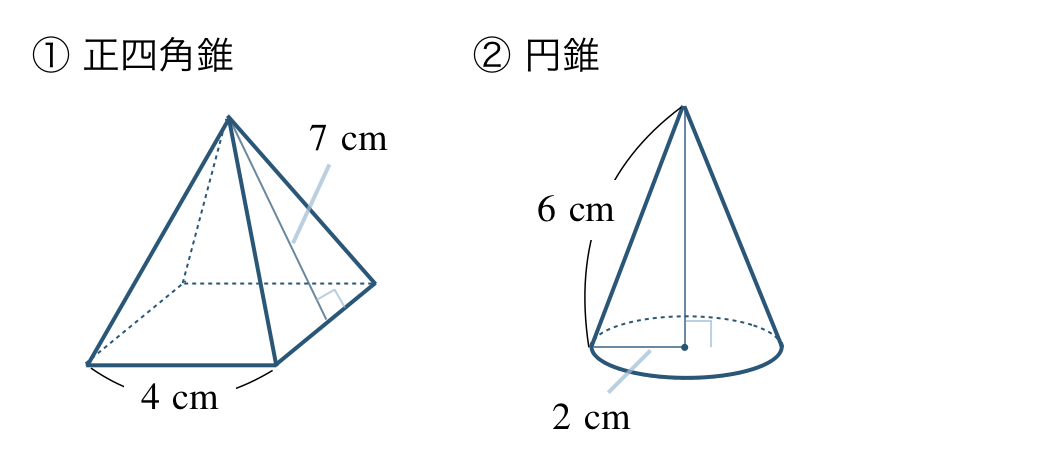
\({\small (1)}~\)次の立体の表面積を求めよ。
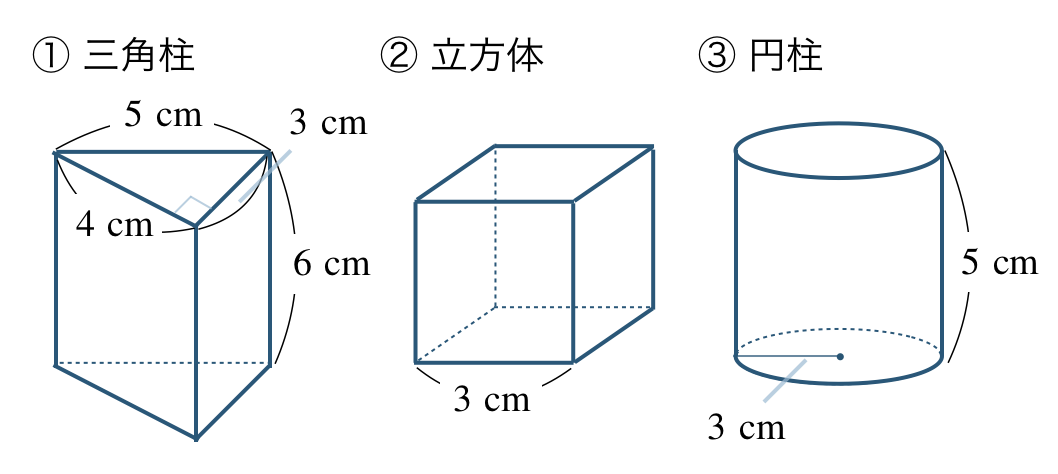
\({\small (2)}~\)次の立体の表面積を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(84~{\rm cm}^2\)
② \(54~{\rm cm}^2\)
③ \(48\pi~{\rm cm}^2\)
\({\small (2)}~\)
① \(72~{\rm cm}^2\)
② \(16\pi~{\rm cm}^2\)

球の体積と表面積
次の問いに答えよ。
\({\small (1)}~\)次の球の体積と表面積を求めよ。
① 半径 \(6~{\rm cm}\)
② 直径 \(10~{\rm cm}\)
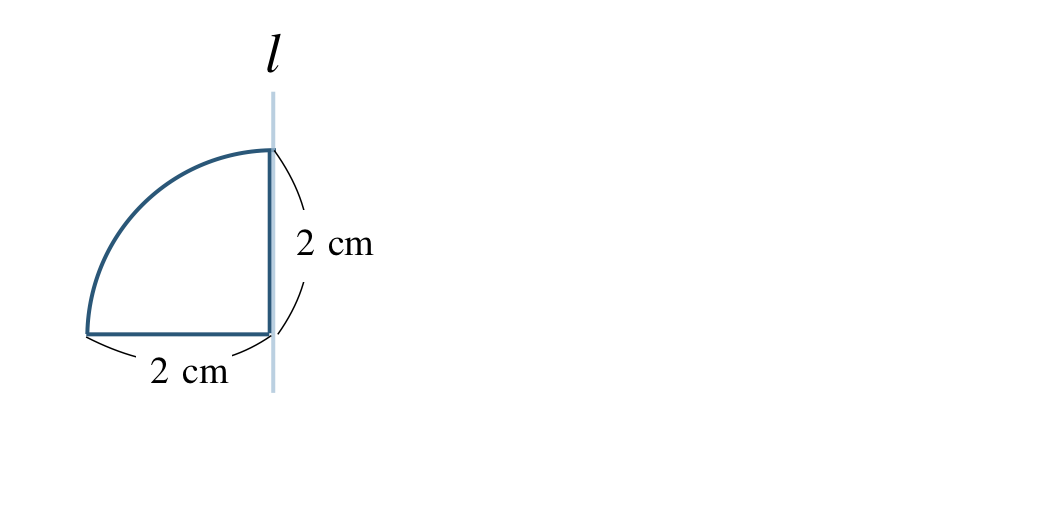
\({\small (2)}~\)次のおうぎ形を軸 \(l\) で回転させた立体の体積と表面積を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 体積 \(288~{\rm cm}^3\)、表面積 \(144~{\rm cm}^2\)
② 体積 \(\begin{split}{\frac{\,500\,}{\,3\,}}\pi~{\rm cm}^3\end{split}\)、表面積 \(100\pi~{\rm cm}^2\)
\({\small (2)}~\)
体積 \(\begin{split}{\frac{\,16\,}{\,3\,}}\pi~{\rm cm}^3\end{split}\)、表面積 \(12\pi~{\rm cm}^2\)



