今回の問題は「2つの平面の位置関係」です。
\(~\)数研出版 これからの数学1 p.196 問5~6
\(~\)東京書籍 新しい数学1 p.198~199 問5~6
\(~\)啓林館 未来へひろがる数学1 p.194 問5
問題
\({\small (1)}~\)次の立方体について、以下の平面を答えよ。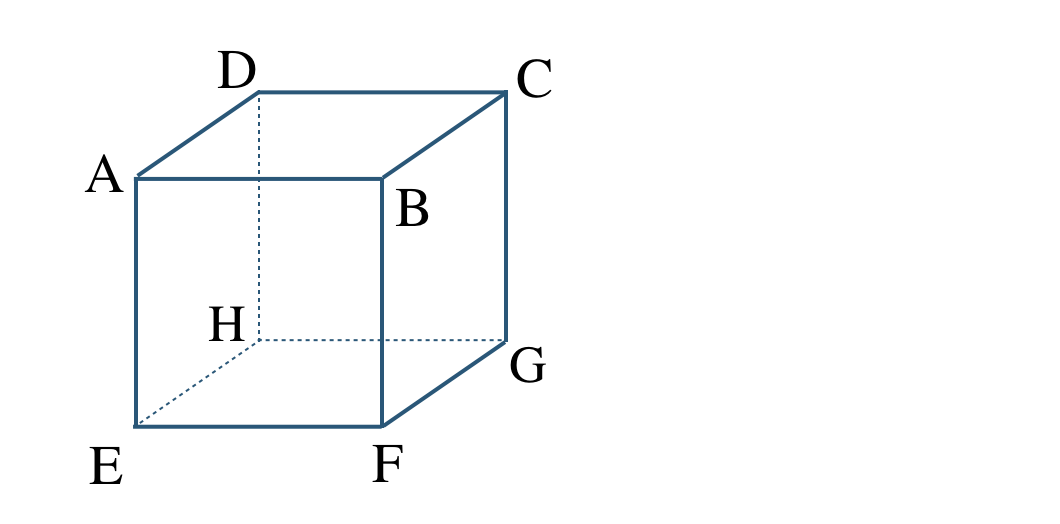
\({\small (2)}~\)次の立方体を半分にした立体について、以下の平面を答えよ。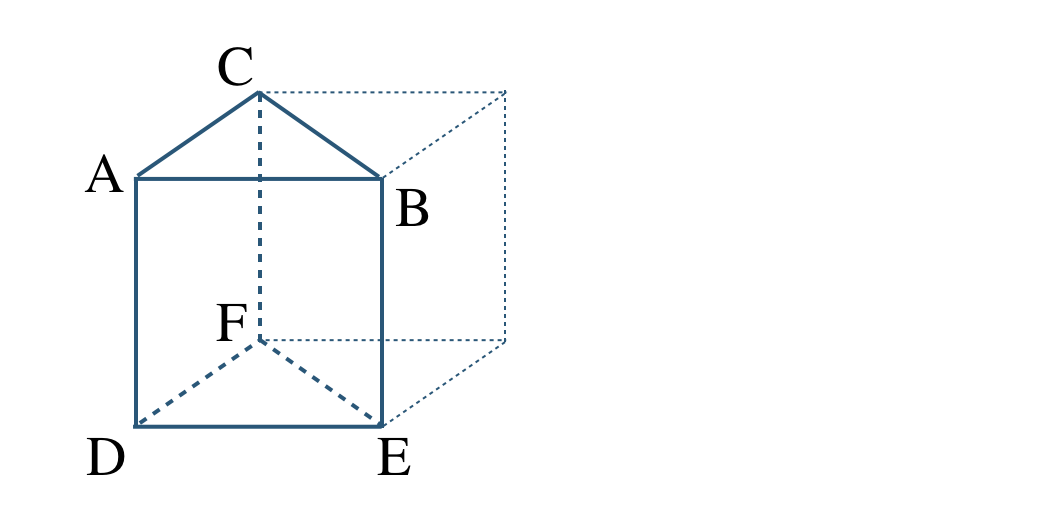
次の問いに答えよ。
\({\small (1)}~\)次の立方体について、以下の平面を答えよ。

① 平面 \({\rm AEFB}\) と平行な平面
② 平面 \({\rm AEFB}\) と垂直な平面
\({\small (2)}~\)次の立方体を半分にした立体について、以下の平面を答えよ。

① 平面 \({\rm ABC}\) と平行な平面
② 平面 \({\rm ABC}\) と垂直な平面
③ 平面 \({\rm ADEB}\) と垂直な平面
Point:2つの平面の位置関係
② 2つの平面が交わる
※ 交わる直線 \(l\) を「交線」という。
また、交線上の点から、それぞれの平面上にひいた2つの垂線がつくる角を、平面 \(\rm P~,~Q\) の「なす角」という。
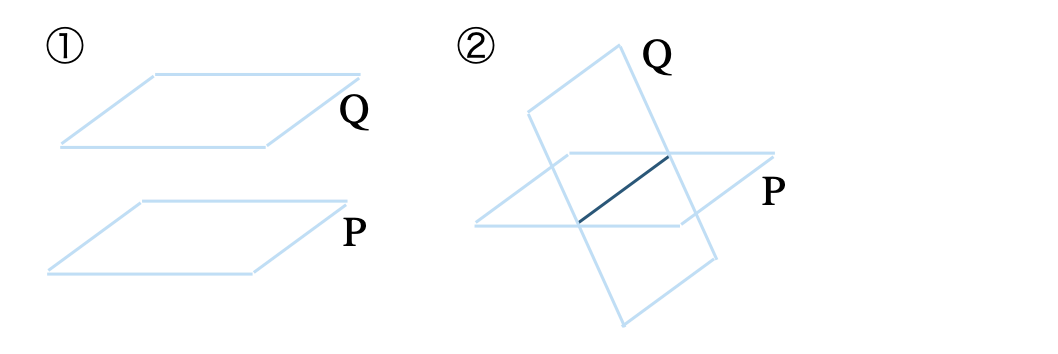
空間内の2つの平面の位置関係は、

① 2つの平面が平行である
※ 平面 \(\rm P~,~Q\) は交わらない。
② 2つの平面が交わる
※ 交わる直線 \(l\) を「交線」という。
また、交線上の点から、それぞれの平面上にひいた2つの垂線がつくる角を、平面 \(\rm P~,~Q\) の「なす角」という。

このなす角が \(90^\circ\) (直角)のとき、平面 \(\rm P~,~Q\) は垂直であるといい、\(\rm P\perp Q\) と表す。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
次のページ「解法のPointと問題解説」


