このページは「中学数学3 円の性質」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学3 円の性質
円周角の定理
次の問いに答えよ。
\({\small (1)}~\)次の角の大きさを求めよ。
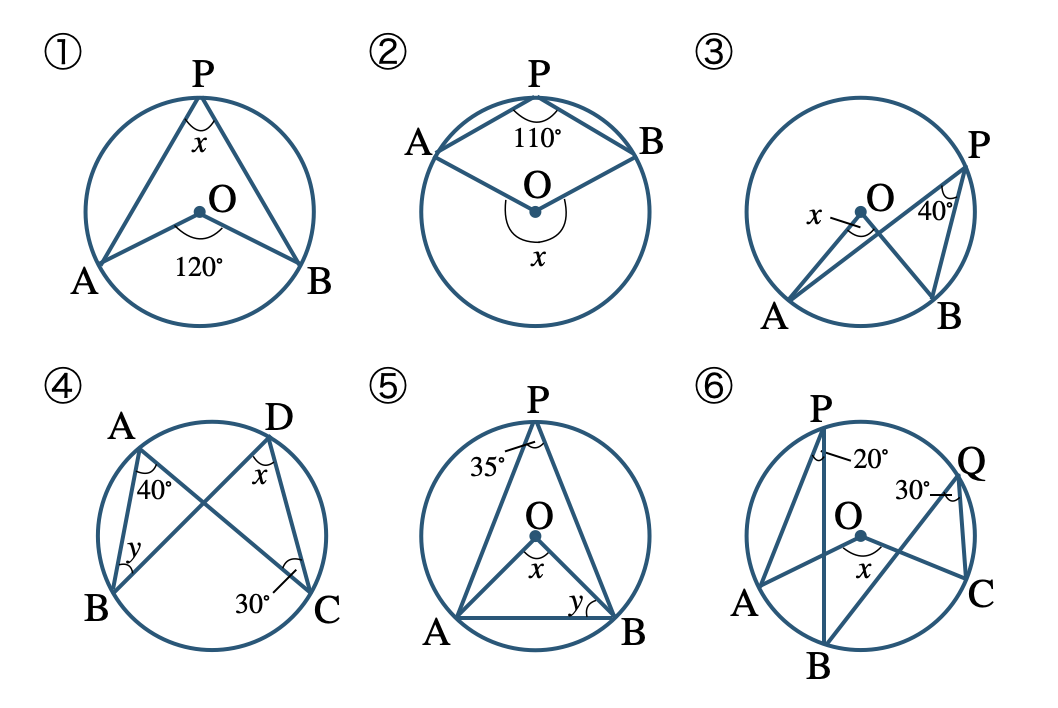
\({\small (2)}~\)次の角の大きさを求めよ。

[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(x=60^\circ\) ② \(x=220^\circ\)
③ \(x=80^\circ\) ④ \(x=40^\circ~,~y=35^\circ\)
⑤ \(x=70^\circ~,~y=55^\circ\) ⑥ \(x=100^\circ\)
\({\small (2)}~\)
① \(x=90^\circ~,~y=60^\circ\)
② \(x=40^\circ~,~y=50^\circ\)

弧の長さと円周角
次の問いに答えよ。
\({\small (1)}~\)次の角の大きさを求めよ。
① \(\overset{\frown}{{\rm AB}}=\overset{\frown}{{\rm BC}}=\overset{\frown}{{\rm CD}}\)
② \(\overset{\frown}{{\rm BC}}=2\overset{\frown}{{\rm AB}}\)

\({\small (2)}~\)次の図で、\(\overset{\frown}{{\rm AB}}=\overset{\frown}{{\rm CD}}\) ならば \({\rm AB=CD}\) であることを証明せよ。

[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(x=30^\circ~,~y=60^\circ\)
② \(x=50^\circ\)
\({\small (2)}~\)
[証明] \(\triangle {\rm OAB}\) と \(\triangle {\rm OCD}\) において、
\(\overset{\frown}{{\rm AB}}=\overset{\frown}{{\rm CD}}\) より、長さの等しい弧に対する円周角は等しいので、
\(\angle{\rm APB}=\angle{\rm CQD}~~~\cdots{\large ①}\)
円周角の定理より、
\(\angle{\rm AOB}=2\angle{\rm APB}\)
\(\angle{\rm COD}=2\angle{\rm CQD}\)
①より、
\(\angle{\rm AOB}=\angle{\rm COD}~~~\cdots{\large ②}\)
また、円の半径より、
\({\rm OA=OB}~~~\cdots{\large ③}\)
\({\rm OC=OD}~~~\cdots{\large ④}\)
②、③、④より、2組の辺とその間の角がそれぞれ等しいので、
\(\triangle {\rm OAB}\equiv\triangle {\rm OCD}\)
合同な図形では対応する辺の長さが等しいので、
\({\rm AB=CD}\)
[終]

円周角の定理の逆
次の問いに答えよ。
\({\small (1)}~\)次の①〜④の中で、4点 \({\rm A~,~B~,~C~,~D}\) が1つの円周上にあるものを選べ。

\({\small (2)}~\)次の図で、角の大きさを求めよ。

\({\small (3)}~\)次の図で、円 \({\rm O}\) の直径 \({\rm AB}\) と円上の2点 \({\rm C~,~D}\) において、直線 \({\rm AC~,~DB}\) の交点を \({\rm E}\)、直線 \({\rm AD~,~CB}\) の交点を \({\rm F}\) とするとき、4点 \({\rm C~,~D~,~E~,~F}\) は1つの円周上にあることを証明せよ。

[ 解答を見る ]
【解答】
\({\small (1)}~\)①、③、④
\({\small (2)}~\)
① \(x=30^\circ\)
② \(x=75^\circ\)
\({\small (3)}~\)
[証明] 直径 \({\rm AB}\) に対する円周角は \(90^\circ\) より、
\(\angle{\rm ACB}=\angle{\rm ADB}=90^\circ\)
これより、外角も \(90^\circ\) となるので、
\(\angle{\rm FCE}=\angle{\rm FDE}=90^\circ\)
したがって、円周角の定理の逆より、4点 \({\rm C~,~D~,~E~,~F}\) は1つの円周上にある [終]

円の接線の長さと作図
次の問いに答えよ。
\({\small (1)}~\)円 \({\rm O}\) に外部の点 \({\rm P}\) からひいた2本の接線との接点を \({\rm A~,~B}\) とするとき、\({\rm PA=PB}\) となることを証明せよ。

\({\small (2)}~\)次の図の点 \({\rm P}\) を通る円 \({\rm O}\) の接線を作図せよ。

\({\small (3)}~\)次の図で、\(x\) の長さのと \(y\) の大きさを求めよ。
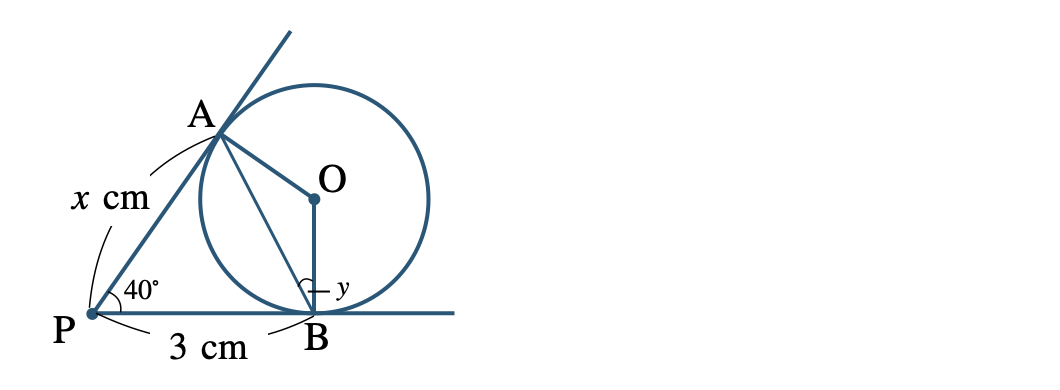
[ 解答を見る ]
【解答】
\({\small (1)}~\)
[証明] \(\triangle {\rm POA}\) と \(\triangle {\rm POB}\) について、
円の接線は接点を通る半径に垂直より、
\(\angle{\rm OAP}=\angle{\rm OBP}=90^\circ~~~\cdots{\large ①}\)
円の半径より、
\({\rm OA=OB}~~~\cdots{\large ②}\)
共通の辺より、
\({\rm PO=PO}~~~\cdots{\large ③}\)
①、②、③より、直角三角形の斜辺と他の1辺がそれぞれ等しいので、
\(\triangle {\rm POA}\equiv\triangle {\rm POB}\)
合同な図形では、対応する辺は等しいので、
\({\rm PA=PB}\)
[終]
\({\small (2)}~\)
① 線分 \({\rm PO}\) の垂直二等分線をひき、線分 \({\rm PO}\) との交点を \({\rm M}\) とする。

② 点 \({\rm M}\) を中心に半径 \({\rm MP(MO)}\) の円をかき、円 \({\rm O}\) との交点を \({\rm A~,~B}\) とする。

③ 直線 \({\rm PA~,~PB}\) が、点 \({\rm P}\) から円 \({\rm O}\) にひいた接線となる。

\({\small (3)}~\)\(x=3~{\rm cm}~,~y=20^\circ\)

円周角の定理と相似
次の証明をせよ。
\({\small (1)}~\)次の図で、弦 \({\rm AB}\) と弦 \({\rm CD}\) との交点を \({\rm P}\) とするとき、
\(\triangle {\rm PAC}\,\,\unicode{x223D}\,\,\triangle {\rm PDB}\)
であることを証明せよ。

\({\small (2)}~\)次の図で、弦 \({\rm AB}\) と弦 \({\rm CD}\) を延長した直線の交点を \({\rm P}\) とするとき、
\(\triangle {\rm PAD}\,\,\unicode{x223D}\,\,\triangle {\rm PCB}\)
であることを証明せよ。
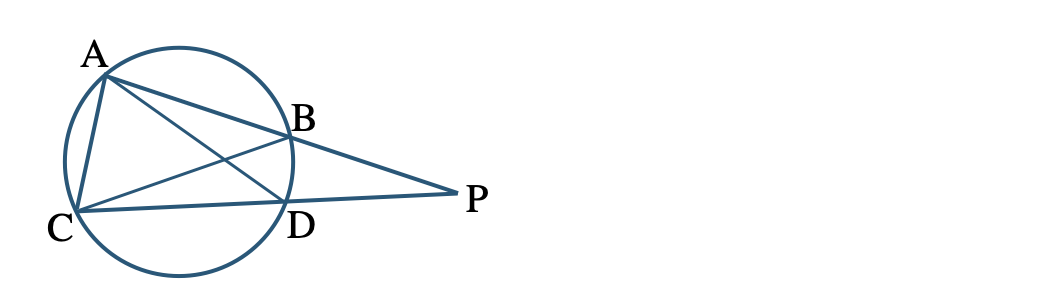
\({\small (3)}~\)次の図で、弦 \({\rm AB}\) と弦 \({\rm CD}\) との交点を \({\rm P}\) として、\(\overset{\frown}{{\rm CB}}=\overset{\frown}{{\rm BD}}\) であるとき、
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm ADP}\)
であることを証明せよ。

[ 解答を見る ]
【解答】
\({\small (1)}~\)
[証明] \(\triangle {\rm PAC}\) と \(\triangle {\rm PDB}\) について、
\(\overset{\frown}{{\rm CB}}\) に対する円周角の定理より、
\(\angle{\rm CAP}=\angle{\rm BDP}~~~\cdots{\large ①}\)
対頂角が等しいので、
\(\angle{\rm APC}=\angle{\rm DPB}~~~\cdots{\large ②}\)
①、②より、2組の角がそれぞれ等しいので、
\(\triangle {\rm PAC}\,\,\unicode{x223D}\,\,\triangle {\rm PDB}\)
[終]
\({\small (2)}~\)
[証明] \(\triangle {\rm PAD}\) と \(\triangle {\rm PCB}\) について、
\(\overset{\frown}{{\rm BD}}\) に対する円周角の定理より、
\(\angle{\rm BAD}=\angle{\rm BCD}\)
よって、
\(\angle{\rm PAD}=\angle{\rm PCB}~~~\cdots{\large ①}\)
共通の角より、
\(\angle{\rm APD}=\angle{\rm CPB}~~~\cdots{\large ②}\)
①、②より、2組の角がそれぞれ等しいので、
\(\triangle {\rm PAD}\,\,\unicode{x223D}\,\,\triangle {\rm PCB}\)
[終]
\({\small (3)}~\)
[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm ADP}\) について、
仮定 \(\overset{\frown}{{\rm CB}}=\overset{\frown}{{\rm BD}}\) より、等しい弧に対する円周角が等しいので、
\(\angle{\rm CAB}=\angle{\rm BAD}\)
よって、
\(\angle{\rm CAB}=\angle{\rm PAD}~~~\cdots{\large ①}\)
また、\(\overset{\frown}{{\rm AC}}\) に対する円周角の定理より、
\(\angle{\rm ABC}=\angle{\rm ADC}\)
よって、
\(\angle{\rm ABC}=\angle{\rm ADP}~~~\cdots{\large ②}\)
①、②より、2組の角がそれぞれ等しいので、
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm ADP}\)
[終]



