絶対値の解法
Point:絶対値
\(-3\) の絶対値は、
原点から負の方向に \(3\) 離れているので、\(3\)
また、\(0\) の絶対値は \(0\) である。
※ 正の数、負の数から符号(+や−)をとった数がその数の絶対値となる。
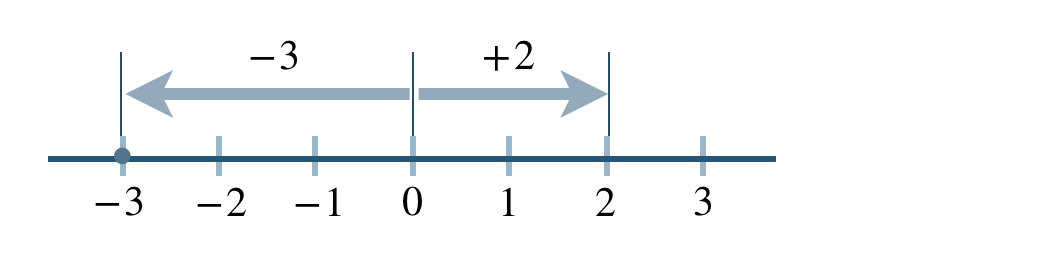
数直線上で、原点からある数までの距離を
その数の「絶対値」という。

たとえば、\(+2\) の絶対値は、
原点から正の方向に \(2\) 離れているので、\(2\)
\(-3\) の絶対値は、
原点から負の方向に \(3\) 離れているので、\(3\)
また、\(0\) の絶対値は \(0\) である。
※ 正の数、負の数から符号(+や−)をとった数がその数の絶対値となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:絶対値
問題解説(1)
問題
\({\small (1)}~\)次の数の絶対値を答えよ。
① \(+3\)
② \(-5\)
③ \(+1.5\)
④ \(\begin{split}-{ \frac{\,4\,}{\,13\,}}\end{split}\)
⑤ \(0\)
次の問いに答えよ。
\({\small (1)}~\)次の数の絶対値を答えよ。
① \(+3\)
② \(-5\)
③ \(+1.5\)
④ \(\begin{split}-{ \frac{\,4\,}{\,13\,}}\end{split}\)
⑤ \(0\)
① \(+3\)
原点から正の方向に \(3\) 離れているので、
答えは \(3\) となる
② \(-5\)
原点から負の方向に \(5\) 離れているので、
答えは \(5\) となる
③ \(+1.5\)
原点から正の方向に \(1.5\) 離れているので、
答えは \(1.5\) となる
④ \(\begin{split}-{ \frac{\,4\,}{\,13\,}}\end{split}\)
原点から負の方向に \(\begin{split}{ \frac{\,4\,}{\,13\,}}\end{split}\) 離れているので、
答えは \(\begin{split}{ \frac{\,4\,}{\,13\,}}\end{split}\) となる
⑤ \(0\)
原点からの距離が \(0\) となるので、
答えは \(0\) となる
問題解説(2)
問題
\({\small (2)}~\)絶対値が \(14\) となる数を答えよ。
次の問いに答えよ。
\({\small (2)}~\)絶対値が \(14\) となる数を答えよ。
絶対値が \(14\) より、原点からの距離が \(14\) 離れていればよいので、
正の方向に \(14\) 離れている \(+14\)
負の方向に \(14\) 離れている \(-14\)
となり、
答えは \(+14~,~-14\) となる

【問題一覧】中1|正の数と負の数
このページは「中学数学1 正の数と負の数」の問題一覧ページとなります。解説の見たい単元名がわからない...


