数の大小と不等号の解法
Point：数の大小と不等号
\({\small (1)}~\)正の数と負の数を比べるとき、
不等号＜(小なり)を使って、(負の数)\(<\)(正の数)
不等号＞(大なり)を使って、(正の数)\(>\)(負の数)
\({\small (2)}~\)正の数と正の数を比べるとき、
絶対値が大きい数が大きくなるので、
\(+1\) と \(+3\) を比べると、\(+1 < +3\)
\({\small (3)}~\)負の数と負の数を比べるとき、
絶対値が大きいほど小さい数となるので、
たとえば、\(-1\) と \(-3\) を比べると、
■ ３つの数の大小
それぞれの数の大小を比べて、
小 ＜ 中 ＜ 大 または 大 ＞ 中 ＞ 小
と表す。(※ 不等号の向きをそろえる。)
２つの数の大小を比べる方法は、
\({\small (1)}~\)正の数と負の数を比べるとき、
不等号＜(小なり)を使って、(負の数)\(<\)(正の数)
不等号＞(大なり)を使って、(正の数)\(>\)(負の数)
\({\small (2)}~\)正の数と正の数を比べるとき、
絶対値が大きい数が大きくなるので、
\(+1\) と \(+3\) を比べると、\(+1 < +3\)
\({\small (3)}~\)負の数と負の数を比べるとき、
絶対値が大きいほど小さい数となるので、
たとえば、\(-1\) と \(-3\) を比べると、
絶対値が大きい \(-3\) の方が小さい数となる
よって、\(-3<-1\) となる
■ ３つの数の大小
それぞれの数の大小を比べて、
小 ＜ 中 ＜ 大 または 大 ＞ 中 ＞ 小
と表す。(※ 不等号の向きをそろえる。)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説：数の大小と不等号
問題解説(1)
問題
\(\begin{split}{\small (1)}~-5~,~-7\end{split}\)
次の各組の数の大小を、不等号を使って表せ。
\(\begin{split}{\small (1)}~-5~,~-7\end{split}\)
数直線上で表すと、
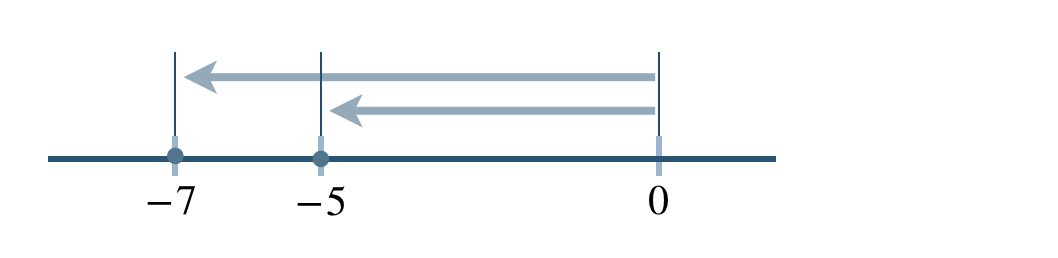
これより、
答えは、\(-7<-5\) または \(-5>-7\) となる
【別解】
それぞれの絶対値は、
\(-5\) の絶対値は \(5\)、\(-7\) の絶対値は \(7\)
絶対値は \(-7\) の方が大きい
負の数では、絶対値が大きいほど小さい数となるので、\(-7\) のほうが小さい数となる
よって、
答えは、\(-7<-5\) または \(-5>-7\) となる
問題解説(2)
問題
\(\begin{split}{\small (2)}~-3~,~+2\end{split}\)
次の各組の数の大小を、不等号を使って表せ。
\(\begin{split}{\small (2)}~-3~,~+2\end{split}\)
数直線上で表すと、
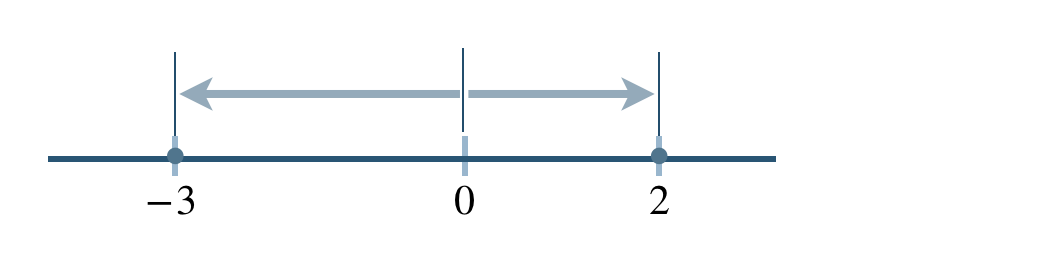
これより、答えは、
\(-3<+2\) または \(+2>-3\) となる
※ 正の数と負の数ではあきらかに正の数の方が大きい
問題解説(3)
問題
\(\begin{split}{\small (3)}~~0~,~+4~,~-6\end{split}\)
次の各組の数の大小を、不等号を使って表せ。
\(\begin{split}{\small (3)}~~0~,~+4~,~-6\end{split}\)
数直線上で表すと、
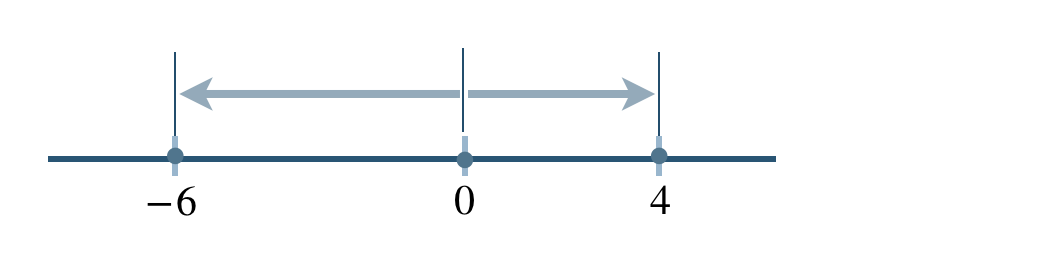
これより、答えは
\(-6<0<+4\) または \(+4>0>-6\) となる
問題解説(4)
問題
\(\begin{split}{\small (4)}~+8~,~-9~,~-10\end{split}\)
次の各組の数の大小を、不等号を使って表せ。
\(\begin{split}{\small (4)}~+8~,~-9~,~-10\end{split}\)
数直線上で表すと、
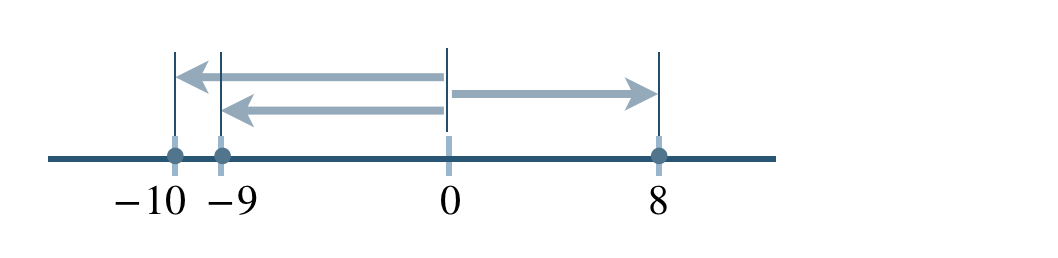
これより、答えは
\(-10<-9<+8\) または \(+8>-9>-10\) となる
問題解説(5)
問題
\(\begin{split}{\small (5)}~-1.2~,~-1.8\end{split}\)
次の各組の数の大小を、不等号を使って表せ。
\(\begin{split}{\small (5)}~-1.2~,~-1.8\end{split}\)
それぞれの絶対値は、
\(-1.2\) の絶対値は \(1.2\)、\(-1.8\) の絶対値は \(1.8\)
絶対値は \(-1.8\) の方が大きい
負の数では、絶対値が大きいほど小さい数となるので、\(-1.8\) のほうが小さい数となる
よって、
答えは、\(-1.8<-1.2\) または \(-1.2>-1.8\) となる
問題解説(6)
問題
\(\begin{split}{\small (6)}~-\frac{\,5\,}{\,7\,}~,~-\frac{\,3\,}{\,7\,}\end{split}\)
次の各組の数の大小を、不等号を使って表せ。
\(\begin{split}{\small (6)}~-\frac{\,5\,}{\,7\,}~,~-\frac{\,3\,}{\,7\,}\end{split}\)
それぞれの絶対値は、
\(\begin{split}-\frac{\,5\,}{\,7\,}\end{split}\) の絶対値は \(\begin{split}\frac{\,5\,}{\,7\,}\end{split}\)、\(\begin{split}-\frac{\,3\,}{\,7\,}\end{split}\) の絶対値は \(\begin{split}\frac{\,3\,}{\,7\,}\end{split}\)
絶対値は \(\begin{split}-\frac{\,5\,}{\,7\,}\end{split}\) の方が大きい
負の数では、絶対値が大きいほど小さい数となるので、\(\begin{split}-\frac{\,5\,}{\,7\,}\end{split}\) のほうが小さい数となる
よって、答えは
\(\begin{split}-\frac{\,5\,}{\,7\,}<-\frac{\,3\,}{\,7\,}\end{split}\) または \(\begin{split}-\frac{\,3\,}{\,7\,}>-\frac{\,5\,}{\,7\,}\end{split}\)
となる
【問題一覧】中１｜正の数と負の数
このページは「中学数学１ 正の数と負の数」の問題一覧ページとなります。解説の見たい単元名がわからない...
jhs.yorikuwa.com
