問題:正の数・負の数の加法
次の計算をせよ。
\({\small (1)}~~(+4)+(+2)\)
\({\small (2)}~~(-8)+(+3)\)
\({\small (3)}~~(+3)+(-7)\)
\({\small (4)}~~(-2)+(-3)\)
\({\small (5)}~~0+(+2)\)
\({\small (6)}~~(-5)+0\)
\({\small (7)}~~(-3)+(+3)\)
\({\small (8)}~~(-5)+(-9)\)
解法のPoint
■ 同じ符号の加法
\((-1)+(-2)\) を数直線上に表すと、
原点から負の方向に \(1\) 進んで、さらに \(2\) 進む
これより、原点から負の方向に \(3\) 進むので、
\((-1)+(-2)=-3\)
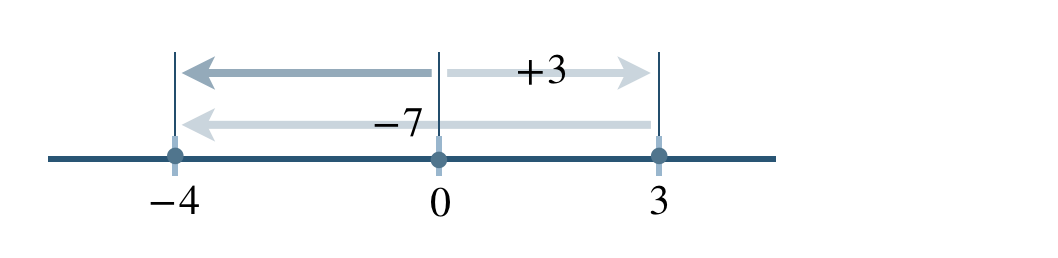
■ 異なる符号の加法
\((-2)+(+3)\) を数直線上に表すと、
原点から負の方向に \(2\) 進んで、さらにそこから正の方向に \(3\) 進む

これより、原点から正の方向に \(1\) 進むので、
\((-2)+(+3)=+1\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
■ 同じ符号の加法
符号は共通の符号で、数は絶対値の和
たとえば、\((-1)+(-2)\) では、
符号はマイナス、数は \(1+2\)
よって、
\(\begin{split}&(-1)+(-2)
\\[2pt]=~&-(1+2)
\\[2pt]=~&-3
\end{split}\)
■ 異なる符号の加法
符号は絶対値の大きい方の符号で、
数は絶対値の大きい方から小さい方の差
たとえば、\((-2)+(+3)\) では、
符号はプラス、数は \(3-2\)
よって、
\(\begin{split}&(-2)+(+3)
\\[2pt]=~&+(3-2)
\\[2pt]=~&+1
\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:正の数・負の数の加法
問題解説(1)
次の計算をせよ。
\({\small (1)}~~(+4)+(+2)\)
数直線上の移動で考えると、
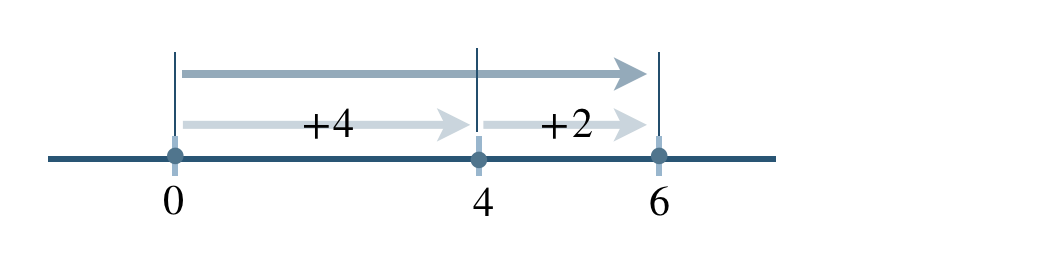
これより、
\((+4)+(+2)=+6\)
したがって、答えは \(+6\) となる
【別解】
同じ符号であるから、共通の符号で、絶対値の和より、
\(\begin{split}&(+4)+(+2)\\[2pt]~~=~&+(4+2)\\[2pt]~~=~&+6\end{split}\)
したがって、答えは \(+6\) となる
問題解説(2)
次の計算をせよ。
\({\small (2)}~~(-8)+(+3)\)
数直線上の移動で考えると、
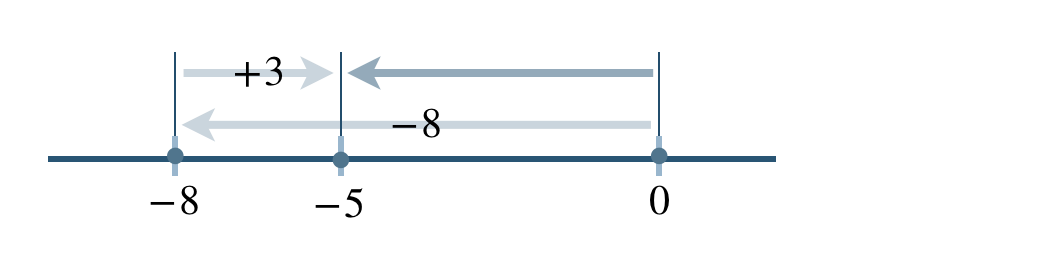
これより、
\((-8)+(+3)=-5\)
したがって、答えは \(-5\) となる
【別解】
異なる符号で絶対値は \(-8\) の方が大きいので、絶対値の大きい符号で、絶対値の大きい方から小さい方の差より、
\(\begin{split}&(-8)+(+3)\\[2pt]~~=~&-(8-3)\\[2pt]~~=~&-5\end{split}\)
したがって、答えは \(-5\) となる
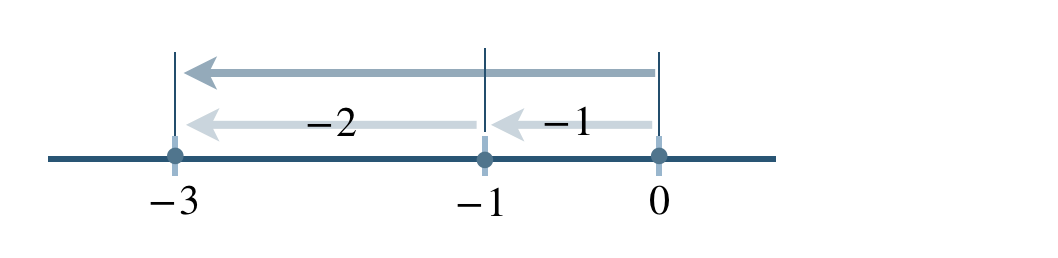
問題解説(3)
次の計算をせよ。
\({\small (3)}~~(+3)+(-7)\)
数直線上の移動で考えると、
これより、
\((+3)+(-7)=-4\)
したがって、答えは \(-4\) となる
【別解】
異なる符号で絶対値は \(-7\) の方が大きいので、絶対値の大きい符号で、絶対値の大きい方から小さい方の差より、
\(\begin{split}&(+3)+(-7)\\[2pt]~~=~&-(7-3)\\[2pt]~~=~&-4\end{split}\)
したがって、答えは \(-4\) となる
問題解説(4)
次の計算をせよ。
\({\small (4)}~~(-2)+(-3)\)
数直線上の移動で考えると、
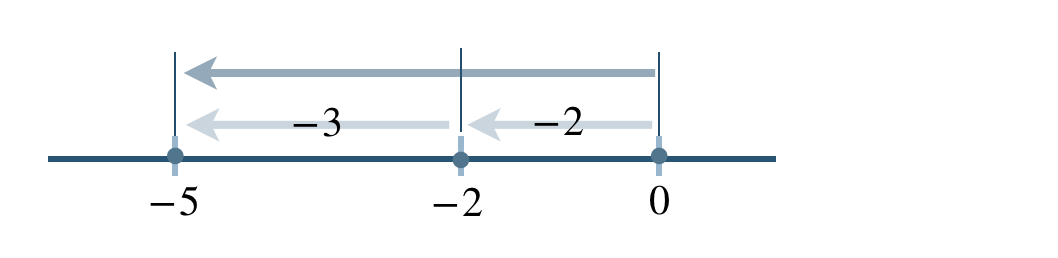
これより、
\((-2)+(-3)=-5\)
したがって、答えは \(-5\) となる
【別解】
同じ符号であるから、共通の符号で、絶対値の和より、
\(\begin{split}&(-2)+(-3)\\[2pt]~~=~&-(2+3)\\[2pt]~~=~&-5\end{split}\)
したがって、答えは \(-5\) となる
問題解説(5)
次の計算をせよ。
\({\small (5)}~~0+(+2)\)
数直線上の移動で考えると、
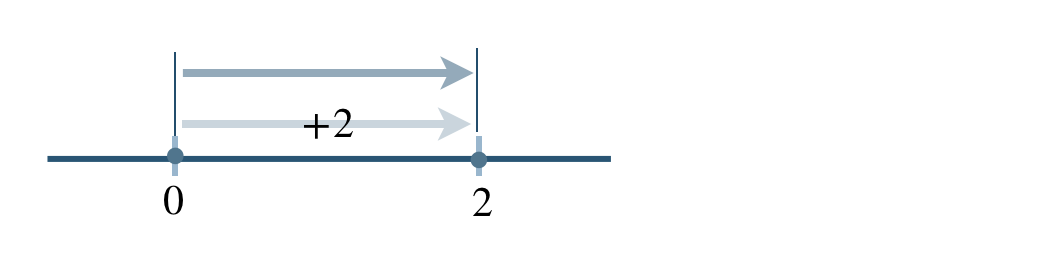
これより、
\(0+(+2)=+2\)
したがって、答えは \(+2\) となる
※ \(0\) にある数を加えると、加えた数がそのまま答えとなる。
問題解説(6)
次の計算をせよ。
\({\small (6)}~~(-5)+0\)
数直線上の移動で考えると、
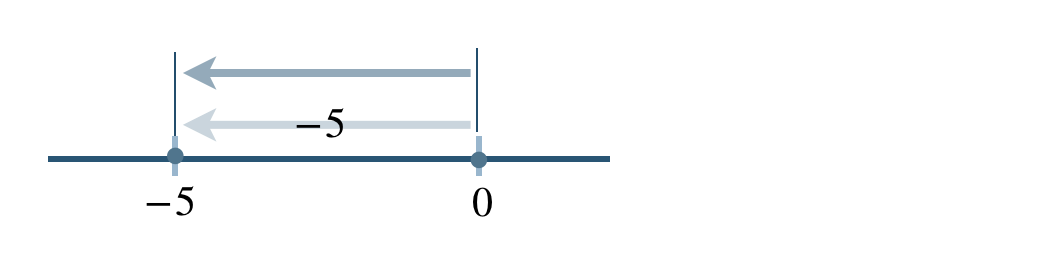
これより、
\((-5)+0=-5\)
したがって、答えは \(-5\) となる
※ \(0\) を加えても、元の数とかわらない。
問題解説(7)
次の計算をせよ。
\({\small (7)}~~(-3)+(+3)\)
数直線上の移動で考えると、
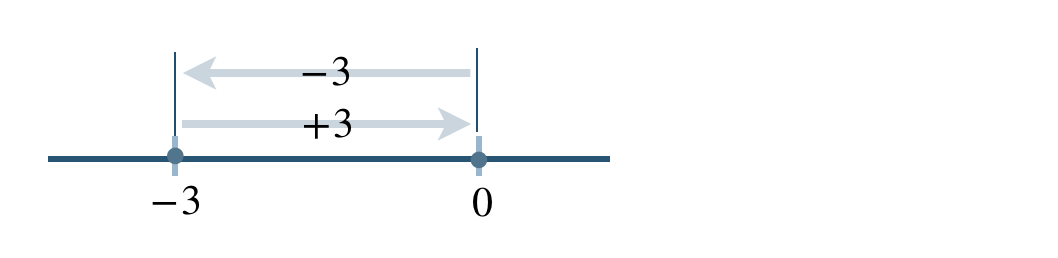
これより、
\((-3)+(+3)=0\)
したがって、答えは \(0\) となる
【別解】
異なる符号で絶対値が等しいので、答えは \(0\)
\((-3)+(+3)=0\)
したがって、答えは \(0\) となる
問題解説(8)
次の計算をせよ。
\({\small (8)}~~(-5)+(-9)\)
数直線上の移動で考えると、
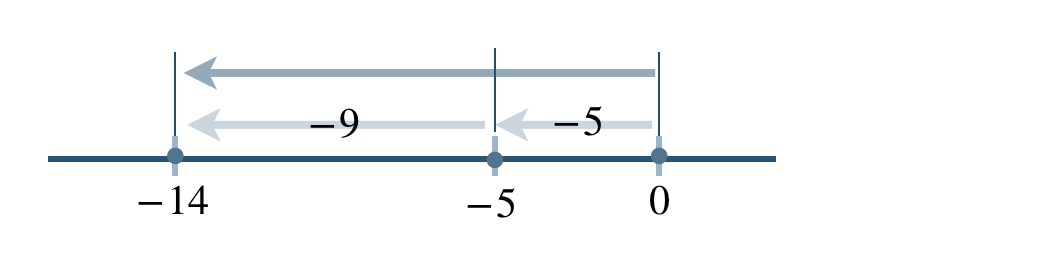
これより、
\((-5)+(-9)=-14\)
したがって、答えは \(-14\) となる
【別解】
同じ符号であるから、共通の符号で、絶対値の和より、
\(\begin{split}&(-5)+(-9)\\[2pt]~~=~&-(5+9)\\[2pt]~~=~&-14\end{split}\)
したがって、答えは \(-14\) となる



