加法の交換法則・結合法則

加法の交換法則・結合法則の解法

Point：加法の交換法則・結合法則

■ 加法の交換法則
正の数・負の数の加法では計算の順序を入れかえることができる。

$\begin{split}&(-4)+(+6)+(+4)\\[2pt]~~=~&(-4)+(+4)+(+6)\\[2pt]~~=~&0+(+6)\\[2pt]~~=~&+6\end{split}$

※ $(+6)$ と $(+4)$ を入れかえて計算。

■ 加法の結合法則
正の数・負の数の加法では計算の組合せをかえることができる。

$\begin{split}&(-4)+(+6)+(+4)\\[2pt]~~=~&(-4)+(6+4)\\[2pt]~~=~&(-4)+(+10)\\[2pt]~~=~&+(10-4)\\[2pt]~~=~&+6\end{split}$

※ $(+6)+(+4)$ を先に計算。

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

くふうして、次の計算をせよ。

${\small (1)}~~(-3)+(+8)+(+2)$

加法の結合法則より、 $(+8)+(+2)$ を先に計算すると、

$\begin{split}&(-3)+(+8)+(+2)\\[2pt]~~=~&(-3)+\left\{(+8)+(+2)\right\}\end{split}$

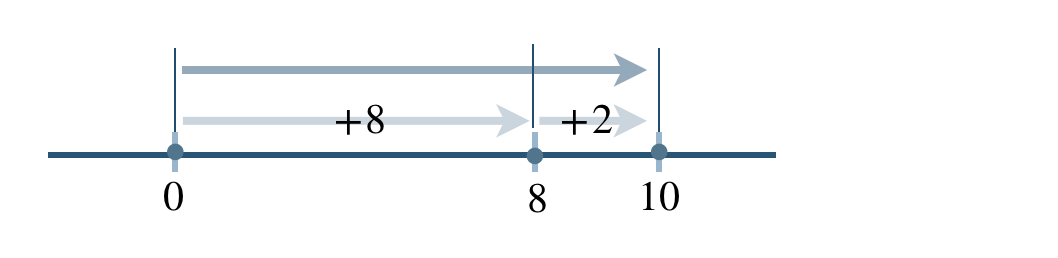
$\begin{split}~~=~&(-3)+(8+2)\\[2pt]~~=~&(-3)+(+10)\end{split}$

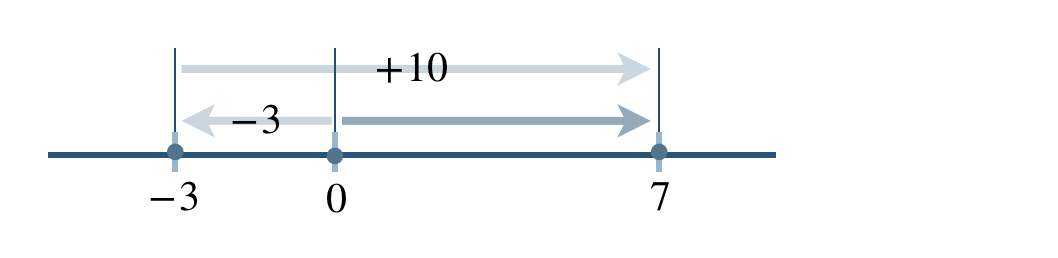
$\begin{split}~~=~&+(10-3)\\[2pt]~~=~&+7\end{split}$

したがって、答えは $+7$ となる

問題

くふうして、次の計算をせよ。

${\small (2)}~~(+12)+(-3)+(+8)+(-7)$

加法の交換法則より、正の数と負の数がとなりにくるように順序を入れかえると、

$\begin{split}&(+12)+(-3)+(+8)+(-7)\\[2pt]~~=~&(+12)+(+8)+(-3)+(-7)\end{split}$

加法の結合法則より、

$(+12)+(+8)$ と

$(-3)+(-7)$ をそれぞれ計算して、

$\begin{split}~=\{(+12)+(+8)\}+\{(-3)+(-7)\}\end{split}$

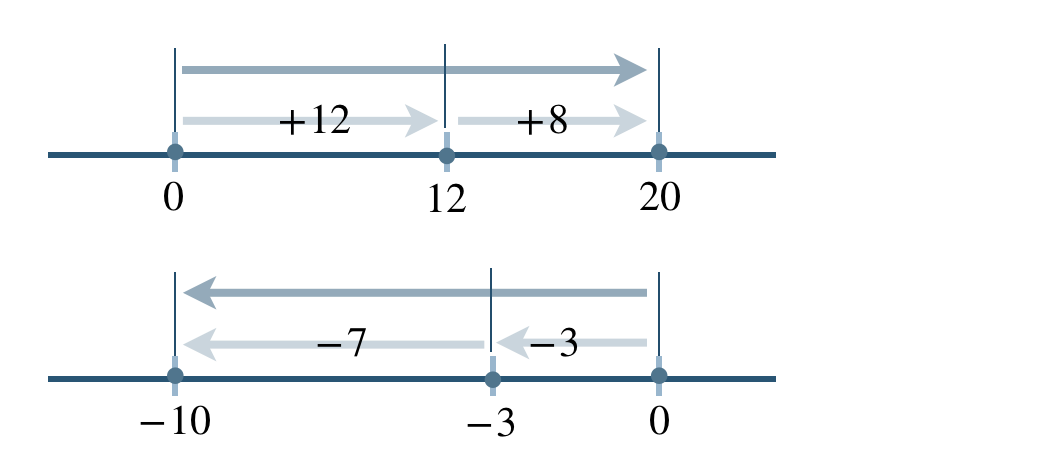
$\begin{split}~~=~&\{+(12+8)\}+\{-(3+7)\}\\[2pt]~~=~&(+20)+(-10)\end{split}$

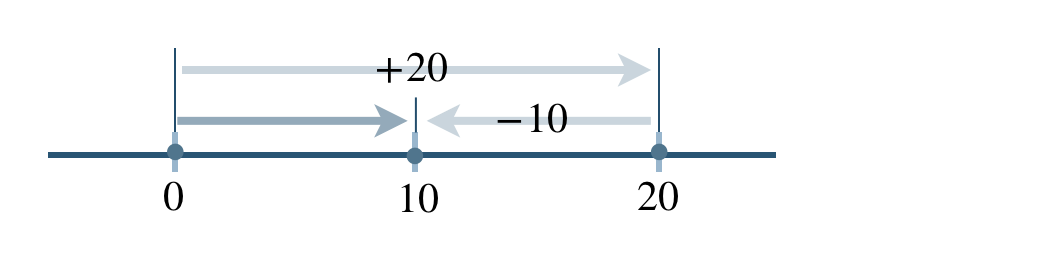
$\begin{split}~~=~&+(20-10)\\[2pt]~~=~&+10\end{split}$

したがって、答えは $+10$ となる

問題

くふうして、次の計算をせよ。

${\small (3)}~~(+4)+(+5)+(-1)+(-4)+(-9)$

加法の交換法則より、 $+4$ と $-4$ がとなりにくるように順序を入れかえると、

$\begin{split}&(+4)+(+5)+(-1)+(-4)+(-9)\\[2pt]~~=~&(+4)+(-4)+(+5)+(-1)+(-9)\end{split}$

加法の結合法則より、

$(+4)+(-4)$ と

$(-1)+(-9)$ をそれぞれ計算して、

$\begin{split}~=\{(+4)+(-4)\}+(+5)+\{(-1)+(-9)\}\end{split}$

$\begin{split}~~=~&0+(+5)+\{-(1+9)\}\\[2pt]~~=~&0+(+5)+(-10)\end{split}$

$\begin{split}~~=~&-(10-5)\\[2pt]~~=~&-5\end{split}$

したがって、答えは $-5$ となる