分数・小数の項をふくむ計算

Point：分数・小数の項をふくむ計算

分数や小数をふくんでいても、加法・減法の基本的な解き方は同じとなる。

---

① 減法を加法にする(反対の性質のことば)。
② (　)を外して、項だけの式にする。
③ 正の項と負の項に分ける(加法の交換法則)。
④ 加法の結合法則で正の項と負の項をそれぞれ計算して、さらに計算する。

---

※ 分数の計算では通分に注意する。

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次の計算をせよ。

---

\({\small (1)}~-1.7+0.6-0.7\)

加法の交換法則より、\(-1.7\) と \(+0.6\) を入れかえて、

---

\(\begin{split}&-1.7+0.6-0.7\\[2pt]~~=~&0.6-1.7-0.7\end{split}\)

---

加法の結合法則より、\(-1.7-0.7\) を先に計算すると、

---

\(\begin{split}~~=~&0.6-(1.7+0.7)\\[2pt]~~=~&0.6-2.4\end{split}\)

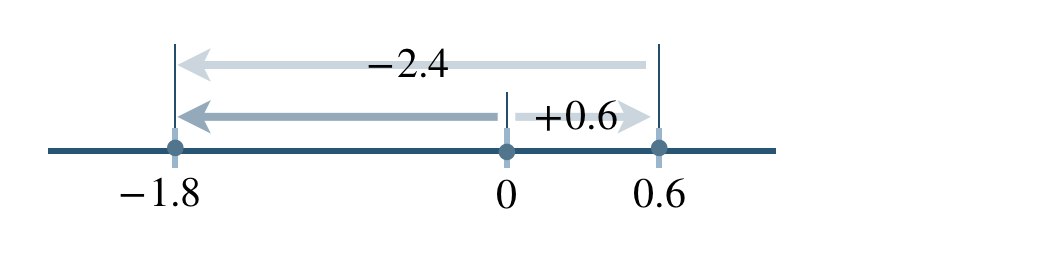
\(\begin{split}~~=~&-(2.4-0.6)\\[2pt]~~=~&-1.8\end{split}\)

---

したがって、答えは \(-1.8\) となる

問題

次の計算をせよ。

---

\({\small (2)}~(-1.5)-(-1.8)-(+2.3)\)

減法を加法にかえると、
負の数 \(-1.8\) を引き算することは、正の数 \(+1.8\) を足し算することであり、
正の数 \(+2.3\) を引き算することは、負の数 \(-2.3\) を足し算することであるので、

---

\(\begin{split}&(-1.5)-(-1.8)-(+2.3)\\[2pt]~~=~&(-1.5)+(+1.8)+(-2.3)\end{split}\)

---

項だけの式にすると、

---

\(\begin{split}~~=~&-1.5+1.8-2.3\end{split}\)

---

加法の交換法則より、\(-1.5\) と \(+1.8\) を入れかえて、

---

\(\begin{split}~~=~&1.8-1.5-2.3\end{split}\)

---

加法の結合法則より、\(-1.5-2.3\) を先に計算すると、

---

\(\begin{split}~~=~&1.8-(1.5+2.3)\\[2pt]~~=~&1.8-3.8\end{split}\)

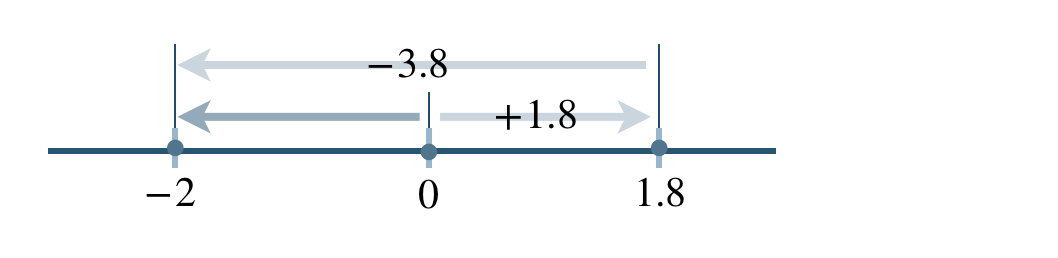
\(\begin{split}~~=~&-(3.8-1.8)\\[2pt]~~=~&-2\end{split}\)

---

したがって、答えは \(-2\) となる

問題

次の計算をせよ。

---

\({\small (3)}~\)\(\begin{split}\frac{\,1\,}{\,6\,}-\left(-\frac{\,1\,}{\,2\,}\right)-\left(+\frac{\,1\,}{\,3\,}\right)\end{split}\)

---

減法を加法にかえると、

---

負の数 \(\begin{split}-{ \frac{\,1\,}{\,2\,}}\end{split}\) を引き算することは、正の数 \(\begin{split}+{ \frac{\,1\,}{\,2\,}}\end{split}\) を足し算することであり、

---

正の数 \(\begin{split}+{ \frac{\,1\,}{\,3\,}}\end{split}\) を引き算することは、負の数 \(\begin{split}-{ \frac{\,1\,}{\,3\,}}\end{split}\) を足し算することであるので、

---

\(\begin{split}&\frac{\,1\,}{\,6\,}-\left(-\frac{\,1\,}{\,2\,}\right)-\left(+\frac{\,1\,}{\,3\,}\right)\\[3pt]~~=~&\frac{\,1\,}{\,6\,}+\left(+\frac{\,1\,}{\,2\,}\right)+\left(-\frac{\,1\,}{\,
3\,}\right)\end{split}\)

---

項だけの式にすると、

---

\(\begin{split}~~=~&\frac{\,1\,}{\,6\,}+\frac{\,1\,}{\,2\,}-\frac{\,1\,}{\,3\,}\end{split}\)

---

通分すると、

---

\(\begin{split}~~=~&\frac{\,1\,}{\,6\,}+\frac{\,1{\, \small \times \,}3\,}{\,2{\, \small \times \,}3\,}-\frac{\,1{\, \small \times \,}2\,}{\,3{\, \small \times \,}2\,}\\[3pt]~~=~&\frac{\,1\,}{\,6\,}+\frac{\,3\,}{\,6\,}-\frac{\,2\,}{\,6\,}\\[3pt]~~=~&
\frac{\,1+3-2\,}{\,6\,}\end{split}\)

---

加法の結合法則より、分子の \(1+3\) を先に計算すると、

---

\(\begin{split}~~=~&\frac{\,(1+3)-2\,}{\,6\,}\\[3pt]~~=~&\frac{\,4-2\,}{\,6\,}\\[3pt]~~=~&\frac
{\,2\,}{\,6\,}\end{split}\)

---

約分すると、

---

\(\require{cancel} \begin{split}~~=~&\frac{\,\cancel{2}
^{1}\,}{\,\cancel{6}^{3}\,}\\[3pt]~~=~&\frac{\,1\,}{\,3\,}\end{split}\)

したがって、答えは \(\begin{split}{ \frac{\,1\,}{\,3\,}}\end{split}\) となる

問題

次の計算をせよ。

---

\({\small (4)}~\)\(\begin{split}1+\left(-\frac{\,3\,}{\,5\,}\right)-\left(-\frac{\,1\,}{\,2\,}\right)-\frac{\,9\,}{\,10\,}\end{split}\)

---

減法を加法にかえると、

---

負の数 \(\begin{split}-{ \frac{\,1\,}{\,2\,}}\end{split}\) を引き算することは、正の数 \(\begin{split}+{ \frac{\,1\,}{\,2\,}}\end{split}\) を足し算することであるので、

---

\(\begin{split}&1+\left(-\frac{\,3\,}{\,5\,}\right)-\left(-\frac{\,1\,}{\,2\,}\right)-\frac{\,9\,}{\,10\,}\\[3pt]~~=~&1+\left(-\frac{\,3\,}{\,5\,}\right)+\left(+\frac{\,1\,}{\,2\,}\right)
-\frac{\,9\,}{\,10\,}\end{split}\)

---

項だけの式にすると、

---

\(\begin{split}~~=~&1-\frac{\,3\,}{\,5\,}+\frac{\,1\,}{\,2\,}-\frac{\,9\,}{\,10\,}\end{split}\)

---

通分すると、

---

\(\begin{split}~~=~&\frac{\,1{\, \small \times \,}10\,}{\,1{\, \small \times \,}10\,}-\frac{\,3{\, \small \times \,}2\,}{\,5{\, \small \times \,}2\,}+\frac{\,1{\, \small \times \,}5\,}{\,2{\, \small \times \,}5\,}-\frac{\,9\,}{\,10\,}\\[3pt]~~=~&\frac{\,10\,}{\,10\,}-\frac{\,6\,}{\,10\,}+\frac{\,5\,}{\,10\,}-\frac{\,9\,}{\,10\,}\\[3pt]~~=~&\frac{\,10-6+5-9\,}{\,10\,}\end
{split}\)

---

加法の交換法則より、分子の \(-6\) と \(5\) を入れかえて、

---

\(\begin{split}~~=~&\frac{\,10+5-6-9\,}{\,10\,}\end{split}\)

---

加法の結合法則より、分子の正の数 \(10+5\) と負の数 \(-6-9\) をそれぞれ計算すると、

---

\(\begin{split}~~=~&\frac{\,(10+5)-(6+9)\,}{\,10\,}\\[3pt]~~=~&\frac{\,15-15\,}{\,10\,}\\[3pt]
~~=~&\frac{\,0\,}{\,10\,}\\[3pt]~~=~&0\end{split}\)

---

したがって、答えは \(0\) となる