変数と関数の解法
Point:変数と関数
たとえば、\(1\) 個 \(3~{\rm g}\) のアメがあり、\(x\) 個の重さ \(y~{\rm g}\) とすると、
\(x=1\) のとき、\(y=3{\, \small \times \,}1=3~{\rm g}\)
\(x=2\) のとき、\(y=3{\, \small \times \,}2=6~{\rm g}\)
\(x=3\) のとき、\(y=3{\, \small \times \,}3=9~{\rm g}\)
\(x=4\) のとき、\(y=3{\, \small \times \,}4=12~{\rm g}\)
\(x=5\) のとき、\(y=3{\, \small \times \,}5=15~{\rm g}\)
いろいろな値をとる文字を「変数」という。
2つの変数 \(x~,~y\) について、
\(x\) の値を決めると、それに対応して \(y\) の値がただ1つに決まるとき、「 \(y\) は \(x\) の関数」という。
たとえば、\(1\) 個 \(3~{\rm g}\) のアメがあり、\(x\) 個の重さ \(y~{\rm g}\) とすると、
\(x=1\) のとき、\(y=3{\, \small \times \,}1=3~{\rm g}\)
\(x=2\) のとき、\(y=3{\, \small \times \,}2=6~{\rm g}\)
\(x=3\) のとき、\(y=3{\, \small \times \,}3=9~{\rm g}\)
\(x=4\) のとき、\(y=3{\, \small \times \,}4=12~{\rm g}\)
\(x=5\) のとき、\(y=3{\, \small \times \,}5=15~{\rm g}\)
| \(x\) 個 | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| \(y~{\rm g}\) | \(3\) | \(6\) | \(9\) | \(12\) | \(15\) |
このように、\(x\) の値を決めると、それに対応して \(y\) の値がただ1つに決まるので、\(y\) は \(x\) の関数といえる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:変数と関数
問題解説(1)
問題
\({\small (1)}~\)次の①〜⑥のうち、\(y\) が \(x\) の関数であるものを答えよ。
① 半径 \(x~{\rm cm}\) の円の面積が \(y~{\rm cm}^2\)。
② \(20~{\rm km}\) の道のりを時速 \(x~{\rm km}\) で走ると \(y\) 時間かかる。
③ \(x\) 歳の人の身長は \(y~{\rm cm}\)。
④ 周の長さ \(20~{\rm cm}\) の長方形の縦の長さ \(x~{\rm cm}\) と横の長さ \(y~{\rm cm}\)。
⑤ 整数 \(x\) の絶対値が \(y\)。
⑥ 周りの長さ \(x~{\rm cm}\) の長方形の面積が \(y~{\rm cm}^2\)。
次の問いに答えよ。
\({\small (1)}~\)次の①〜⑥のうち、\(y\) が \(x\) の関数であるものを答えよ。
① 半径 \(x~{\rm cm}\) の円の面積が \(y~{\rm cm}^2\)。
② \(20~{\rm km}\) の道のりを時速 \(x~{\rm km}\) で走ると \(y\) 時間かかる。
③ \(x\) 歳の人の身長は \(y~{\rm cm}\)。
④ 周の長さ \(20~{\rm cm}\) の長方形の縦の長さ \(x~{\rm cm}\) と横の長さ \(y~{\rm cm}\)。
⑤ 整数 \(x\) の絶対値が \(y\)。
⑥ 周りの長さ \(x~{\rm cm}\) の長方形の面積が \(y~{\rm cm}^2\)。
① 半径 \(x~{\rm cm}\) の円の面積が \(y~{\rm cm}^2\)。
半径が \(x=1~{\rm cm}\) のとき、円の面積 \(y~{\rm cm}^2\) は、
\(\begin{split}~~~y=1{\, \small \times \,}1{\, \small \times \,} \pi=\pi~{\rm cm}^2\end{split}\)
半径が \(x=2~{\rm cm}\) のとき、円の面積 \(y~{\rm cm}^2\) は、
\(\begin{split}~~~y=2{\, \small \times \,}2{\, \small \times \,} \pi=4\pi~{\rm cm}^2\end{split}\)
これより、\(x\) の値を決めると、それに対応して \(y\) の値がただ1つに決まるので、\(y\) は \(x\) の関数といえる
② \(20~{\rm km}\) の道のりを時速 \(x~{\rm km}\) で走ると \(y\) 時間かかる。
時速 \(2~{\rm km}\) のときの時間 \(y\) は、道のり÷速さより、
\(\begin{split}~~~20{\, \small \div \,}2=10\end{split}\)
時速 \(5~{\rm km}\) のときの時間 \(y\) は、道のり÷速さより、
\(\begin{split}~~~20{\, \small \div \,}5=4\end{split}\)
これより、\(x\) の値を決めると、それに対応して \(y\) の値がただ1つに決まるので、\(y\) は \(x\) の関数といえる
③ \(x\) 歳の人の身長は \(y~{\rm cm}\)。
\(x=14\) のとき、\(14\) 歳の人の身長は人によって変わるので \(y\) の値は1つに決まらない
これより、\(x\) の値を決めても、それに対応して \(y\) の値がただ1つに決まらないので、\(y\) は \(x\) の関数といえない
④ 周の長さ \(20~{\rm cm}\) の長方形の縦の長さ \(x~{\rm cm}\) と横の長さ \(y~{\rm cm}\)。
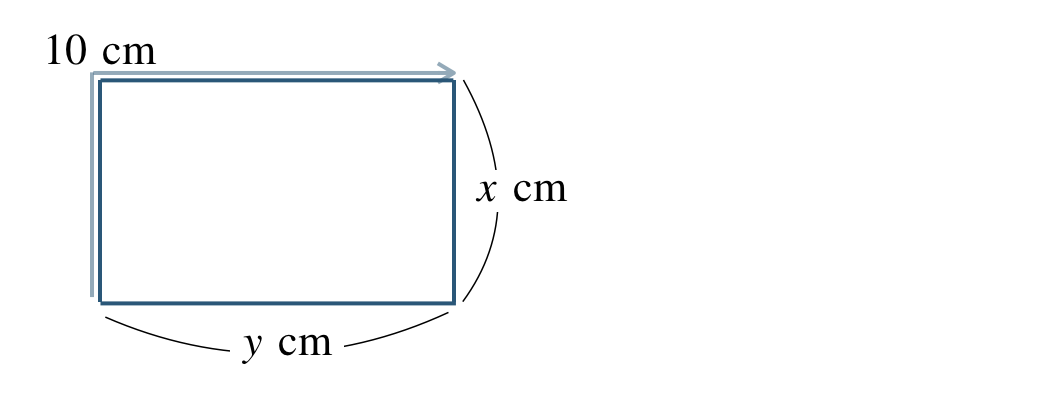
図より、縦の長さと横の長さの和が \(10~{\rm cm}\) となる
縦の長さ \(x=2~{\rm cm}\) と横の長さ \(y~{\rm cm}\) は、
\(\begin{split}~~~y=10-2=8~{\rm cm}\end{split}\)
縦の長さ \(x=4~{\rm cm}\) と横の長さ \(y~{\rm cm}\) は、
\(\begin{split}~~~y=10-4=6~{\rm cm}\end{split}\)
これより、\(x\) の値を決めると、それに対応して \(y\) の値がただ1つに決まるので、\(y\) は \(x\) の関数といえる
⑤ 整数 \(x\) の絶対値が \(y\)。
整数 \(x=3\) の絶対値は \(y=3\) となる
整数 \(x=-5\) の絶対値は \(y=5\) となる
これより、\(x\) の値を決めると、それに対応して \(y\) の値がただ1つに決まるので、\(y\) は \(x\) の関数といえる
⑥ 周りの長さ \(x~{\rm cm}\) の長方形の面積が \(y~{\rm cm}^2\)。
周りの長さを \(x=30~{\rm cm}\) としたとき、
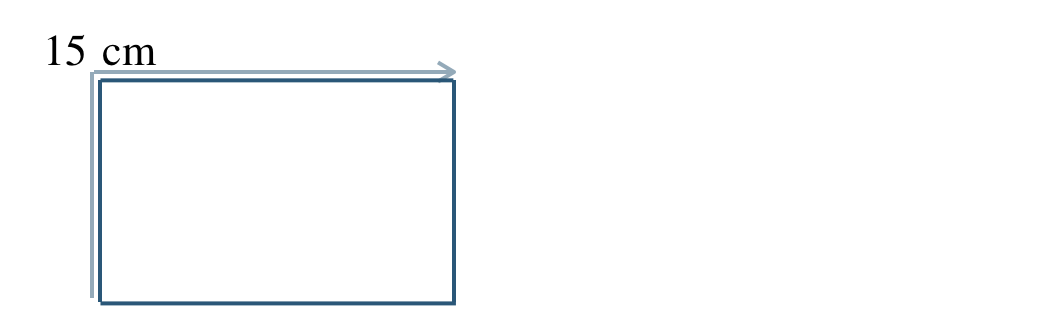
図より、縦の長さと横の長さの和が \(15~{\rm cm}\) となる
長方形の面積が \(y~{\rm cm}^2\) は、
縦の長さ \(10~{\rm cm}\) 、横の長さ \(5~{\rm cm}\) のとき、
\(\begin{split}~~~y=10{\, \small \times \,}5=50~{\rm cm}^2\end{split}\)
縦の長さ \(8~{\rm cm}\) 、横の長さ \(7~{\rm cm}\) のとき、
\(\begin{split}~~~y=8{\, \small \times \,}7=56~{\rm cm}^2\end{split}\)
これより、\(x\) の値を決めても、それに対応して \(y\) の値がただ1つに決まらないので、\(y\) は \(x\) の関数といえない
問題解説(2)
問題
\({\small (2)}~\)深さ \(30~{\rm cm}\) の空の水そうに \(1\) 分間で高さが \(5~{\rm cm}\) 高くなるように水を入れる。水を入れはじめてから \(x\) 分後の水の高さ \(y~{\rm cm}\) の関係の表を完成させよ。
次の問いに答えよ。
\({\small (2)}~\)深さ \(30~{\rm cm}\) の空の水そうに \(1\) 分間で高さが \(5~{\rm cm}\) 高くなるように水を入れる。水を入れはじめてから \(x\) 分後の水の高さ \(y~{\rm cm}\) の関係の表を完成させよ。
| \(x\) 分 | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(y~{\rm cm}\) | \(5\) |
\(1\) 分間で高さが \(5~{\rm cm}\) 高くなるので、
\(x=1\) 分後の水の高さ \(y~{\rm cm}\) は、
\(\begin{split}~~~y=5{\, \small \times \,} 1=5~{\rm cm}\end{split}\)
\(x=2\) 分後の水の高さ \(y~{\rm cm}\) は、
\(\begin{split}~~~y=5{\, \small \times \,} 2=10~{\rm cm}\end{split}\)
\(x=3\) 分後の水の高さ \(y~{\rm cm}\) は、
\(\begin{split}~~~y=5{\, \small \times \,} 3=15~{\rm cm}\end{split}\)
\(x=4\) 分後の水の高さ \(y~{\rm cm}\) は、
\(\begin{split}~~~y=5{\, \small \times \,} 4=20~{\rm cm}\end{split}\)
\(x=5\) 分後の水の高さ \(y~{\rm cm}\) は、
\(\begin{split}~~~y=5{\, \small \times \,} 5=25~{\rm cm}\end{split}\)
\(x=6\) 分後の水の高さ \(y~{\rm cm}\) は、
\(\begin{split}~~~y=5{\, \small \times \,} 6=30~{\rm cm}\end{split}\)
したがって、
| \(x\) 分 | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(y~{\rm cm}\) | \(5\) | \(10\) | \(15\) | \(20\) | \(25\) | \(30\) |
となる

【問題一覧】中1|比例と反比例
このページは「中学数学1 比例と反比例」の問題一覧ページとなります。解説の見たい単元名がわからないと...


