座標と点の表し方の解法
点 \({\rm O}\) で垂直に交わる2本の数直線について、
横の数直線を「 \(x\) 軸(横軸)」
縦の数直線を「 \(y\) 軸(縦軸)」
\(x\) 軸と \(y\) 軸を合わせて「座標軸」
点 \({\rm O}\) を「原点」 という。
■ 点の座標
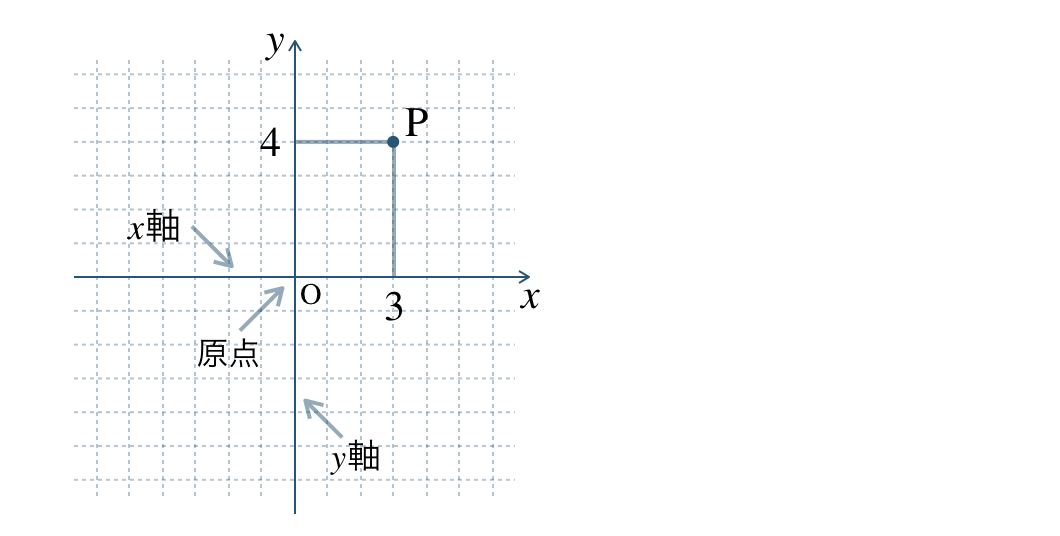
上の図の点 \({\rm P}\) について、
点 \({\rm P}\) から \(x\) 軸、\(y\) 軸にそれぞれ垂直な直線をひいたとき、
\(x\) 軸上のめもりは \(3\)、\(y\) 軸上のめもりは \(4\)
の位置にあるので、点 \({\rm P}\) を \({\rm P}(3~,~4)\) と表す。
この \({\rm P}(3~,~4)\) を「座標」といい、
\(3\) を「\(x\) 座標」、\(4\) を「\(y\) 座標」という。
※ 点 \({\rm P}\) は原点 \({\rm O}\) から右に \(3\)、上に \(4\) 進んだ点と考えることができる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:座標と点の表し方
問題解説(1)
次の問いに答えよ。
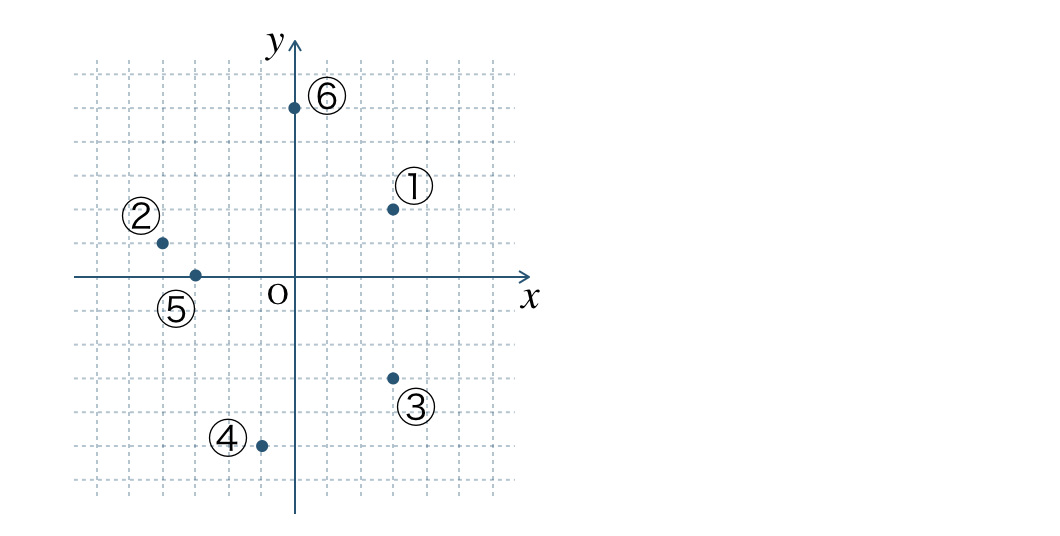
\({\small (1)}~\)次の点①〜⑥の座標を答えよ。
①
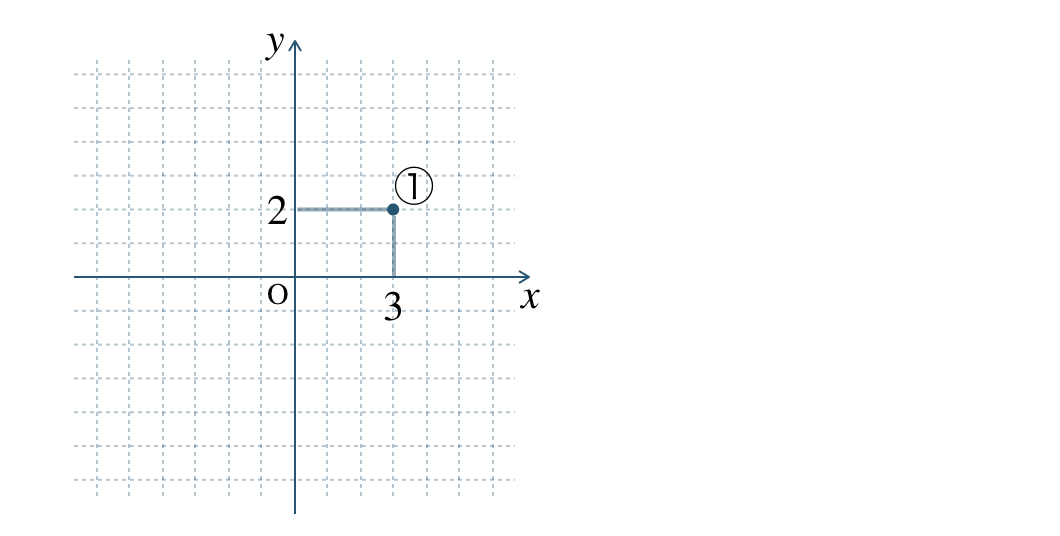
図より、\(x\) 座標 \(3\) で \(y\) 座標 \(2\) となるので、
①の座標は、\((3~,~2)\) となる
②
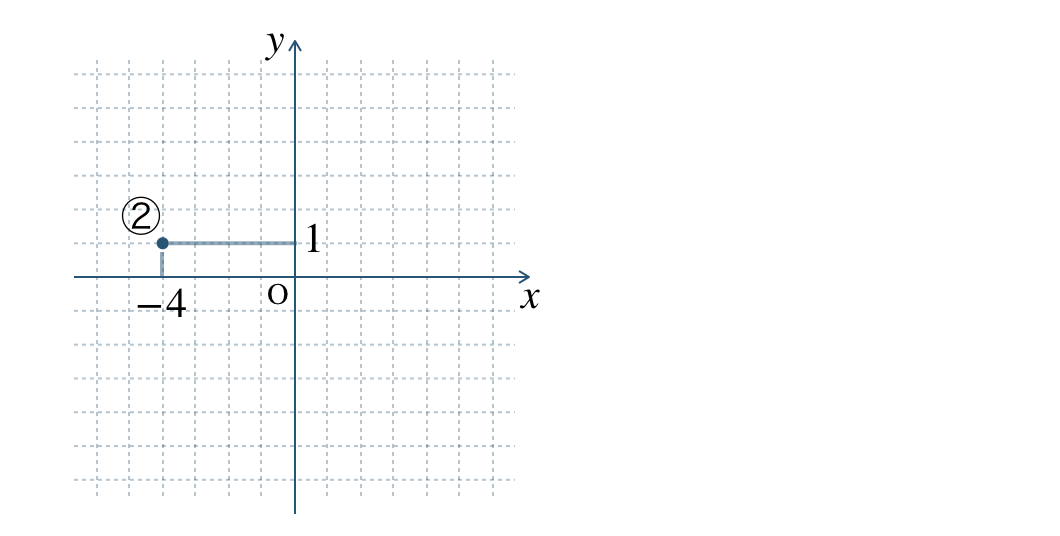
図より、\(x\) 座標 \(-4\) で \(y\) 座標 \(1\) となるので、
②の座標は、\((-4~,~1)\) となる
③
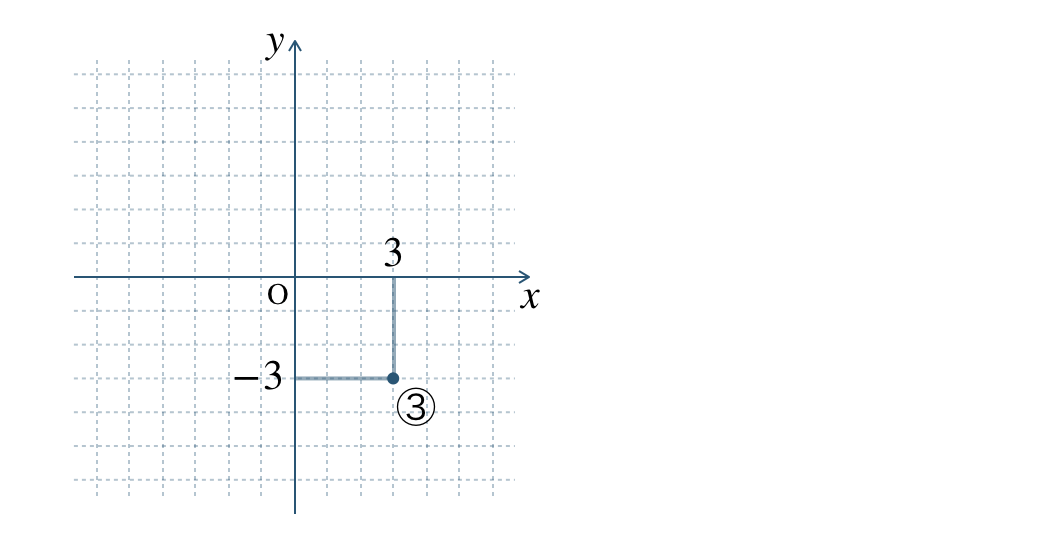
図より、\(x\) 座標 \(3\) で \(y\) 座標 \(-3\) となるので、
③の座標は、\((3~,~-3)\) となる
④
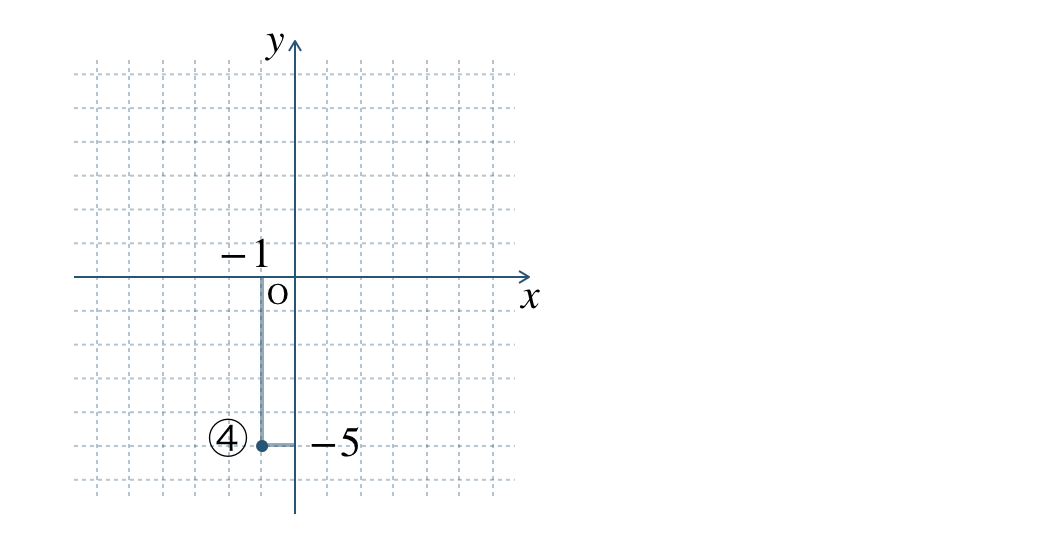
図より、\(x\) 座標 \(-1\) で \(y\) 座標 \(-5\) となるので、
④の座標は、\((-1~,~-5)\) となる
⑤
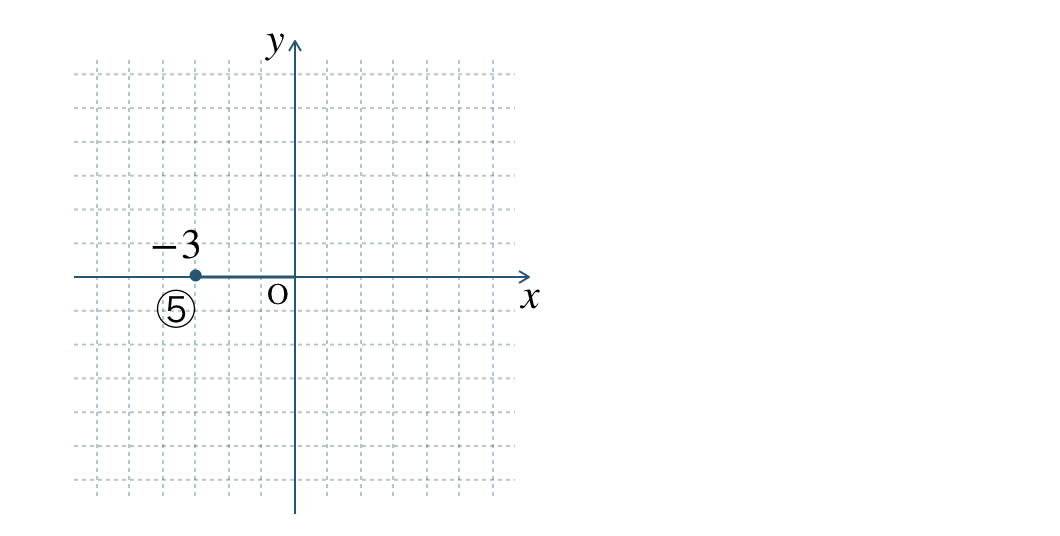
図より、\(x\) 座標 \(-3\) で \(y\) 座標 \(0\) となるので、
⑤の座標は、\((-3~,~0)\) となる
⑥
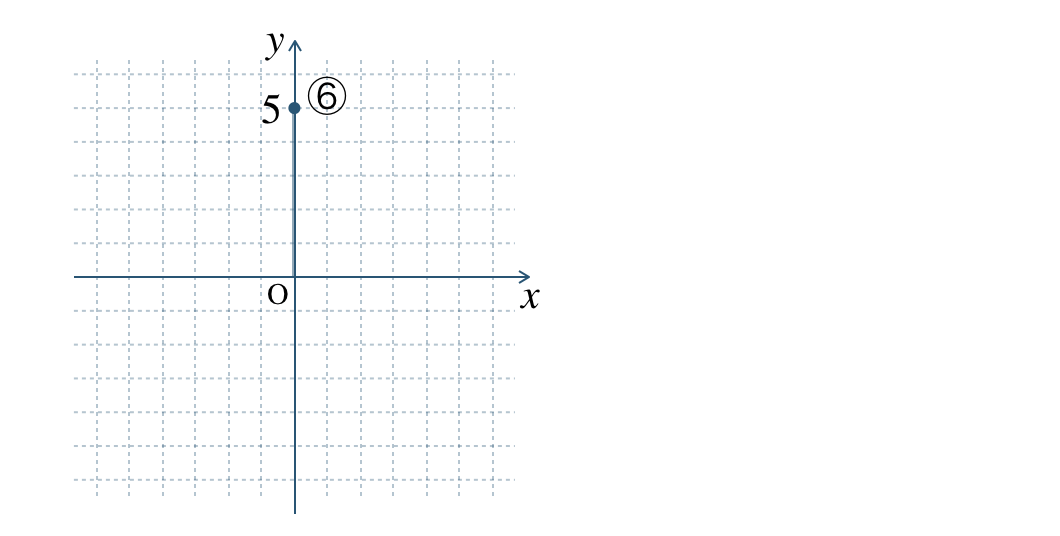
図より、\(x\) 座標 \(0\) で \(y\) 座標 \(5\) となるので、
⑥の座標は、\((0~,~5)\) となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の点を図にかき入れよ。
① \(\begin{split}(4~,~3)\end{split}\)
② \(\begin{split}(-3~,~5)\end{split}\)
③ \(\begin{split}(1~,~-5)\end{split}\)
④ \(\begin{split}(-2~,~-4)\end{split}\)
⑤ \(\begin{split}(3~,~0)\end{split}\)
⑥ \(\begin{split}(0~,~-2)\end{split}\)
① \(\begin{split}(4~,~3)\end{split}\)
座標より、\(x\) 座標 \(4\) で \(y\) 座標 \(3\) となるので、
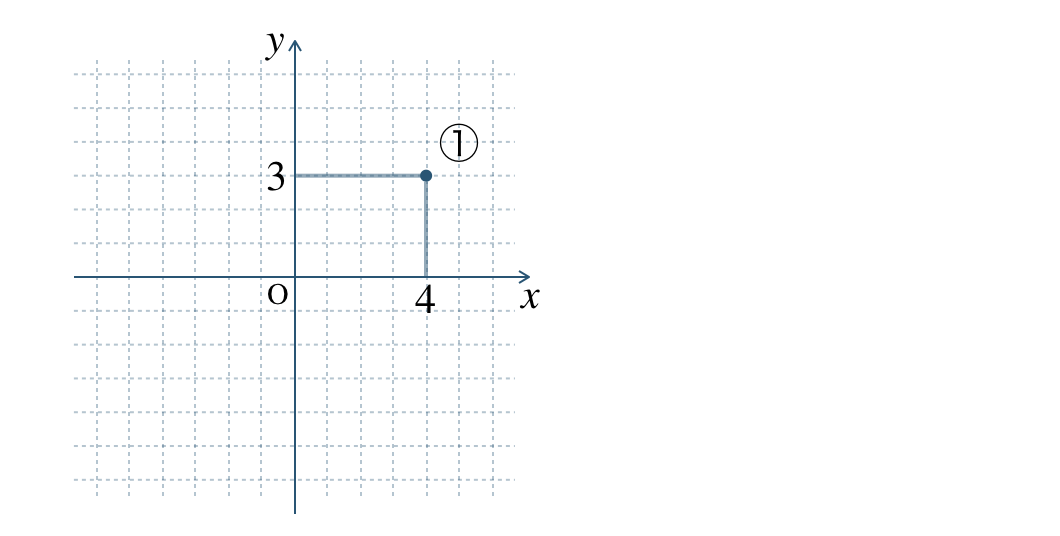
※ 原点 \({\rm O}\) から右に \(4\)、上に \(3\) 進んだ点と考える。
② \(\begin{split}(-3~,~5)\end{split}\)
座標より、\(x\) 座標 \(-3\) で \(y\) 座標 \(5\) となるので、
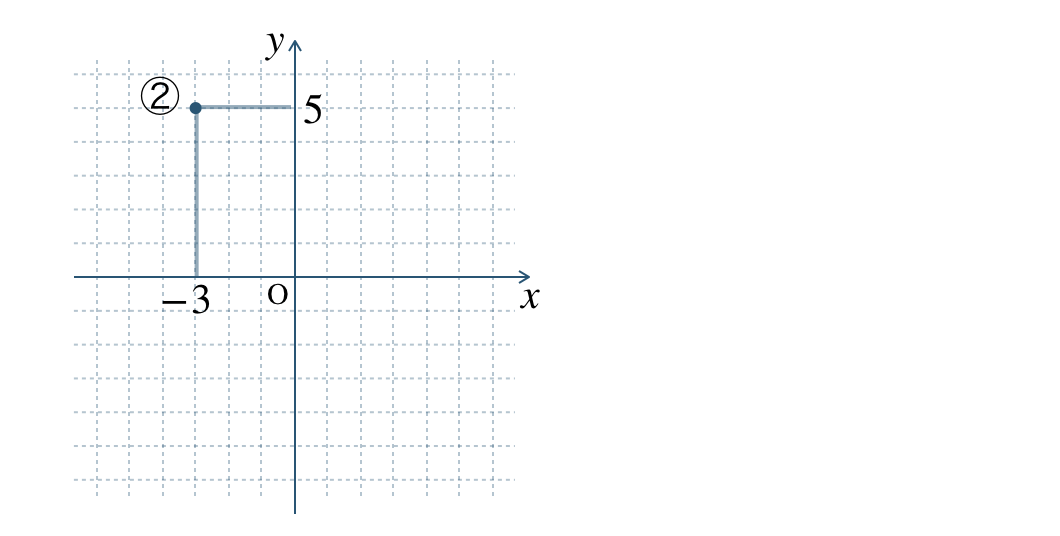
※ 原点 \({\rm O}\) から左に \(3\)、上に \(5\) 進んだ点と考える。
③ \(\begin{split}(1~,~-5)\end{split}\)
座標より、\(x\) 座標 \(1\) で \(y\) 座標 \(-5\) となるので、
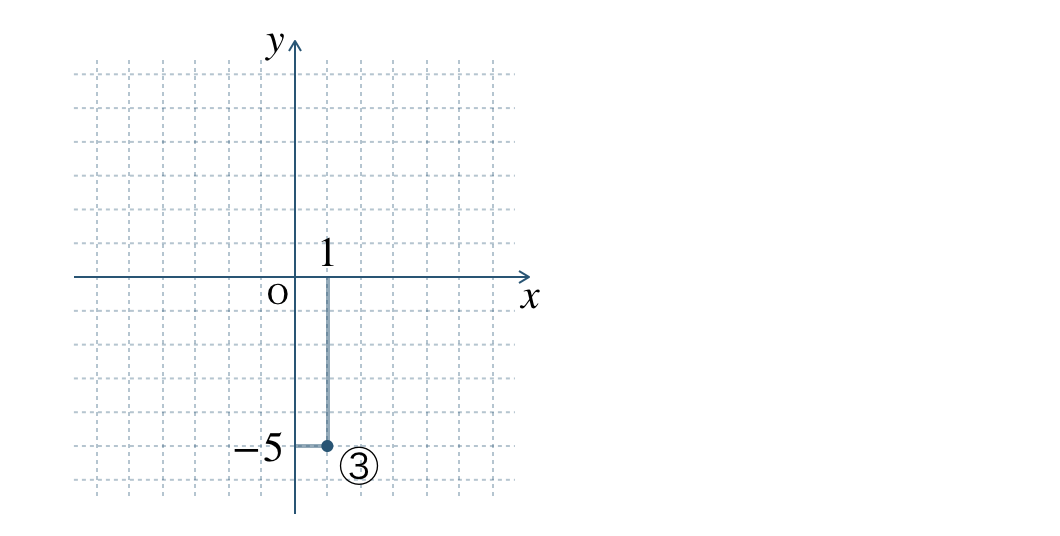
※ 原点 \({\rm O}\) から右に \(1\)、下に \(5\) 進んだ点と考える。
④ \(\begin{split}(-2~,~-4)\end{split}\)
座標より、\(x\) 座標 \(-2\) で \(y\) 座標 \(-4\) となるので、
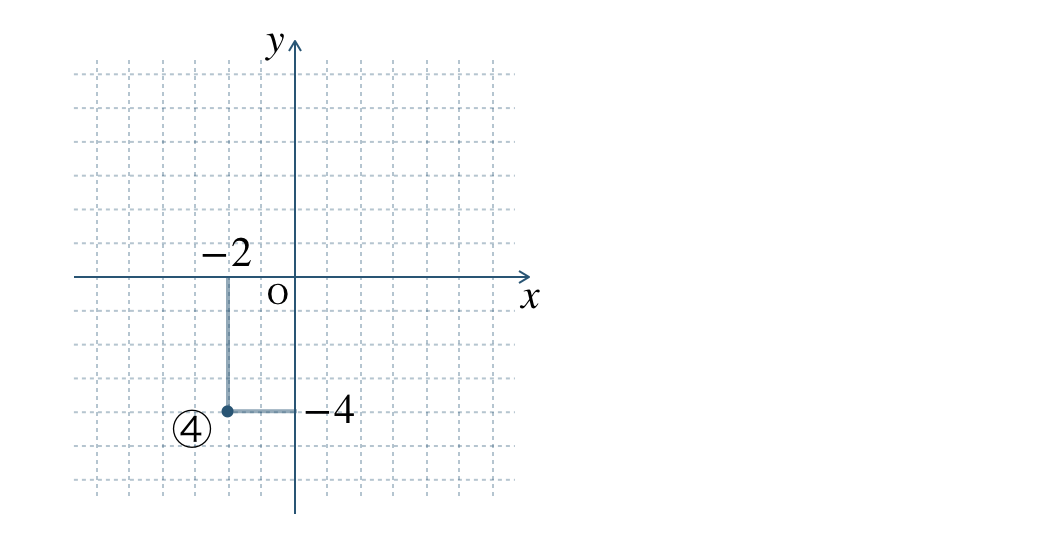
※ 原点 \({\rm O}\) から左に \(2\)、下に \(4\) 進んだ点と考える。
⑤ \(\begin{split}(3~,~0)\end{split}\)
座標より、\(x\) 座標 \(3\) で \(y\) 座標 \(0\) となるので、
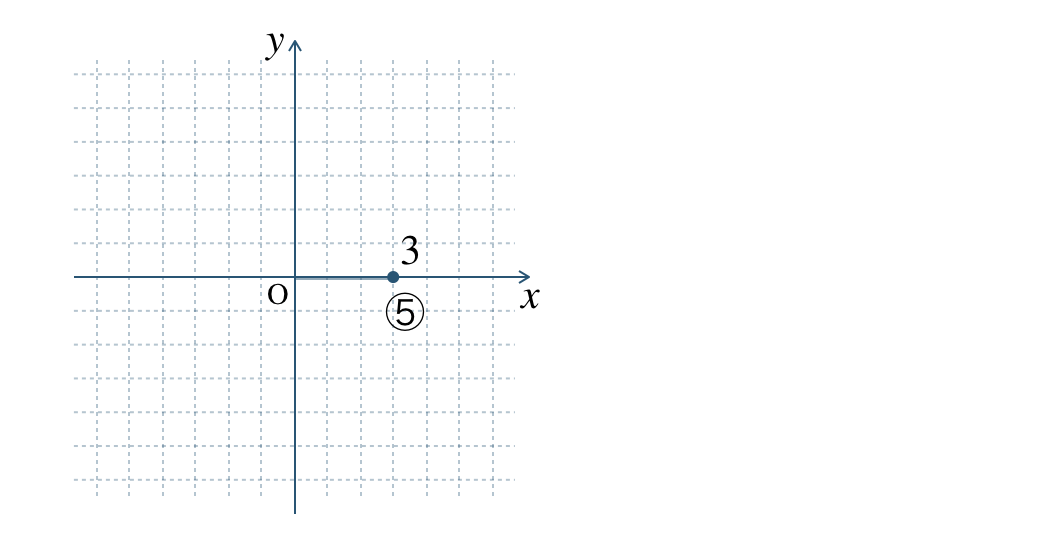
※ 原点 \({\rm O}\) から右に \(3\) 進んだ点と考える。
⑥ \(\begin{split}(0~,~-2)\end{split}\)
座標より、\(x\) 座標 \(0\) で \(y\) 座標 \(-2\) となるので、
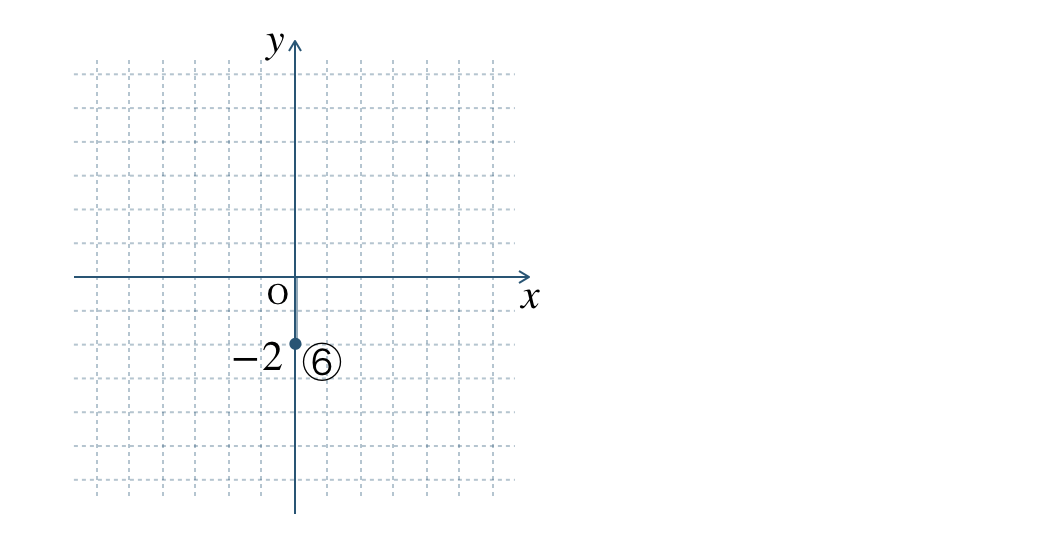
※ 原点 \({\rm O}\) から下に \(2\) 進んだ点と考える。



