反比例のグラフの解法
Point:反比例のグラフ
■ \(\begin{split}y={\frac{\,a\,}{\,x\,}}\end{split}\) のグラフ
\({\small (1)}~a>0\) のとき、
\(x\) が増加するとき \(y\) は減少する。
\({\small (2)}~a<0\) のとき、
\(x\) が増加するとき \(y\) も増加する。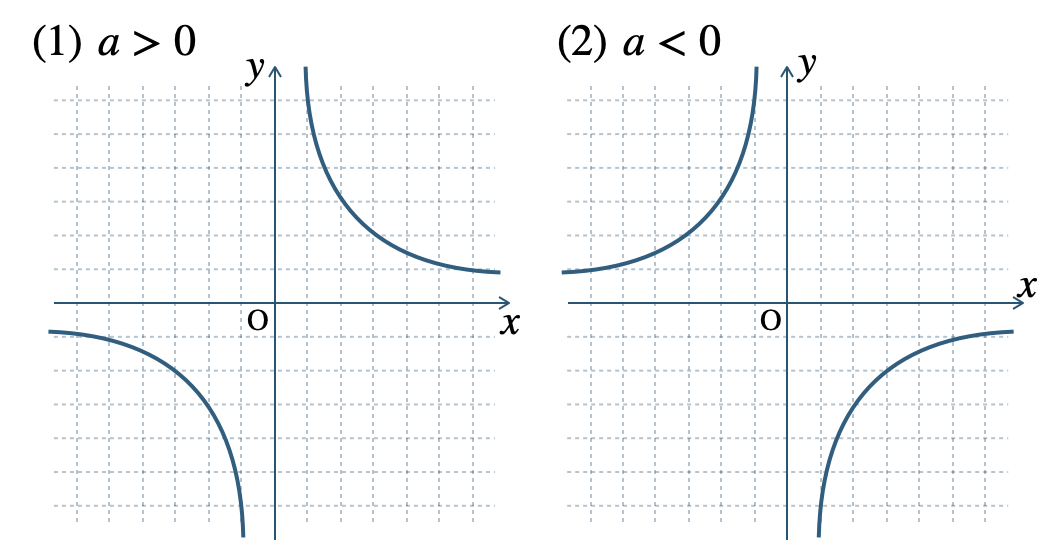
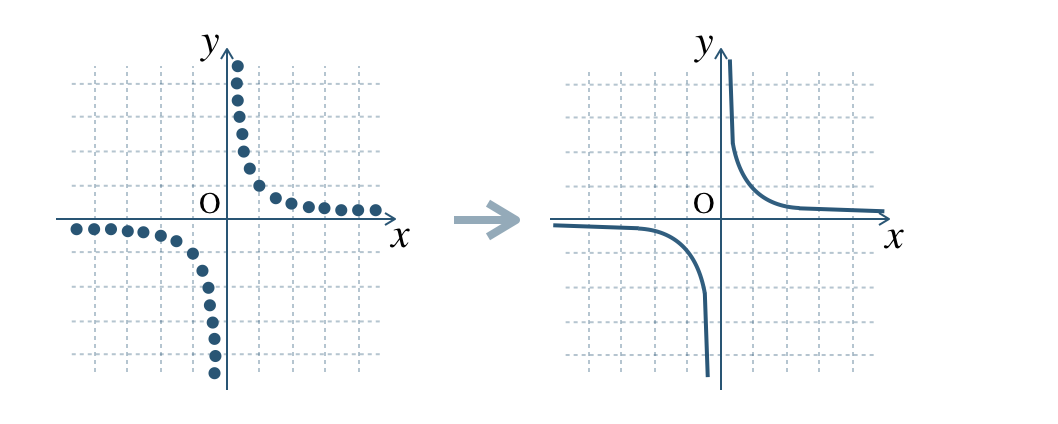
反比例の関係にある \(x\) と \(y\) について、
対応する点の座標を多くとっていくと、その集まりが曲線となる。この曲線を「双曲線」という。

※ グラフは \(x\) 軸、 \(y\) 軸と交わらない。
■ \(\begin{split}y={\frac{\,a\,}{\,x\,}}\end{split}\) のグラフ
\({\small (1)}~a>0\) のとき、
\(x\) が増加するとき \(y\) は減少する。
\({\small (2)}~a<0\) のとき、
\(x\) が増加するとき \(y\) も増加する。

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:反比例のグラフのかき方
\(\begin{split}y={\frac{\,4\,}{\,x\,}}\end{split}\) のグラフは、
① 反比例の式より、対応する整数 \(x\) と整数 \(y\) をいくつか書き出す。
※ \(x=0\) のときの \(y\) の値はない。
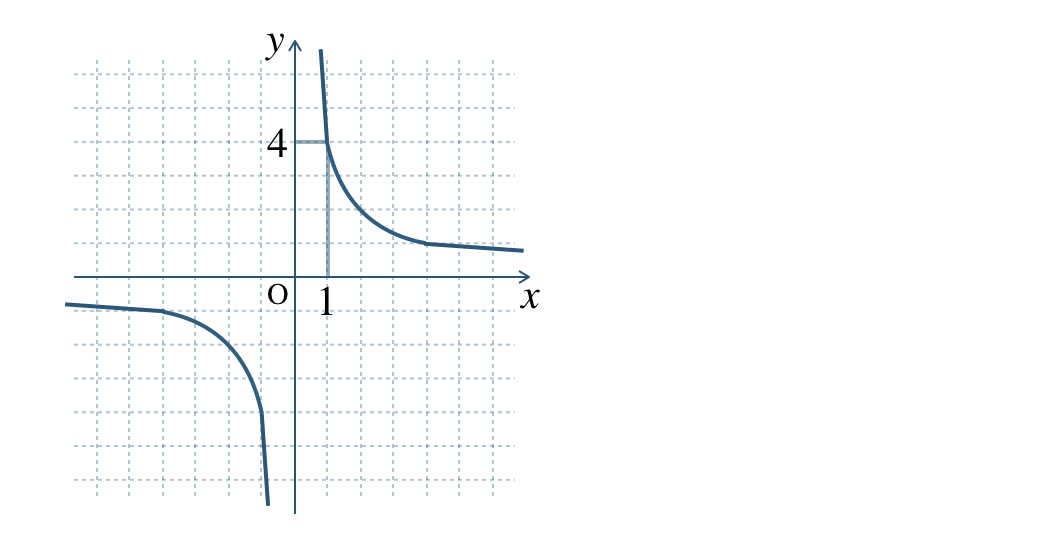
\(\begin{split}y={\frac{\,4\,}{\,x\,}}\end{split}\) のグラフは、
① 反比例の式より、対応する整数 \(x\) と整数 \(y\) をいくつか書き出す。
※ \(x=0\) のときの \(y\) の値はない。
| \(x\) | \(-4\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(4\) |
| \(y\) | \(-1\) | \(-2\) | \(-4\) | × | \(4\) | \(2\) | \(1\) |
② 対応する \(x\) と \(y\) の組を座標とする点をとり、なめらかな曲線をひく。

※ グラフは \(x\) 軸、 \(y\) 軸と交わらない。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:反比例のグラフ
問題解説(1)
問題
\(\begin{split}{\small (1)}~y=\frac{\,6\,}{\,x\,}\end{split}\)
次の反比例のグラフかけ。
\(\begin{split}{\small (1)}~y=\frac{\,6\,}{\,x\,}\end{split}\)
\(x=-6~,~-3~,~-2~,~-1~,~1~,~2~,~3~,~6\) のときの \(y\) の値をまとめると、
| \(x\) | \(-6\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(6\) |
| \(y\) | \(-1\) | \(-2\) | \(-3\) | \(-6\) | × | \(6\) | \(3\) | \(2\) | \(1\) |
※ \(x\) も \(y\) も整数となる組をとる。
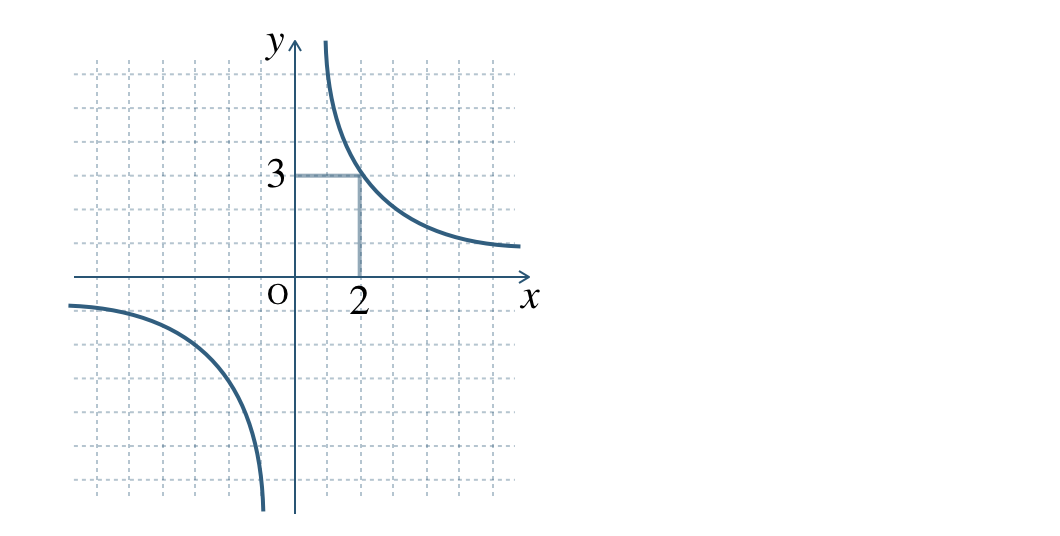
対応する \(x\) と \(y\) の組を座標とする点をとり、なめらかな曲線をひくと、
※ グラフは \(x\) 軸、 \(y\) 軸と交わらない。
問題解説(2)
問題
\(\begin{split}{\small (2)}~y=-\frac{\,6\,}{\,x\,}\end{split}\)
次の反比例のグラフかけ。
\(\begin{split}{\small (2)}~y=-\frac{\,6\,}{\,x\,}\end{split}\)
\(x=-6~,~-3~,~-2~,~-1~,~1~,~2~,~3~,~6\) のときの \(y\) の値をまとめると、
| \(x\) | \(-6\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(6\) |
| \(y\) | \(1\) | \(2\) | \(3\) | \(6\) | × | \(-6\) | \(-3\) | \(-2\) | \(-1\) |
※ \(x\) も \(y\) も整数となる組をとる。
対応する \(x\) と \(y\) の組を座標とする点をとり、なめらかな曲線をひくと、
※ グラフは \(x\) 軸、 \(y\) 軸と交わらない。
問題解説(3)
問題
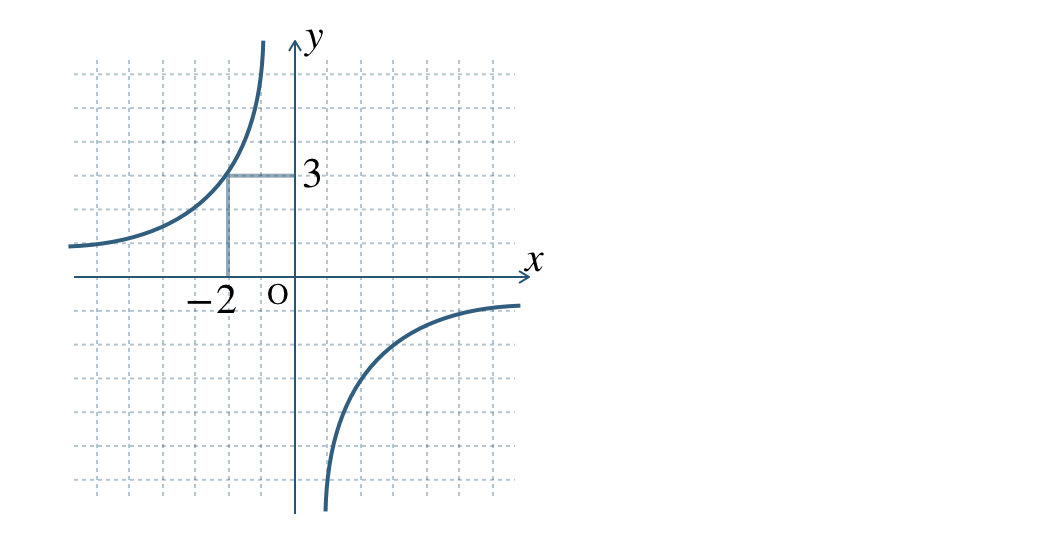
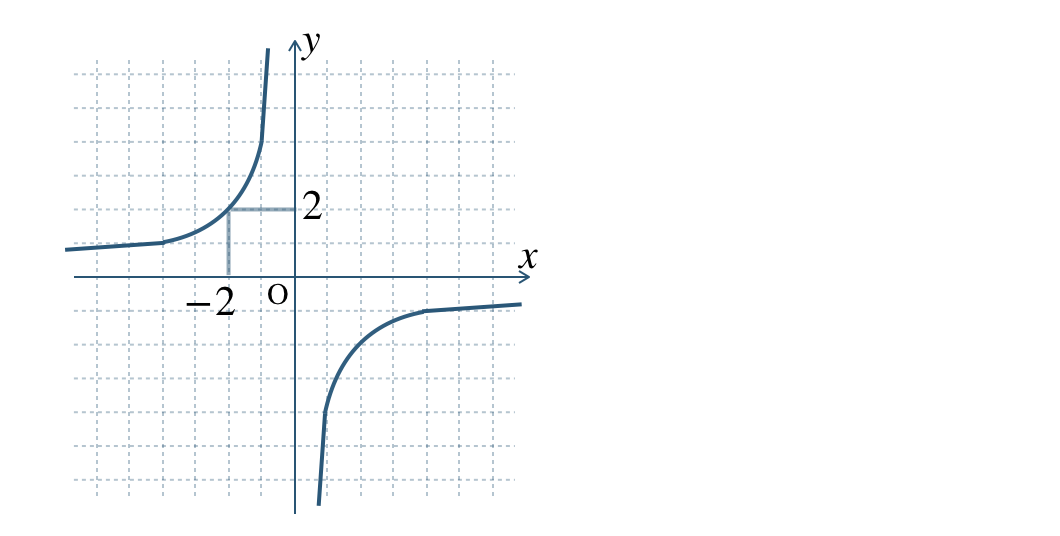
\(\begin{split}{\small (3)}~y=-\frac{\,4\,}{\,x\,}\end{split}\)
次の反比例のグラフかけ。
\(\begin{split}{\small (3)}~y=-\frac{\,4\,}{\,x\,}\end{split}\)
\(x=-4~,~-2~,~-1~,~1~,~2~,~4\) のときの \(y\) の値をまとめると、
| \(x\) | \(-4\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(4\) |
| \(y\) | \(1\) | \(2\) | \(4\) | × | \(-4\) | \(-2\) | \(-1\) |
※ \(x\) も \(y\) も整数となる組をとる。
対応する \(x\) と \(y\) の組を座標とする点をとり、なめらかな曲線をひくと、
※ グラフは \(x\) 軸、 \(y\) 軸と交わらない。

【問題一覧】中1|比例と反比例
このページは「中学数学1 比例と反比例」の問題一覧ページとなります。解説の見たい単元名がわからないと...


