問題:比例の利用
AさんとBさんが \(800~{\rm m}\) を走った。スタートしてからの時間 \(x\) 分で走った道のり \(y~{\rm m}\) としたとき、AさんとBさんの \(x\) と \(y\) の関係をグラフで表すと下のようになった。
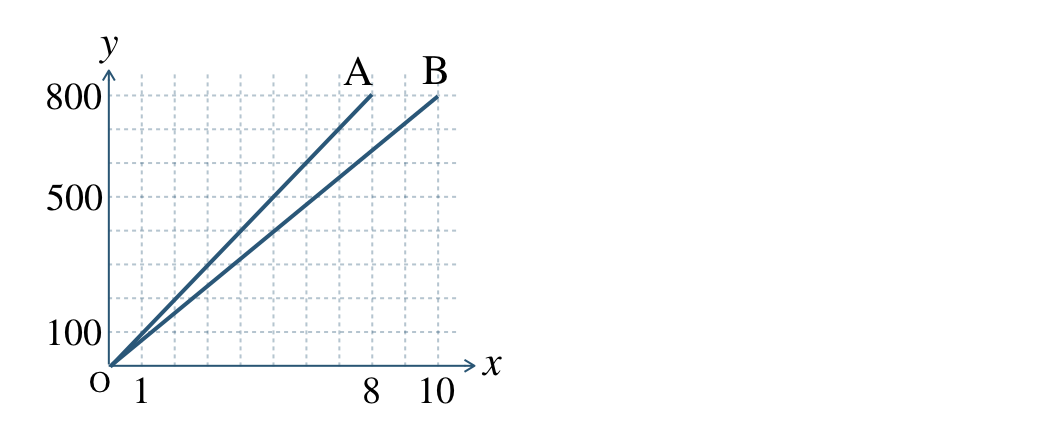
次の問いに答えよ。
\({\small (1)}~\)AさんとBさんはそれぞれ分速何 \({\rm m}\) で走ったか答えよ。
\({\small (2)}~\)AさんとBさんそれぞれの \(x\) と \(y\) の関係を式で表し、\(x\) の変域も答えよ。
\({\small (3)}~\)スタートして \(5\) 分後の2人の差は何 \({\rm m}\) か答えよ。
解法のPoint
スタートして \(x\) 分後の道のりを \(y~{\rm m}\) としたとき、\(y\) と \(x\) の関係をグラフは、

このとき、\(y\) を \(x\) の式で表すと、\(\begin{split}y=50x\end{split}\)
比例定数 \(50\) が速さと等しくなるので、
速さは、分速 \(50~{\rm m}\)
また、\(300~{\rm m}\) までに \(6\) 分かかるので、
\(x\) の変域は、\(0≦x≦6\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:比例の利用
問題解説(1)
AさんとBさんが \(800~{\rm m}\) を走った。スタートしてからの時間 \(x\) 分で走った道のり \(y~{\rm m}\) としたとき、AさんとBさんの \(x\) と \(y\) の関係をグラフで表すと下のようになった。

次の問いに答えよ。
\({\small (1)}~\)AさんとBさんはそれぞれ分速何 \({\rm m}\) で走ったか答えよ。
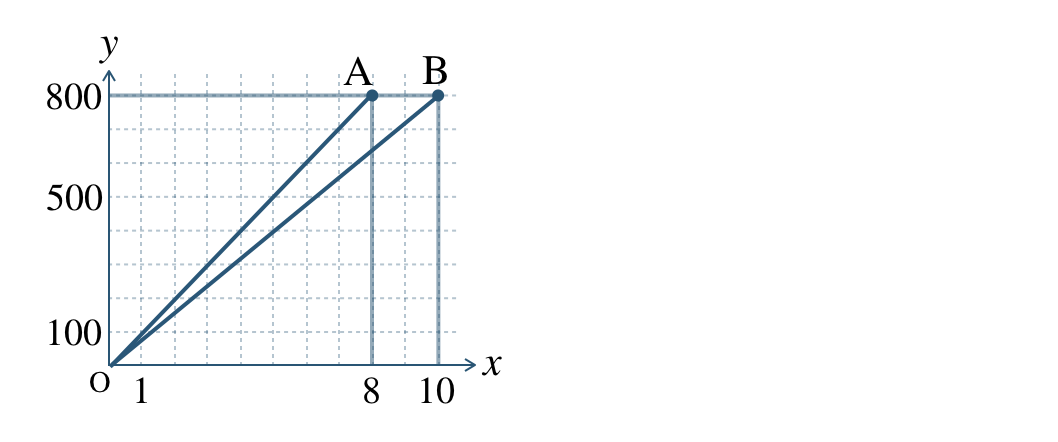
Aさんはスタートして \(8\) 分後に \(800~{\rm m}\) 走っているので、速さ=道のり÷時間より、
\(\begin{split}~~~800{\, \small \div \,}8=100\end{split}\)
Bさんはスタートして \(10\) 分後に \(800~{\rm m}\) 走っているので、速さ=道のり÷時間より、
\(\begin{split}~~~800{\, \small \div \,}10=80\end{split}\)
したがって、
Aさん 分速 \(100~{\rm m}\)
Bさん 分速 \(80~{\rm m}\)
となる
問題解説(2)
AさんとBさんが \(800~{\rm m}\) を走った。スタートしてからの時間 \(x\) 分で走った道のり \(y~{\rm m}\) としたとき、AさんとBさんの \(x\) と \(y\) の関係をグラフで表すと下のようになった。

次の問いに答えよ。
\({\small (2)}~\)AさんとBさんそれぞれの \(x\) と \(y\) の関係を式で表し、\(x\) の変域も答えよ。
Aさんは分速 \(100~{\rm m}\) で走るので、比例定数が \(100\) となり、\(x\) と \(y\) の関係を式は、
\(\begin{split}~~~y=100x\end{split}\)
また、グラフより \(8\) 分後に着くので、\(x\) の変域は、
\(\begin{split}~~~0≦x≦8\end{split}\)
となる
Bさんは分速 \(80~{\rm m}\) で走るので、比例定数が \(80\) となり、\(x\) と \(y\) の関係を式は、
\(\begin{split}~~~y=80x\end{split}\)
また、グラフより \(10\) 分後に着くので、\(x\) の変域は、
\(\begin{split}~~~0≦x≦10\end{split}\)
となる
したがって、
Aさん \(y=100x~~(0≦x≦8)\)
Bさん \(y=80x~~(0≦x≦10)\)
となる
問題解説(3)
AさんとBさんが \(800~{\rm m}\) を走った。スタートしてからの時間 \(x\) 分で走った道のり \(y~{\rm m}\) としたとき、AさんとBさんの \(x\) と \(y\) の関係をグラフで表すと下のようになった。

次の問いに答えよ。
\({\small (3)}~\)スタートして \(5\) 分後の2人の差は何 \({\rm m}\) か答えよ。
\(5\) 分後の2人の走った道のりは、
Aさんは、\(y=100x\) に \(x=5\) を代入すると、
\(\begin{split}~~~y=100{\, \small \times \,}5=500\end{split}\)
Bさんは、\(y=80x\) に \(x=5\) を代入すると、
\(\begin{split}~~~y=80{\, \small \times \,}5=400\end{split}\)
よって、2人の道のりの差は、
\(\begin{split}~~~500-400=100\end{split}\)
したがって、2人の差は \(100~{\rm m}\) となる
【別解】 グラフで考えると、
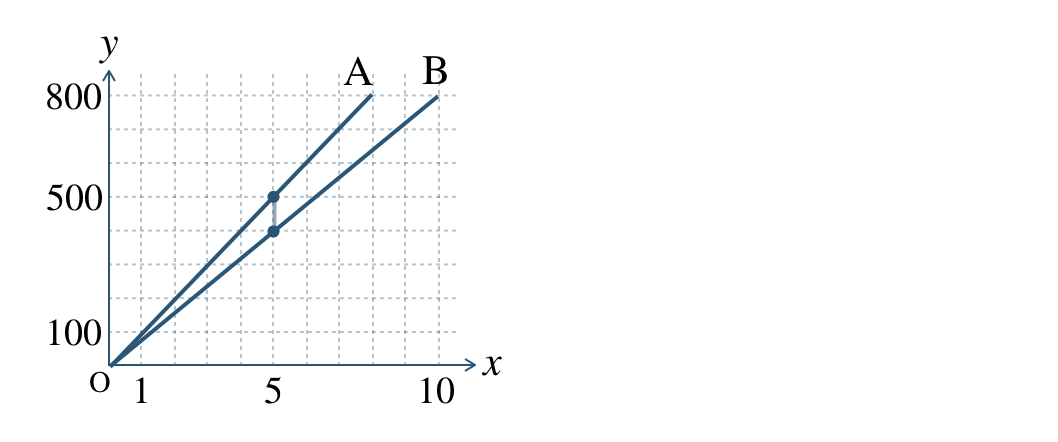
\(5\) 分後のときの2本の直線の差より、\(100~{\rm m}\) となる



