問題:円とおうぎ形の計量
問題
\({\small (1)}~\)半径 \(3~{\rm cm}\) の円について、次のものを求めよ。
① 円周の長さ \({\rm cm}\)
② 円の面積 \({\rm cm}^2\)
\({\small (2)}~\)半径 \(4~{\rm cm}\)、中心角 \(45^\circ\) のおうぎ形について、次のものを求めよ。
① 弧の長さ \({\rm cm}\)
② おうぎ形の面積 \({\rm cm}^2\)
\({\small (3)}~\)半径 \(6~{\rm cm}\)、中心角 \(120^\circ\) のおうぎ形について、次のものを求めよ。
① 弧の長さ \({\rm cm}\)
② おうぎ形の面積 \({\rm cm}^2\)
\({\small (4)}~\)半径 \(8~{\rm cm}\)、弧の長さ \(4\pi~{\rm cm}\) のおうぎ形について、次のものを求めよ。
① 中心角の大きさ
② おうぎ形の面積 \({\rm cm}^2\)
次の問いに答えよ。
\({\small (1)}~\)半径 \(3~{\rm cm}\) の円について、次のものを求めよ。
① 円周の長さ \({\rm cm}\)
② 円の面積 \({\rm cm}^2\)
\({\small (2)}~\)半径 \(4~{\rm cm}\)、中心角 \(45^\circ\) のおうぎ形について、次のものを求めよ。
① 弧の長さ \({\rm cm}\)
② おうぎ形の面積 \({\rm cm}^2\)
\({\small (3)}~\)半径 \(6~{\rm cm}\)、中心角 \(120^\circ\) のおうぎ形について、次のものを求めよ。
① 弧の長さ \({\rm cm}\)
② おうぎ形の面積 \({\rm cm}^2\)
\({\small (4)}~\)半径 \(8~{\rm cm}\)、弧の長さ \(4\pi~{\rm cm}\) のおうぎ形について、次のものを求めよ。
① 中心角の大きさ
② おうぎ形の面積 \({\rm cm}^2\)
解法のPoint
Point:円の周の長さと面積

\(\begin{split}l=2\pi r\end{split}\)
円の面積 \(S\) は、半径×半径×円周率より、
\(\begin{split}S=\pi r^2\end{split}\)
円の周の長さと面積は、

半径 \(r\) の円の周の長さ \(l\) は、直径×円周率より、
\(\begin{split}l=2\pi r\end{split}\)
円の面積 \(S\) は、半径×半径×円周率より、
\(\begin{split}S=\pi r^2\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:おうぎ形の弧の長さと面積
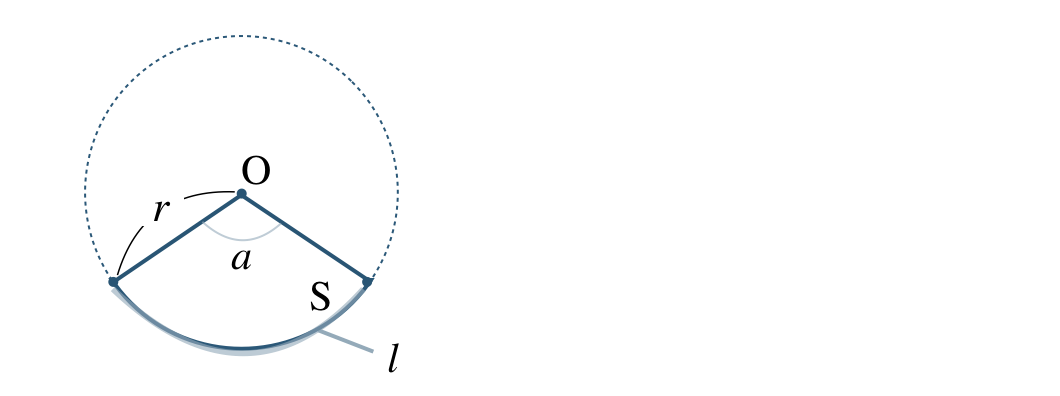
\(\begin{split}l=2\pi r{\, \small \times \,}\frac{\,a\,}{\,360\,}\end{split}\)
おうぎ形の面積 \(S\) は、円の面積の \(\begin{split}{ \frac{\,a\,}{\,360\,}}\end{split}\) 倍
\(\begin{split}S=\pi r^2{\, \small \times \,}\frac{\,a\,}{\,360\,}\end{split}\)
1つの円からできるおうぎ形(半径の等しいおうぎ形)について、弧の長さや面積はその中心角の大きさで決まる。
また、1つの円ではおうぎ形の弧の長さや面積は中心角に比例する。

弧の長さ \(l\) は、円周の長さの \(\begin{split}{ \frac{\,a\,}{\,360\,}}\end{split}\) 倍
\(\begin{split}l=2\pi r{\, \small \times \,}\frac{\,a\,}{\,360\,}\end{split}\)
おうぎ形の面積 \(S\) は、円の面積の \(\begin{split}{ \frac{\,a\,}{\,360\,}}\end{split}\) 倍
\(\begin{split}S=\pi r^2{\, \small \times \,}\frac{\,a\,}{\,360\,}\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:弧の長さから中心角の求め方
同じ半径 \(6~{\rm cm}\) の円の円周の長さは、
\(\begin{split}2{\, \small \times \,}6{\, \small \times \,}\pi=12\pi\end{split}\)
中心角を \(a\) とすると、弧の長さが \(4\pi\) は円周の長さの \(\begin{split}{ \frac{\,a\,}{\,360\,}}\end{split}\) 倍となるので、
\(\begin{eqnarray}~12\pi{\, \small \times \,}\frac{\,a\,}{\,360\,}&=&4\pi
\\[3pt]~~~a&=&120
\end{eqnarray}\)
よって、中心角は \(120^\circ\) となる
また、おうぎ形の面積は、
\(\begin{split}6{\, \small \times \,}6{\, \small \times \,}\pi{\, \small \times \,}\frac{\,120\,}{\,360\,}=12\pi~{\rm cm^2}\end{split}\)
半径 \(6~{\rm cm}\) のおうぎ形の弧の長さが \(4\pi~{\rm cm}\) のときの中心角と面積は、
同じ半径 \(6~{\rm cm}\) の円の円周の長さは、
\(\begin{split}2{\, \small \times \,}6{\, \small \times \,}\pi=12\pi\end{split}\)
中心角を \(a\) とすると、弧の長さが \(4\pi\) は円周の長さの \(\begin{split}{ \frac{\,a\,}{\,360\,}}\end{split}\) 倍となるので、
\(\begin{eqnarray}~12\pi{\, \small \times \,}\frac{\,a\,}{\,360\,}&=&4\pi
\\[3pt]~~~a&=&120
\end{eqnarray}\)
よって、中心角は \(120^\circ\) となる
また、おうぎ形の面積は、
\(\begin{split}6{\, \small \times \,}6{\, \small \times \,}\pi{\, \small \times \,}\frac{\,120\,}{\,360\,}=12\pi~{\rm cm^2}\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:円とおうぎ形の計量
問題解説(1)
問題
\({\small (1)}~\)半径 \(3~{\rm cm}\) の円について、次のものを求めよ。
① 円周の長さ \({\rm cm}\)
② 円の面積 \({\rm cm}^2\)
次の問いに答えよ。
\({\small (1)}~\)半径 \(3~{\rm cm}\) の円について、次のものを求めよ。
① 円周の長さ \({\rm cm}\)
② 円の面積 \({\rm cm}^2\)

① 円周の長さは、直径×円周率より、
\(\begin{split}~~~2{\, \small \times \,}3{\, \small \times \,}\pi=6\pi~{\rm cm}\end{split}\)
したがって、\(6\pi~{\rm cm}\) となる
② 円の面積は、半径×半径×円周率より、
\(\begin{split}~~~3{\, \small \times \,}3{\, \small \times \,}\pi=9\pi~{\rm cm}^2\end{split}\)
したがって、\(9\pi~{\rm cm}^2\) となる
問題解説(2)
問題
\({\small (2)}~\)半径 \(4~{\rm cm}\)、中心角 \(45^\circ\) のおうぎ形について、次のものを求めよ。
① 弧の長さ \({\rm cm}\)
② おうぎ形の面積 \({\rm cm}^2\)
次の問いに答えよ。
\({\small (2)}~\)半径 \(4~{\rm cm}\)、中心角 \(45^\circ\) のおうぎ形について、次のものを求めよ。
① 弧の長さ \({\rm cm}\)
② おうぎ形の面積 \({\rm cm}^2\)
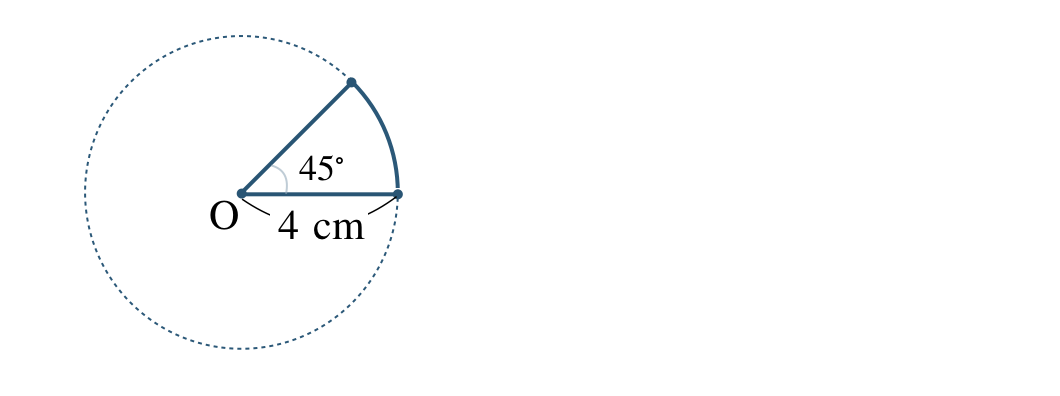
① 同じ半径の円の円周の長さの \(\begin{split}{\frac{\,45\,}{\,360\,}}\end{split}\) 倍となるので、
\(\begin{split}\require{cancel} \begin{split}&2{\, \small \times \,} 4{\, \small \times \,} \pi {\, \small \times \,}\frac{\,45\,}{\,360\,}\\[3pt]~~=~&8\pi {\, \small \times \,} \frac{\,\cancel{45}^{1}\,}{\,\cancel{360}^{8}\,}\\[3pt]~~=~&8\pi {\, \small \times \,}\frac{\,1\,}{\,8\,}\\[3pt]~~=~&\pi\end{split}\end{split}\)
したがって、\(\pi~{\rm cm}\) となる
② 同じ半径の円の面積の \(\begin{split}{\frac{\,45\,}{\,360\,}}\end{split}\) 倍となるので、
\(\begin{split}\require{cancel} \begin{split}&4{\, \small \times \,} 4{\, \small \times \,} \pi {\, \small \times \,}\frac{\,45\,}{\,360\,}\\[3pt]~~=~&16\pi {\, \small \times \,} \frac{\,\cancel{45}^{1}\,}{\,\cancel{360}^{8}\,}\\[3pt]~~=~&16\pi {\, \small \times \,}\frac{\,1\,}{\,8\,}\\[3pt]~~=~&2\pi\end{split}\end{split}\)
したがって、\(2\pi~{\rm cm}^2\) となる
問題解説(3)
問題
\({\small (3)}~\)半径 \(6~{\rm cm}\)、中心角 \(120^\circ\) のおうぎ形について、次のものを求めよ。
① 弧の長さ \({\rm cm}\)
② おうぎ形の面積 \({\rm cm}^2\)
次の問いに答えよ。
\({\small (3)}~\)半径 \(6~{\rm cm}\)、中心角 \(120^\circ\) のおうぎ形について、次のものを求めよ。
① 弧の長さ \({\rm cm}\)
② おうぎ形の面積 \({\rm cm}^2\)
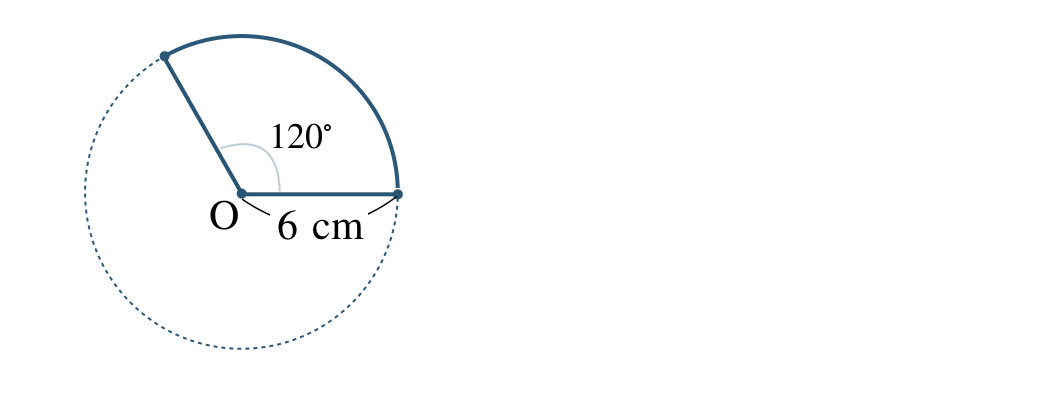
① 同じ半径の円の円周の長さの \(\begin{split}{\frac{\,120\,}{\,360\,}}\end{split}\) 倍となるので、
\(\begin{split}\require{cancel} \begin{split}&2{\, \small \times \,} 6{\, \small \times \,} \pi {\, \small \times \,}\frac{\,120\,}{\,360\,}\\[3pt]~~=~&12\pi {\, \small \times \,} \frac{\,\cancel{120}^{1}\,}{\,\cancel{360}^{3}\,}\\[3pt]~~=~&12\pi {\, \small \times \,}\frac{\,1\,}{\,3\,}\\[3pt]~~=~&4\pi\end{split}\end{split}\)
したがって、\(4\pi~{\rm cm}\) となる
② 同じ半径の円の面積の \(\begin{split}{\frac{\,120\,}{\,360\,}}\end{split}\) 倍となるので、
\(\begin{split}\require{cancel} \begin{split}&6{\, \small \times \,} 6{\, \small \times \,} \pi {\, \small \times \,}\frac{\,120\,}{\,360\,}\\[3pt]~~=~&36\pi {\, \small \times \,} \frac{\,\cancel{120}^{1}\,}{\,\cancel{360}^{3}\,}\\[3pt]~~=~&36\pi {\, \small \times \,}\frac{\,1\,}{\,3\,}\\[3pt]~~=~&12\pi\end{split}\end{split}\)
したがって、\(12\pi~{\rm cm}^2\) となる
問題解説(4)
問題
\({\small (4)}~\)半径 \(8~{\rm cm}\)、弧の長さ \(4\pi~{\rm cm}\) のおうぎ形について、次のものを求めよ。
① 中心角の大きさ
② おうぎ形の面積 \({\rm cm}^2\)
次の問いに答えよ。
\({\small (4)}~\)半径 \(8~{\rm cm}\)、弧の長さ \(4\pi~{\rm cm}\) のおうぎ形について、次のものを求めよ。
① 中心角の大きさ
② おうぎ形の面積 \({\rm cm}^2\)
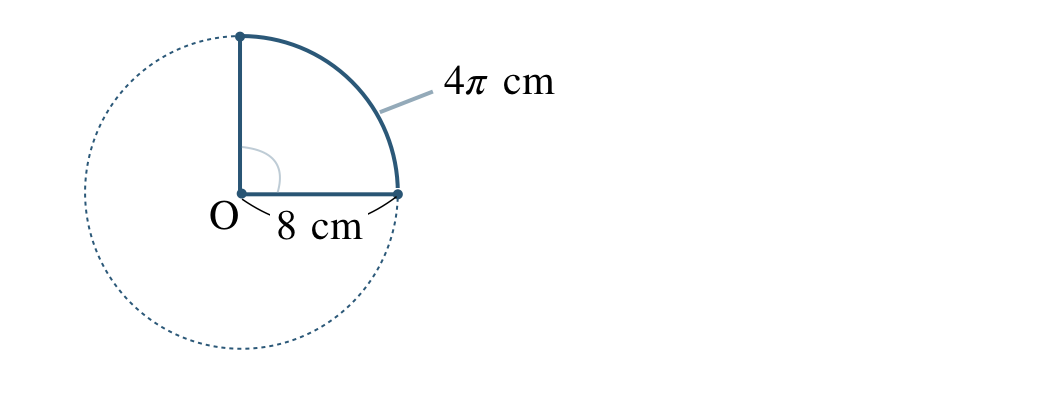
① 同じ半径の円の円周の長さは、
\(\begin{split}~~~2{\, \small \times \,}8{\, \small \times \,} \pi=16\pi~{\rm cm}\end{split}\)
このおうぎ形の中心角を \(a^\circ\) とすると、
弧の長さ \(4\pi~{\rm cm}\) は同じ半径の円の円周の長さの \(\begin{split}{\frac{\,a\,}{\,360\,}}\end{split}\) 倍となるので、
\(\begin{eqnarray}~~~16\pi {\, \small \times \,}\frac{\,a\,}{\,360\,}&=&4\pi\\[3pt]~~~16\pi {\, \small \times \,}\frac{\,a\,}{\,360\,}{\, \small \times \,}\frac{\,360\,}{\,16\pi\,}&=&4\pi {\, \small \times \,} \frac{\,360\,}{\,16\pi\,}\\[3pt]~~~a&=&\frac{\,360\,}{\,4\,}\\[3pt]~~~a&=&90\end{eqnarray}\)
したがって、中心角 \(90^\circ\) となる
② 同じ半径の円の面積の \(\begin{split}{\frac{\,90\,}{\,360\,}}\end{split}\) 倍となるので、
\(\begin{split}\require{cancel} \begin{split}&8{\, \small \times \,} 8{\, \small \times \,} \pi {\, \small \times \,}\frac{\,90\,}{\,360\,}\\[3pt]~~=~&64\pi {\, \small \times \,} \frac{\,\cancel{90}^{1}\,}{\,\cancel{360}^{4}\,}\\[3pt]~~=~&64\pi {\, \small \times \,}\frac{\,1\,}{\,4\,}\\[3pt]~~=~&16\pi\end{split}\end{split}\)
したがって、\(16\pi~{\rm cm}^2\) となる

【問題一覧】中1|平面図形
このページは「中学数学1 平面図形」の問題一覧ページとなります。解説の見たい単元名がわからないときは...


