問題:平面の回転体
問題
\({\small (1)}~\)次の図を直線 \(l\) で回転させてできる立体の見取り図をかけ。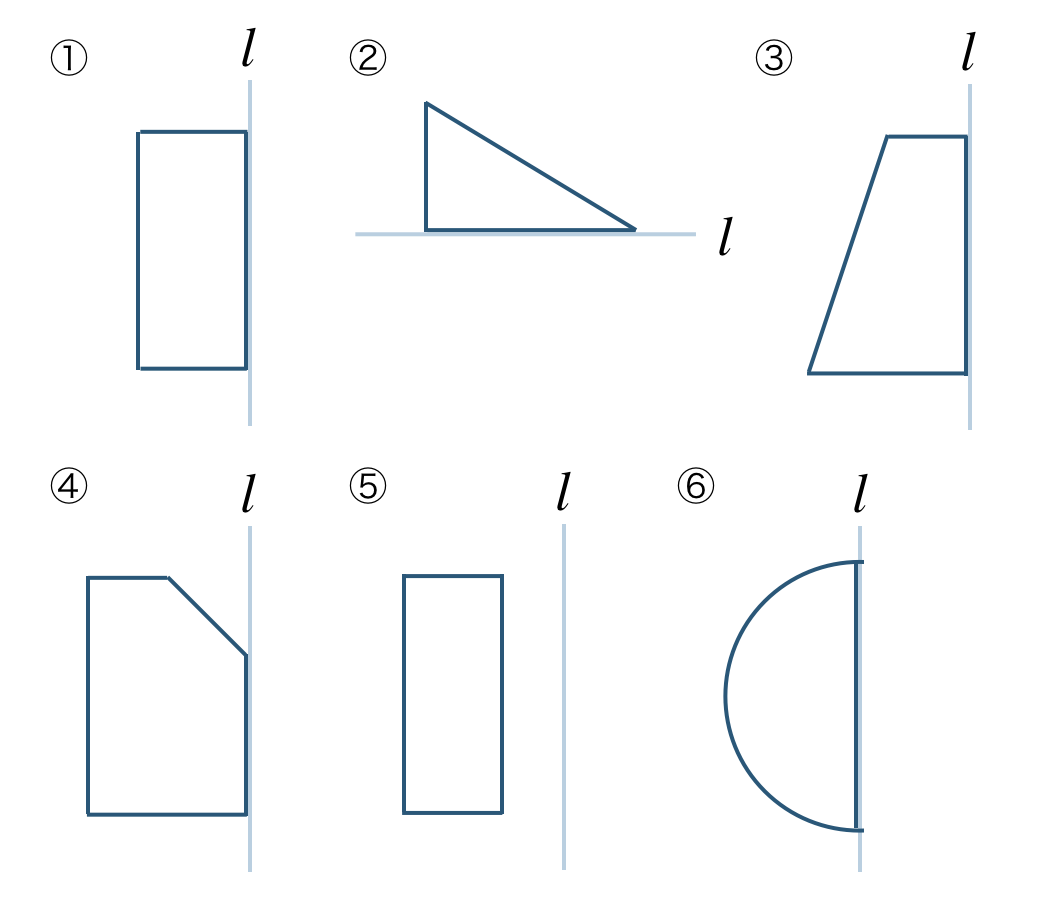
次の問いに答えよ。
\({\small (1)}~\)次の図を直線 \(l\) で回転させてできる立体の見取り図をかけ。
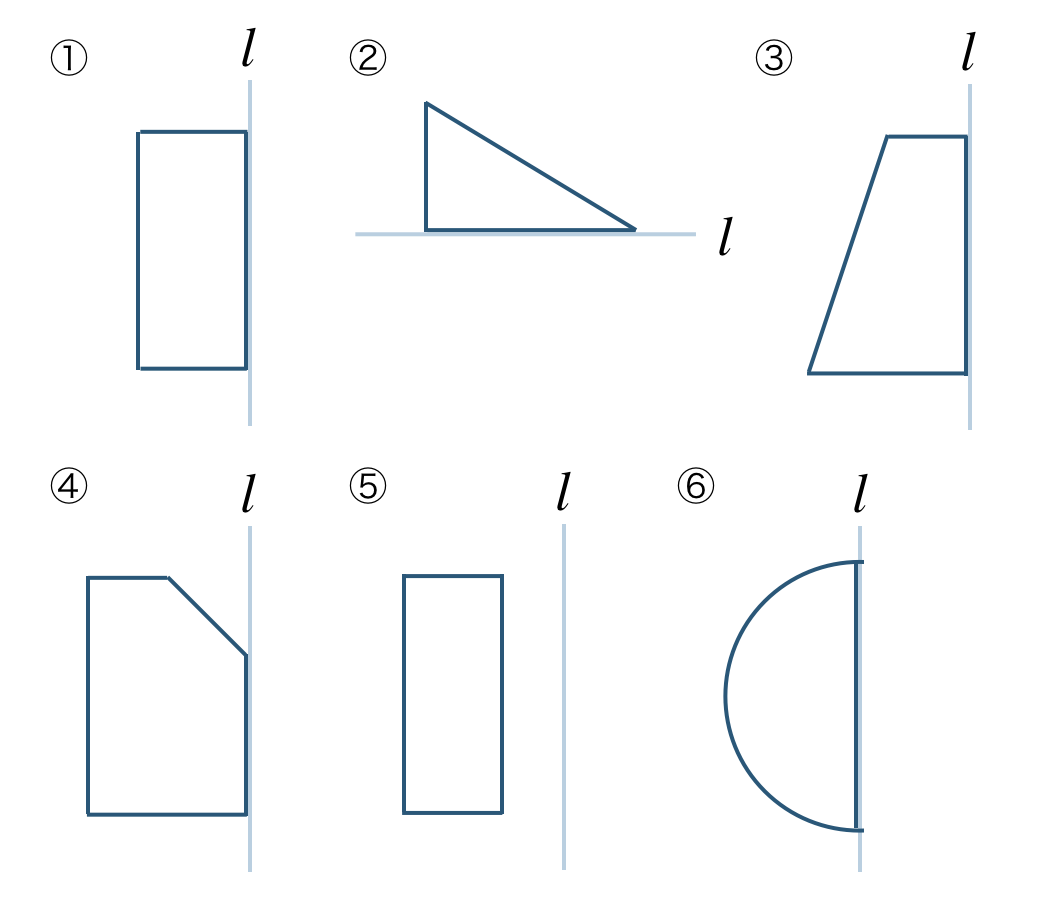
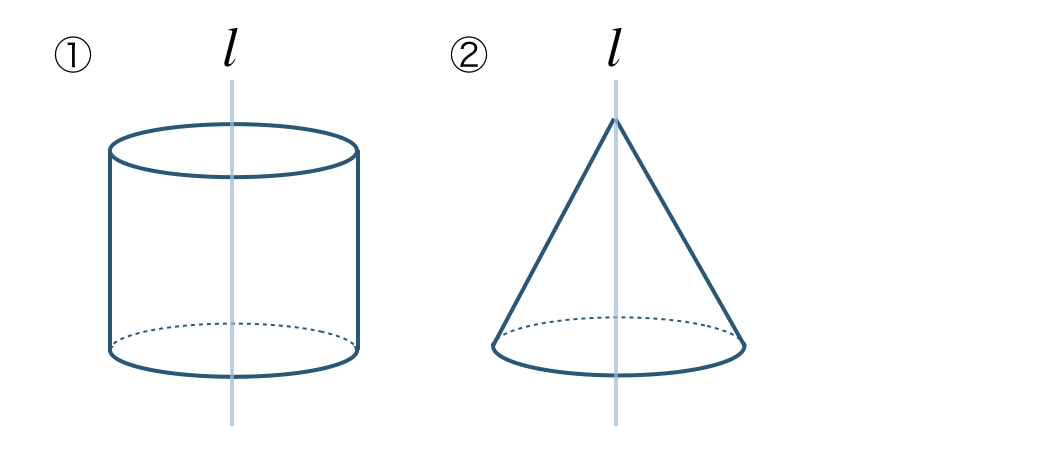
\({\small (2)}~\)次の立体を回転の軸をふくむ平面と、回転の軸に垂直な平面で切った切り口はそれぞれどな図形となるか答えよ。

解法のPoint
Point:平面の回転体
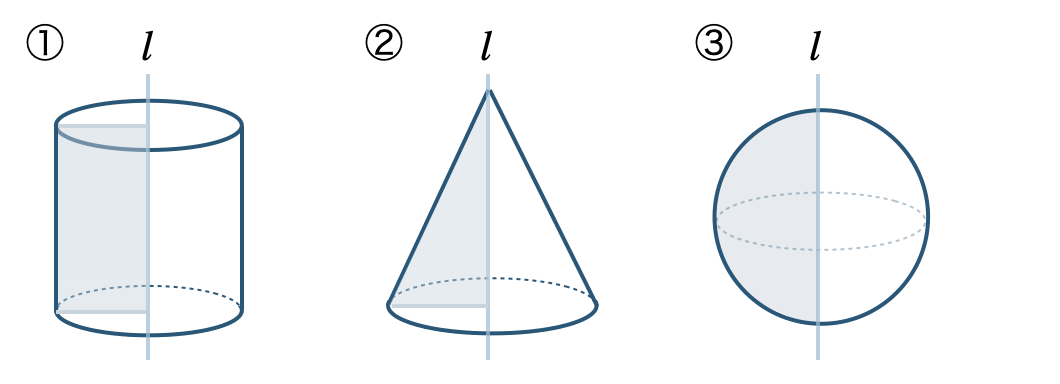
また、円柱や円錐の側面をえがく線分を、円柱や円錐の「母線」という。
ある直線 \(l\) を軸として、平面図形を1回転させてできる立体を「回転体」という。

① 長方形を回転させると、円柱となる
② 直角三角形を回転させると、円錐となる
③ 半円を回転させると、球となる
また、円柱や円錐の側面をえがく線分を、円柱や円錐の「母線」という。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:平面の回転体
問題解説(1)
問題
\({\small (1)}~\)次の図を直線 \(l\) で回転させてできる立体の見取り図をかけ。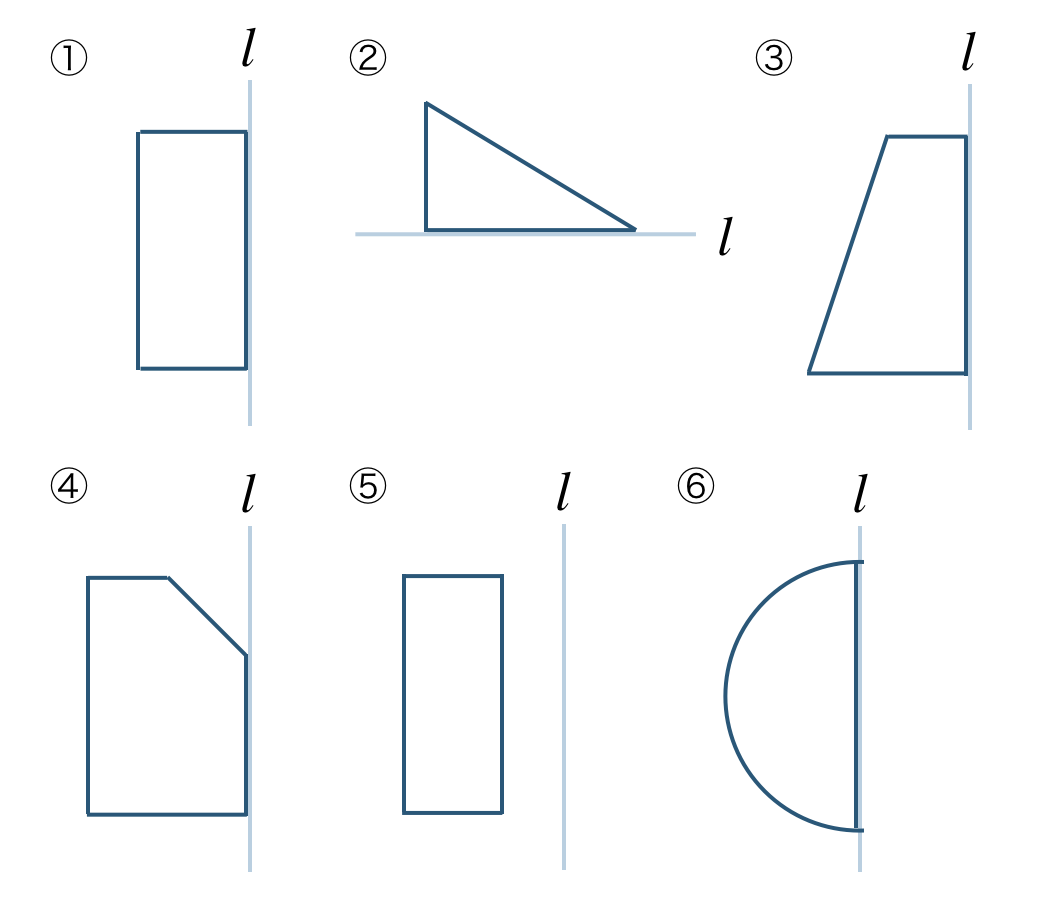
次の問いに答えよ。
\({\small (1)}~\)次の図を直線 \(l\) で回転させてできる立体の見取り図をかけ。
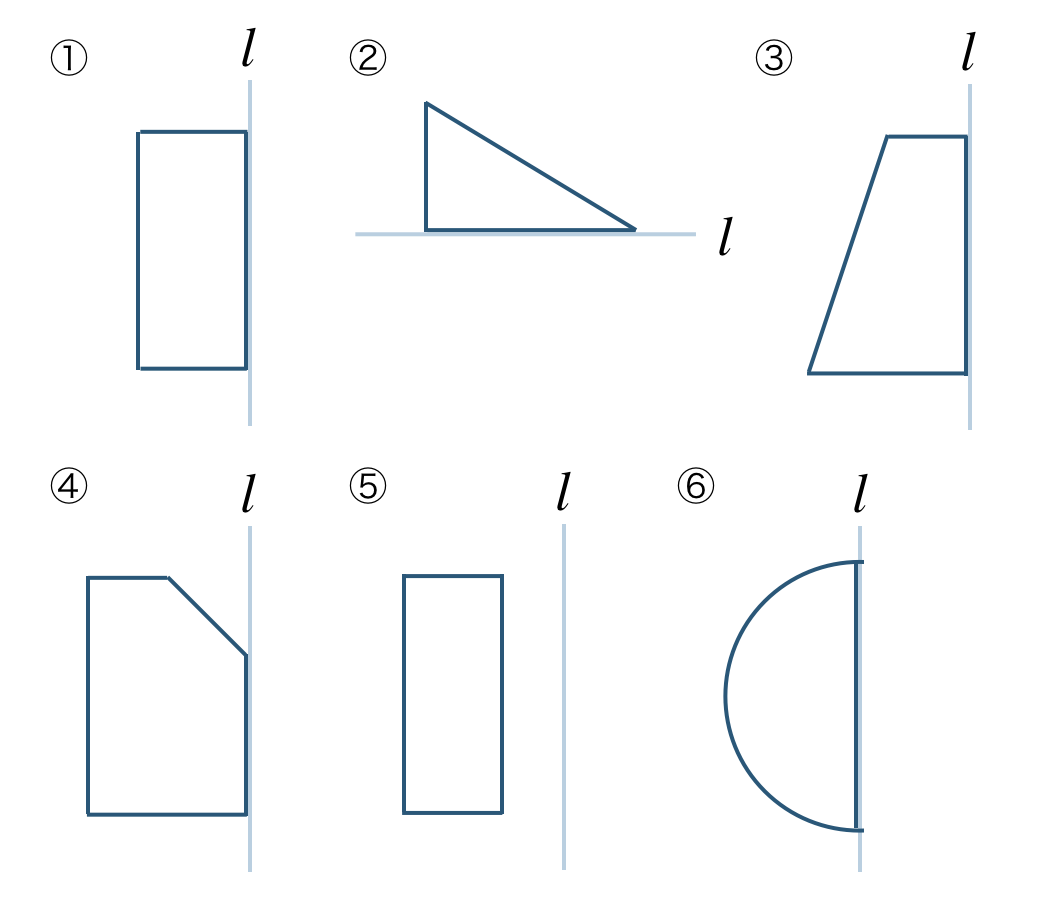
① 直線 \(l\) を軸として、線対称した図形をかくと、

頂点 \({\rm A~,~B}\) が直線 \(l\) を軸として回転した円をかくと回転体となる
② 直線 \(l\) を軸として、線対称した図形をかくと、

頂点 \({\rm A}\) が直線 \(l\) を軸として回転した円をかくと回転体となる

③ 直線 \(l\) を軸として、線対称した図形をかくと、

頂点 \({\rm A~,~B}\) が直線 \(l\) を軸として回転した円をかくと回転体となる
④ 直線 \(l\) を軸として、線対称した図形をかくと、

頂点 \({\rm A~,~B~,~C}\) が直線 \(l\) を軸として回転した円をかくと回転体となる
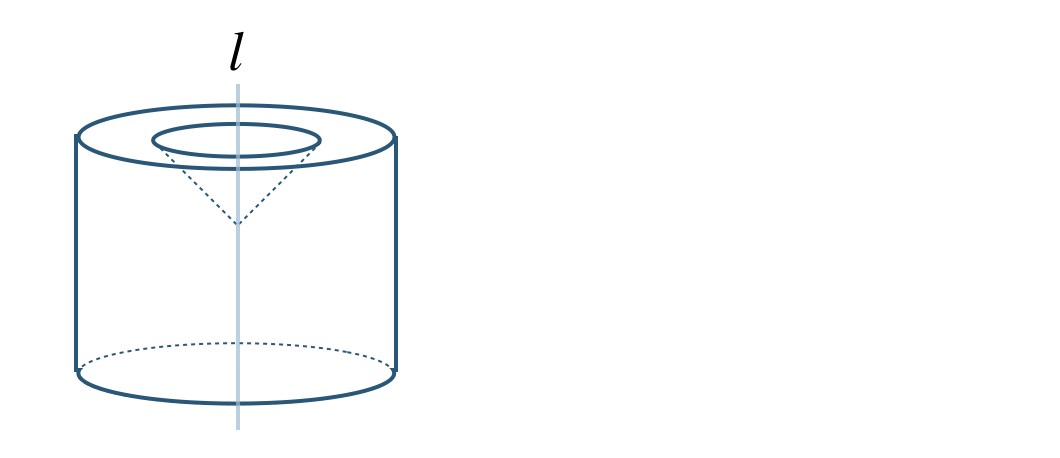
⑤ 直線 \(l\) を軸として、線対称した図形をかくと、

頂点 \({\rm A~,~B~,~C~,~D}\) が直線 \(l\) を軸として回転した円をかくと回転体となる
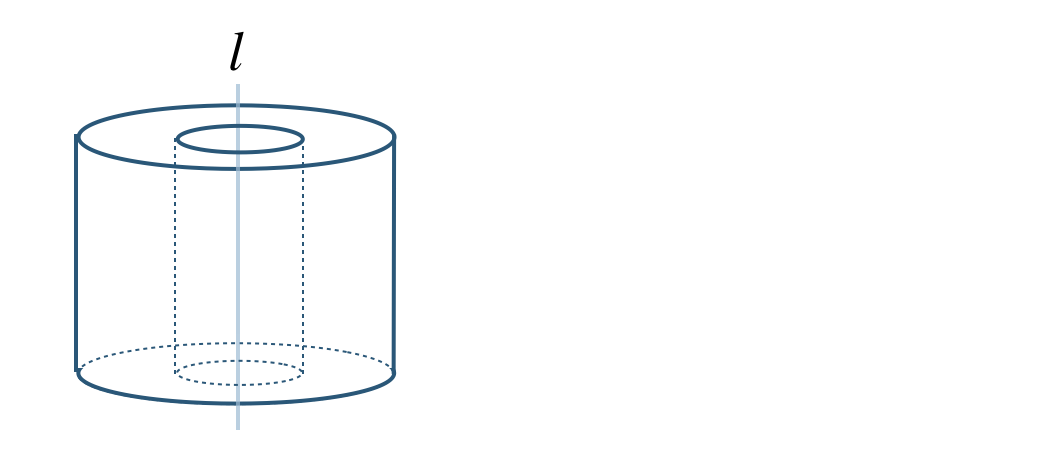
⑥ 直線 \(l\) を軸として、線対称した図形をかくと、

弧を回転させると球となる

問題解説(2)
問題
\({\small (2)}~\)次の立体を回転の軸をふくむ平面と、回転の軸に垂直な平面で切った切り口はそれぞれどな図形となるか答えよ。
次の問いに答えよ。
\({\small (2)}~\)次の立体を回転の軸をふくむ平面と、回転の軸に垂直な平面で切った切り口はそれぞれどな図形となるか答えよ。

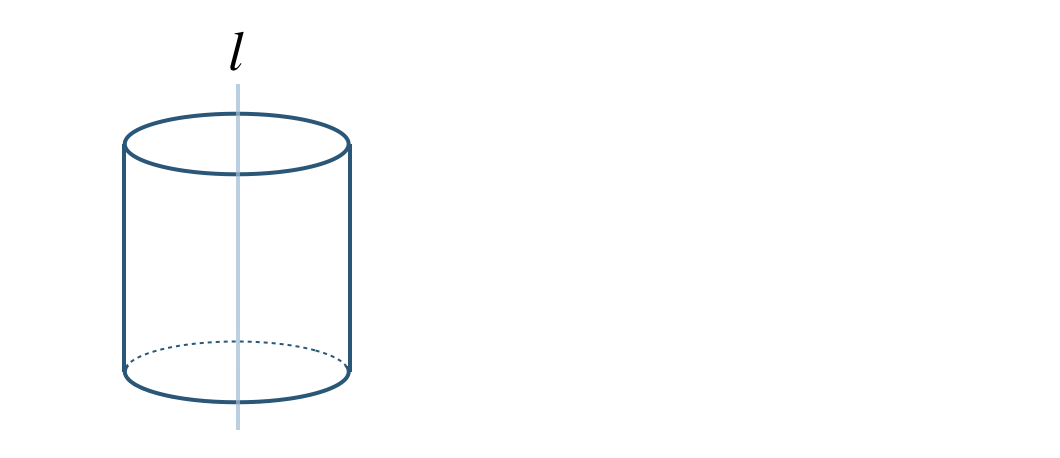
① 回転の軸をふくむ平面で切ると、
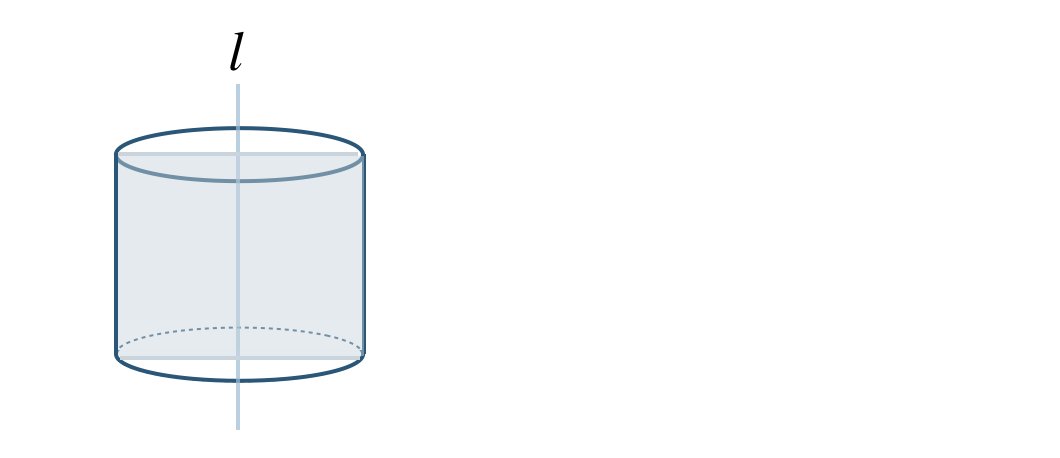
これより、長方形 となる
回転の軸に垂直な平面で切ると、
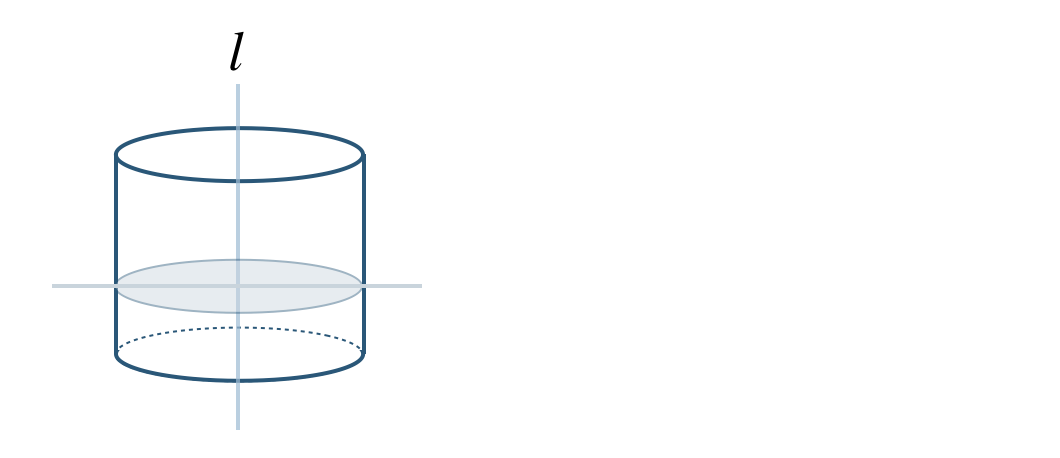
これより、円 となる
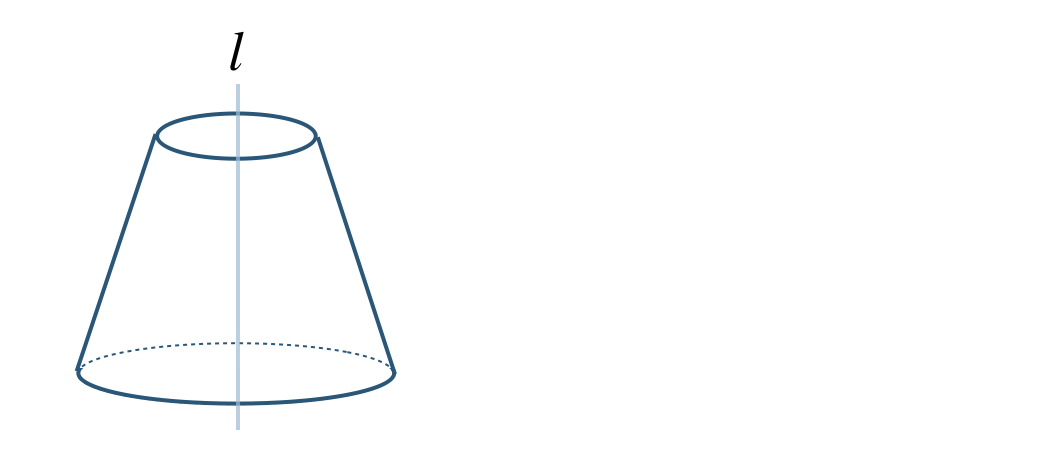
② 回転の軸をふくむ平面で切ると、

これより、三角形 となる
回転の軸に垂直な平面で切ると、
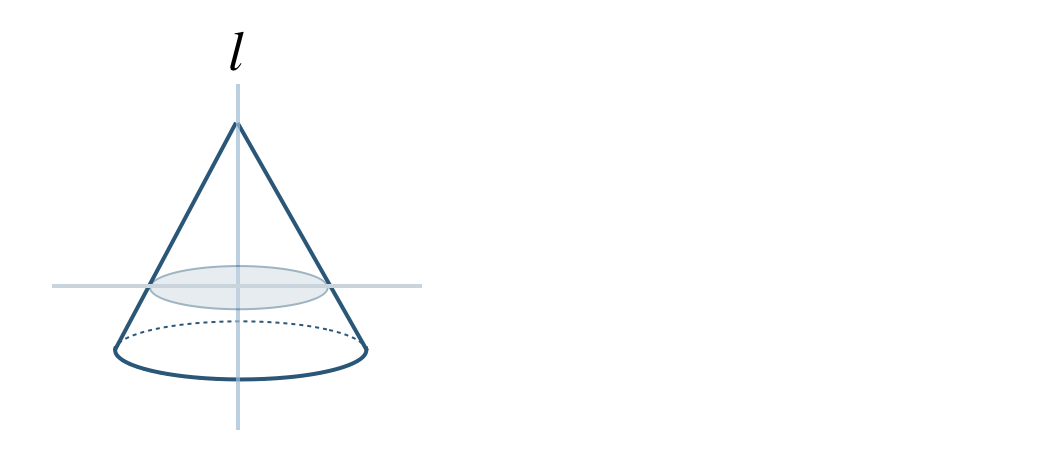
これより、円 となる

【問題一覧】中1|空間図形
このページは「中学数学1 空間図形」の問題一覧ページとなります。解説の見たい単元名がわからないときは...


