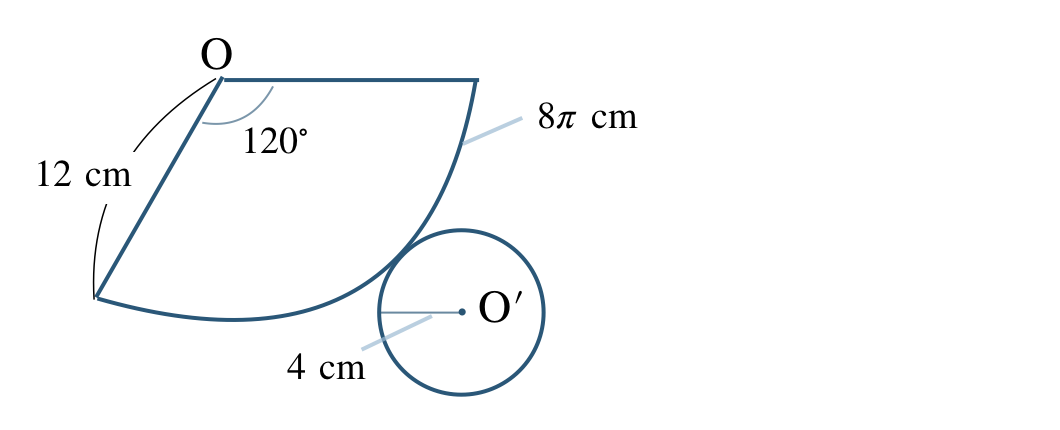立体の展開図の解法
立体を平面で表すとき、「展開図」で表す。
このとき、展開図で重なり合う線分の長さは等しい。
■ 角柱の展開図
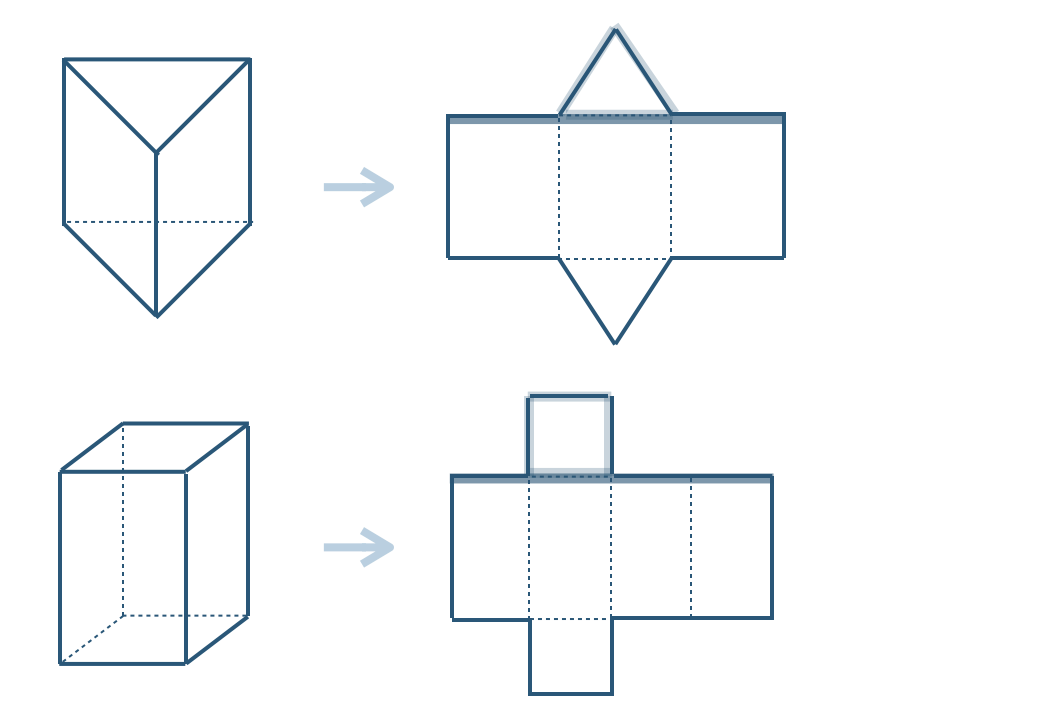
(側面の長方形の横の長さ)＝(底面の周りの長さ)
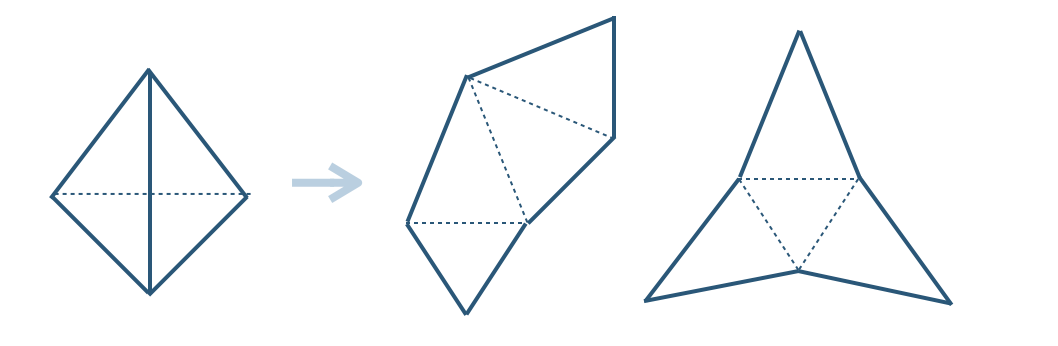
■ 角錐の展開図
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
■ 円柱 ※ 側面が長方形で底面が円となる。
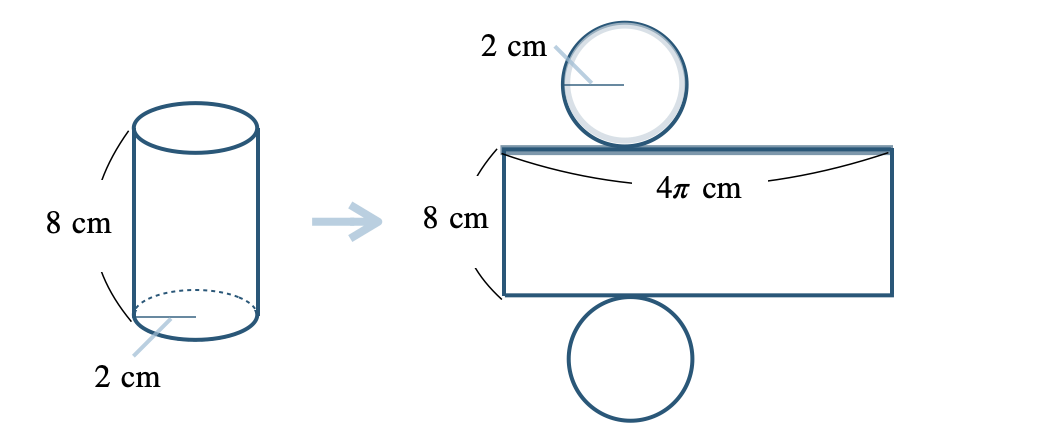
(側面の長方形の横の長さ)＝(底面の円周の長さ)
■ 円錐 ※ 側面がひし形で底面が円となる。
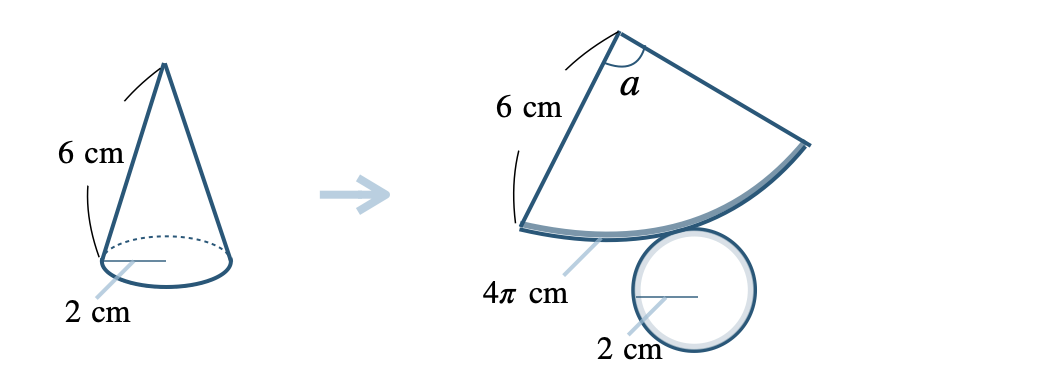
ひし形の弧の長さは、底面の円周の長さ \begin{split}4\pi~{\rm cm}\end{split}
このおうぎ形の半径は母線の 6~{\rm cm} であり、
同じ半径 6~{\rm cm} の円の円周の長さは、\begin{split}12\pi~{\rm cm}\end{split}
中心角を a とすると、弧の長さが 4\pi は円周の長さの \begin{split}{ \frac{\,a\,}{\,360\,}}\end{split} 倍となるので、
\begin{eqnarray}~12\pi{\, \small \times \,}\frac{\,a\,}{\,360\,}&=&4\pi\end{eqnarray}
よって、中心角は 120^\circ となる
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説：立体の展開図
問題解説(1)
次の問いに答えよ。
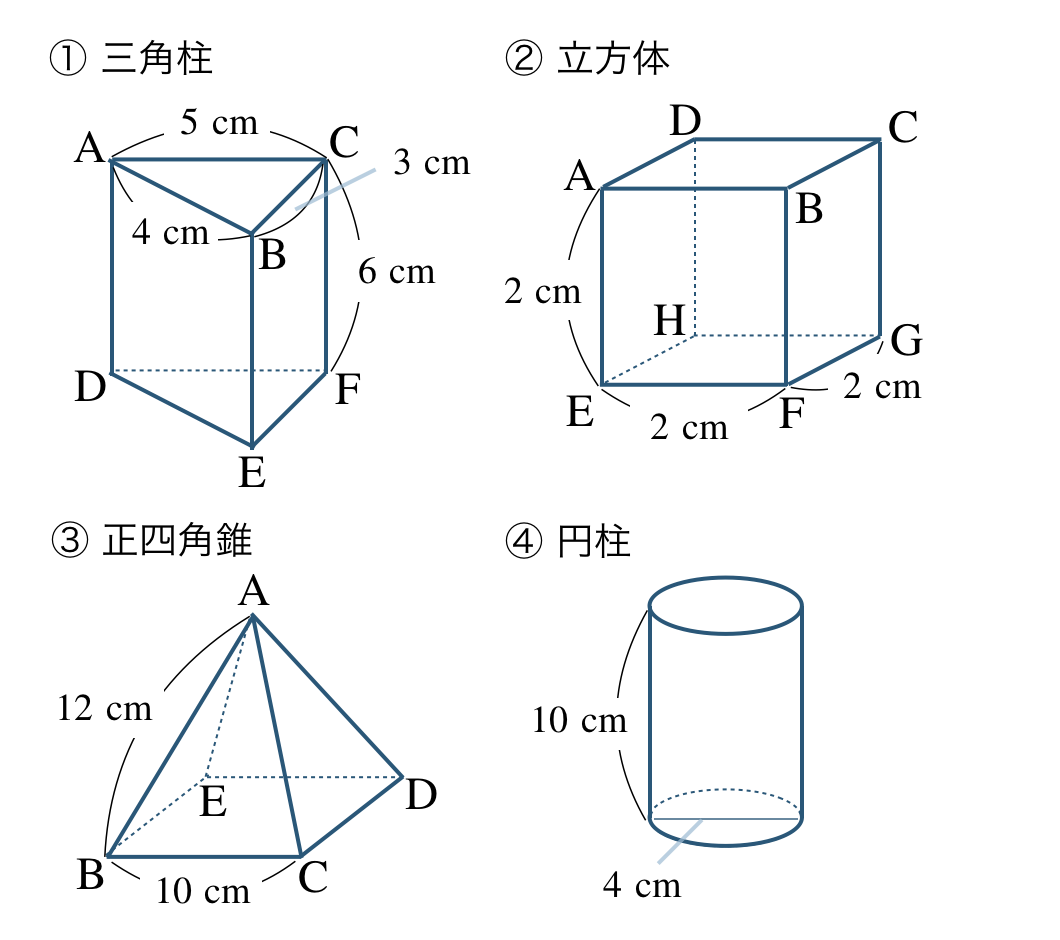
{\small (1)}~次の立体の展開図をかけ。
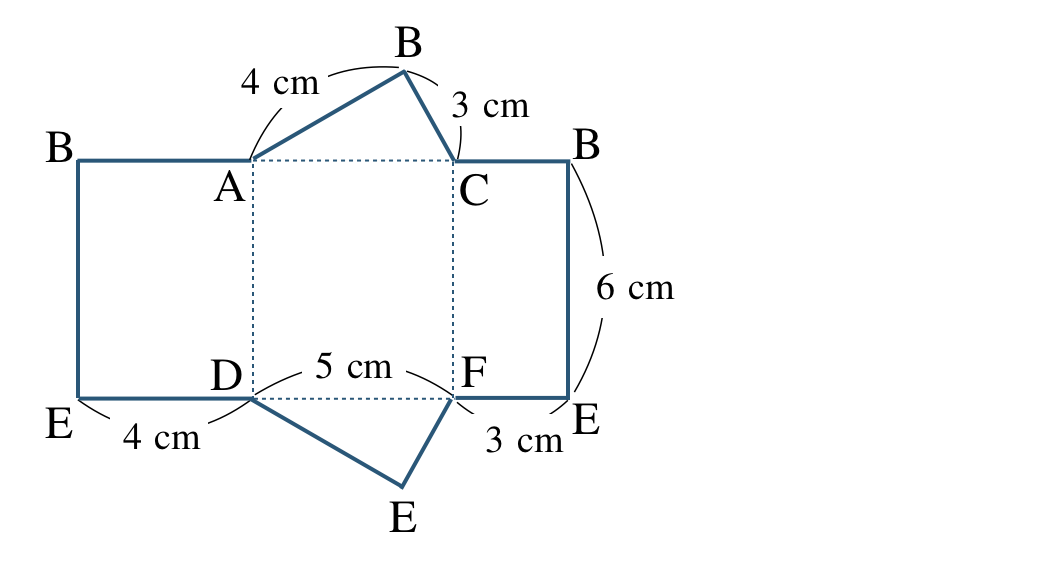
① 底面が三角形で、側面が長方形であり、\begin{split}~~~&{\rm AB=DE}=4~{\rm cm}\\[2pt]~~~&{\rm BC=EF}=3~{\rm cm}\\[2pt]~~~&{\rm AC=DF}=5~{\rm cm}\\[2pt]~~~&{\rm AD=BE=CF}=6~{\rm cm}\end{split}であるので、
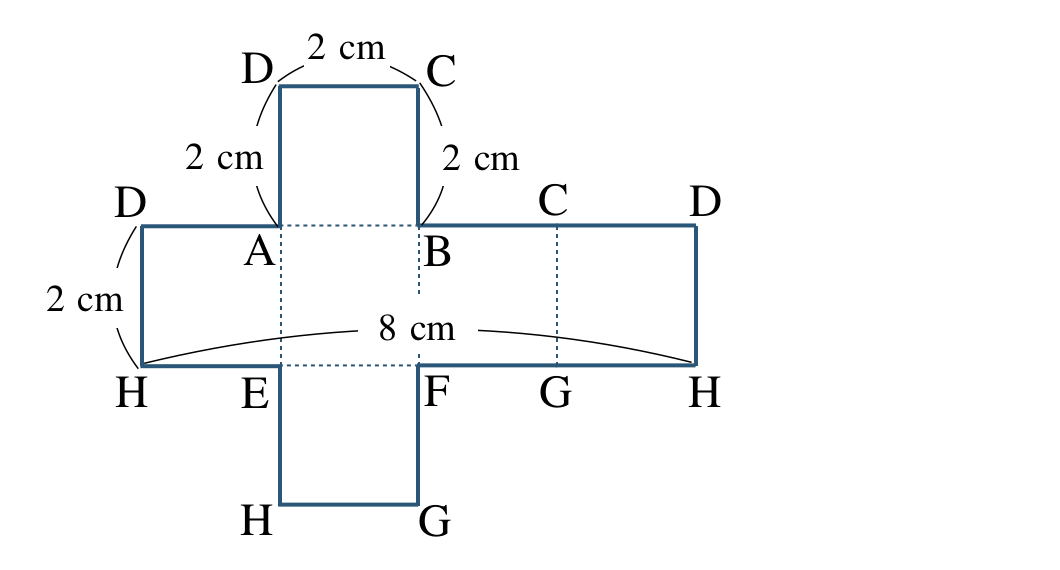
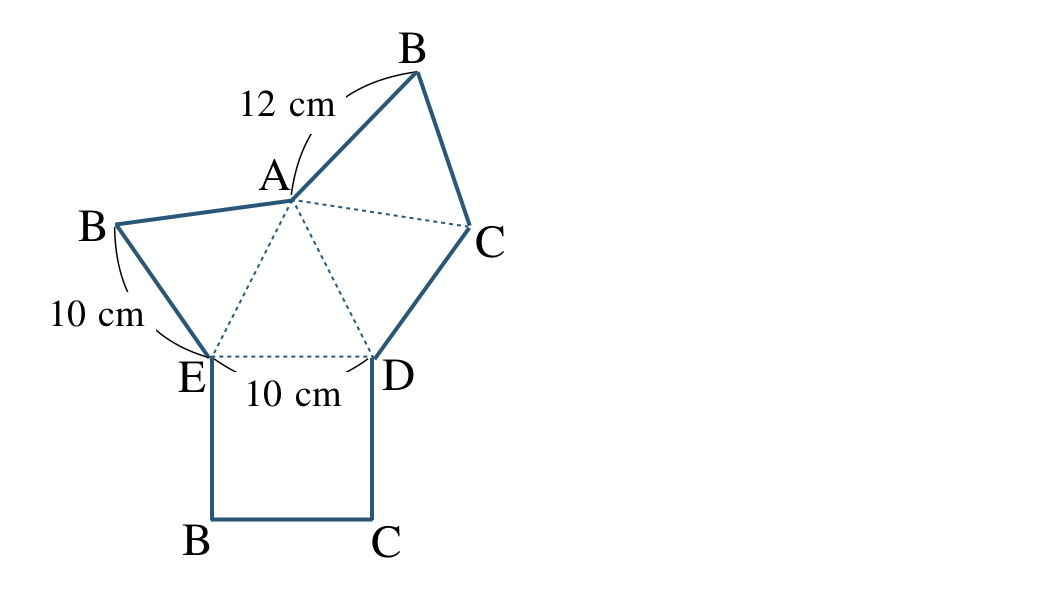
② すべての面が正方形であり、すべての辺の長さが 2~{\rm cm} であるので、
③ 底面が正方形で、側面が二等辺三角形であり、\begin{split}~~~&{\rm BC=CD=DE=BE}=10~{\rm cm}\\[2pt]~~~&{\rm AB=AC=AD=AE}=12~{\rm cm}\end{split}であるので、
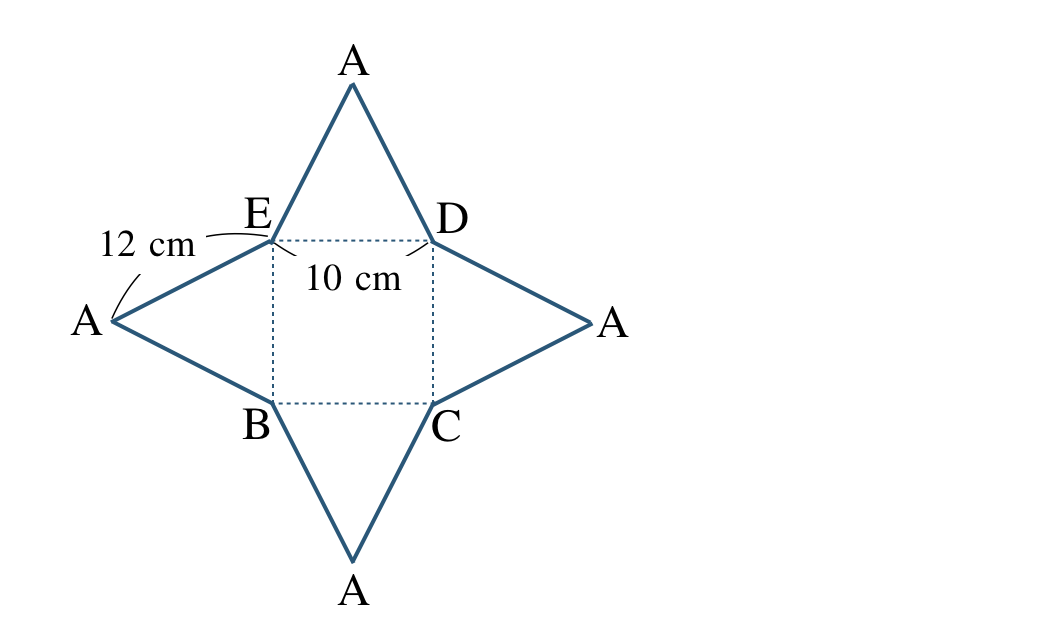
また、
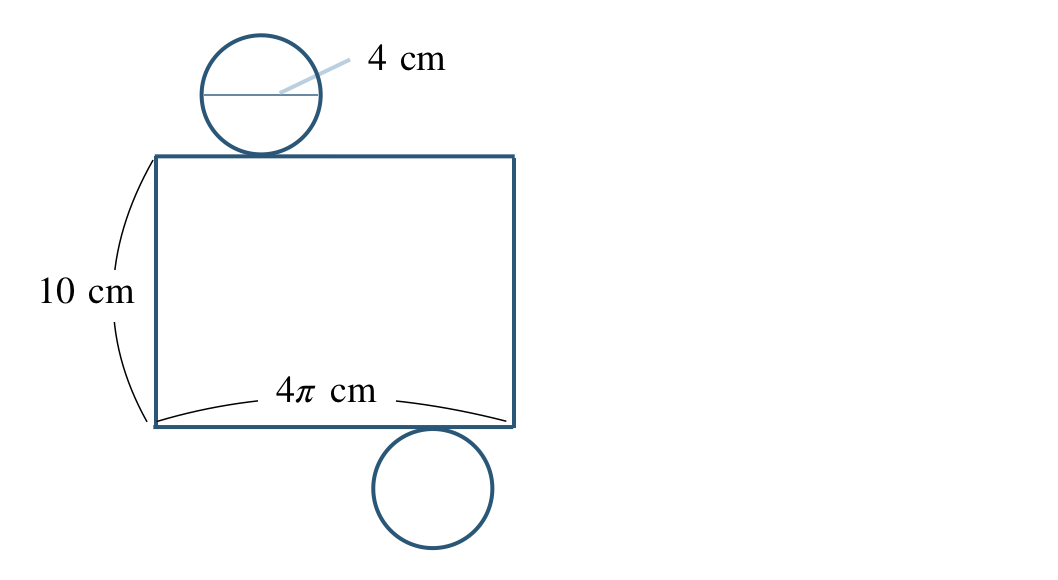
④ 底面が円で、側面が長方形であり、
長方形の横の長さは、底面の円の円周の長さとなるので、~~~4{\, \small \times \,} \pi=4\pi~{\rm cm}となるので、
問題解説(2)
次の問いに答えよ。
{\small (2)}~次の円錐について、
① この円錐の展開図で、側面となるおうぎ形の弧の長さと中心角を求めよ。
② この円錐の展開図をかけ。
① 円錐について、
側面のおうぎ形の弧の長さは、底面の円 {\rm O’} の円周の長さとなるので、~~~4{\, \small \times \,} 2 {\, \small \times \,} \pi =8\pi ~{\rm cm}また、円 {\rm O} の円周の長さは、~~~12{\, \small \times \,} 2 {\, \small \times \,} \pi =24\pi ~{\rm cm}これより、中心角 x^\circ は、\begin{eqnarray}~~~x&=&360^\circ {\, \small \times \,} \frac{\,8\pi\,}{\,24\pi\,}\\[3pt]~~~&=&360^\circ {\, \small \times \,} \frac{\,1\,}{\,3\,}\\[3pt]~~~&=&120^\circ\end{eqnarray}したがって、
弧の長さ 8\pi~{\rm cm}、中心角 120^\circ
となる
② 側面が半径 12~{\rm cm}、弧の長さ 8\pi~{\rm cm}、中心角 120^\circ のおうぎ形で、底面が半径 4~{\rm cm} の円より、
