問題:立体の表面積
問題
\({\small (1)}~\)次の立体の表面積を求めよ。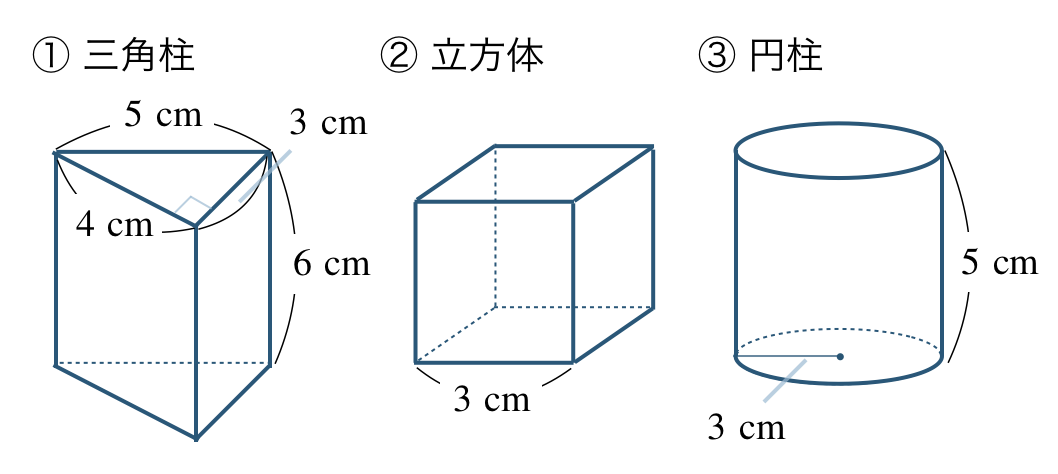
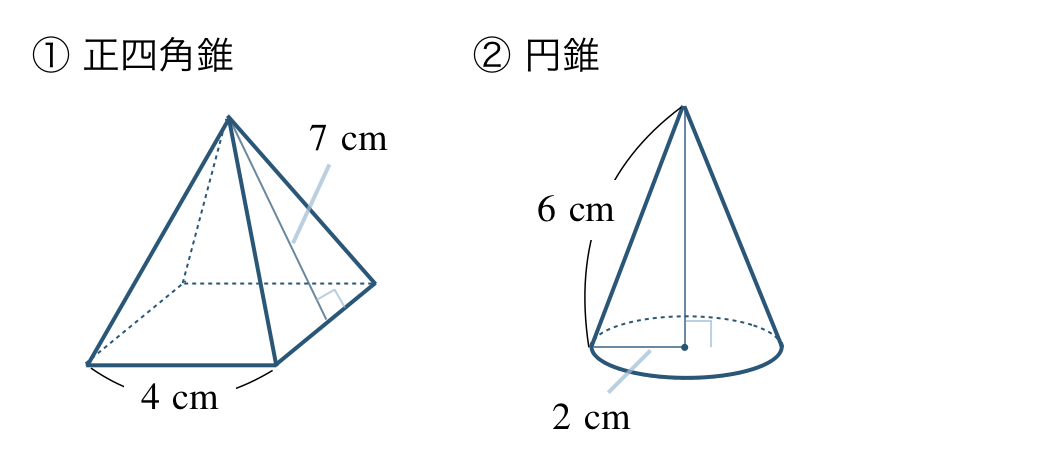
次の問いに答えよ。
\({\small (1)}~\)次の立体の表面積を求めよ。

\({\small (2)}~\)次の立体の表面積を求めよ。

解法のPoint
Point:角柱と角錐の表面積
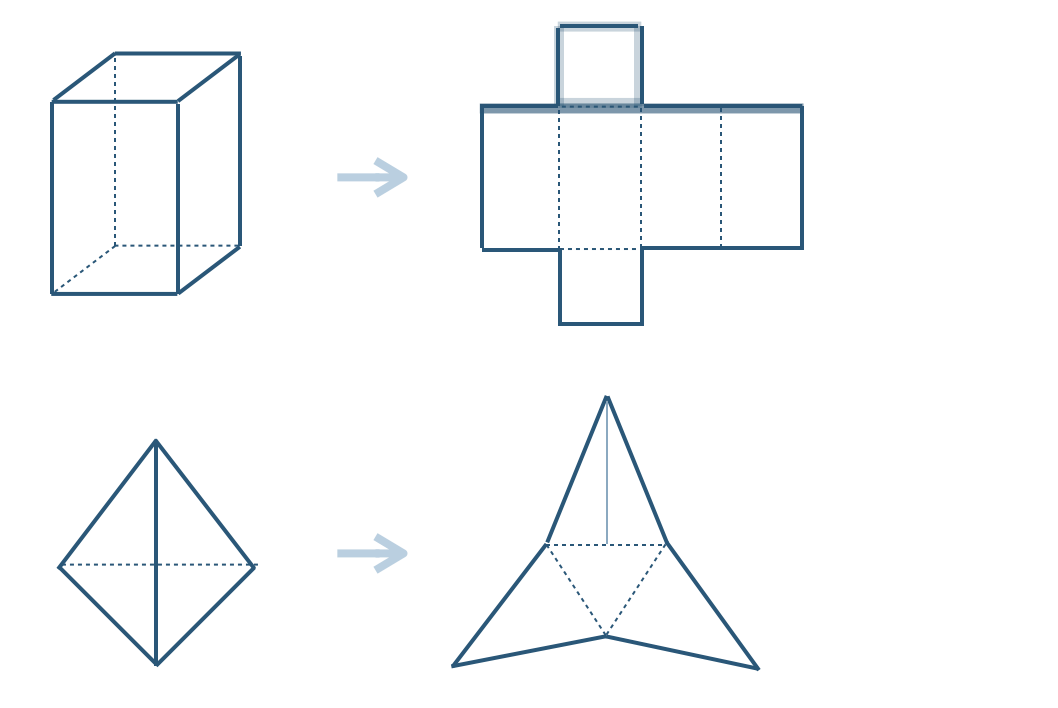
(側面積) + (底面積)\({\, \small \times \,}~2\)
※ 側面積の横の長さは、底面の周の長さとなる。
角錐の表面積は展開図より、
(側面積) + (底面積)
立体のすべての面の面積の和を「表面積」といい、側面全体の面積を「側面積」、1つの底面の面積を「底面積」という。

角柱の表面積は展開図より、
(側面積) + (底面積)\({\, \small \times \,}~2\)
※ 側面積の横の長さは、底面の周の長さとなる。
角錐の表面積は展開図より、
(側面積) + (底面積)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:円柱と円錐の表面積
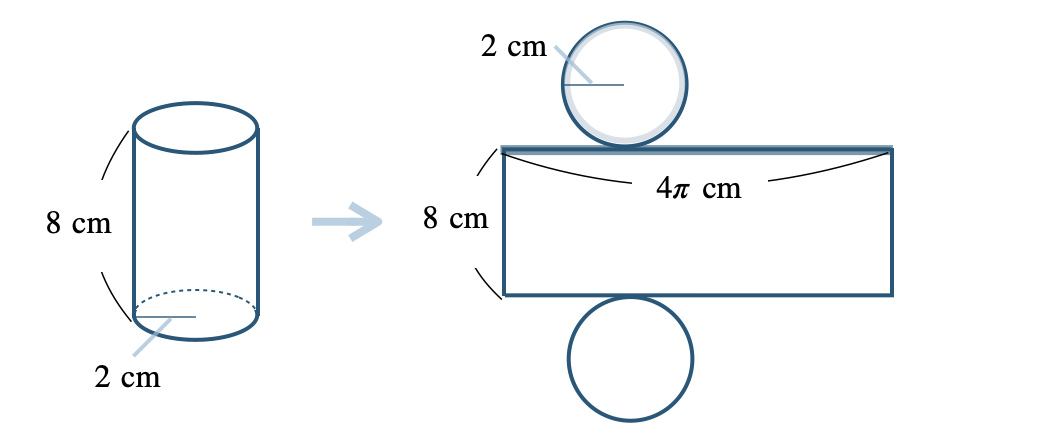
底面積は、\(\begin{split}(2{\, \small \times \,}2{\, \small \times \,}\pi){\, \small \times \,}2=8\pi~{\rm cm}^2\end{split}\)
よって、表面積は \(\begin{split}32\pi+8\pi=40\pi~{\rm cm}^2\end{split}\)
■ 円錐の表面積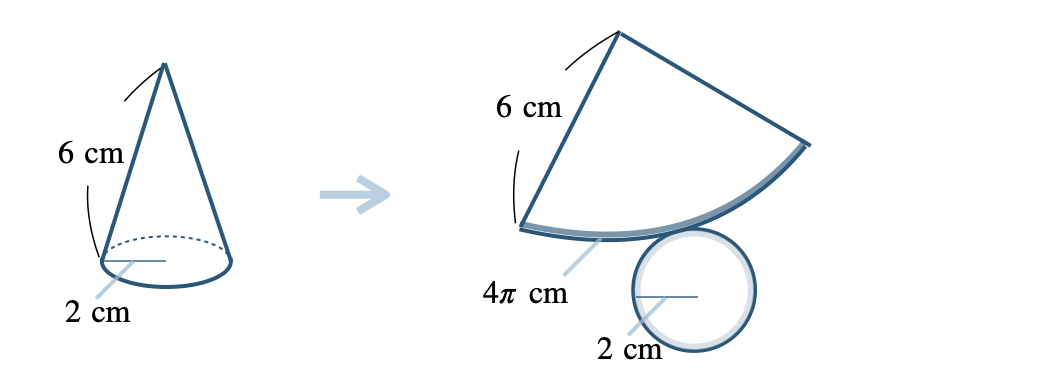
おうぎ形の面積(側面積)は、
(母線の長さ) × (おうぎ形の弧の長さ) ÷ 2
\(\begin{split}6{\, \small \times \,}4\pi{\, \small \div \,}2=12\pi~{\rm cm}^2\end{split}\)
また、底面積は、\(\begin{split}2{\, \small \times \,}2{\, \small \times \,}\pi=4\pi~{\rm cm}^2\end{split}\)
よって、表面積は \(\begin{split}12\pi+4\pi=16\pi~{\rm cm}^2\end{split}\)
■ 円柱の表面積

(長方形の横の長さ)=(円周の長さ)より、
側面積は、\(\begin{split}8{\, \small \times \,}4\pi=32\pi~{\rm cm}^2\end{split}\)
底面積は、\(\begin{split}(2{\, \small \times \,}2{\, \small \times \,}\pi){\, \small \times \,}2=8\pi~{\rm cm}^2\end{split}\)
よって、表面積は \(\begin{split}32\pi+8\pi=40\pi~{\rm cm}^2\end{split}\)
■ 円錐の表面積

(おうぎ形の弧の長さ)=(円周の長さ)となり、
おうぎ形の面積(側面積)は、
(母線の長さ) × (おうぎ形の弧の長さ) ÷ 2
\(\begin{split}6{\, \small \times \,}4\pi{\, \small \div \,}2=12\pi~{\rm cm}^2\end{split}\)
また、底面積は、\(\begin{split}2{\, \small \times \,}2{\, \small \times \,}\pi=4\pi~{\rm cm}^2\end{split}\)
よって、表面積は \(\begin{split}12\pi+4\pi=16\pi~{\rm cm}^2\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:立体の表面積
問題解説(1)
問題
\({\small (1)}~\)次の立体の表面積を求めよ。
次の問いに答えよ。
\({\small (1)}~\)次の立体の表面積を求めよ。

① この立体の展開図は、
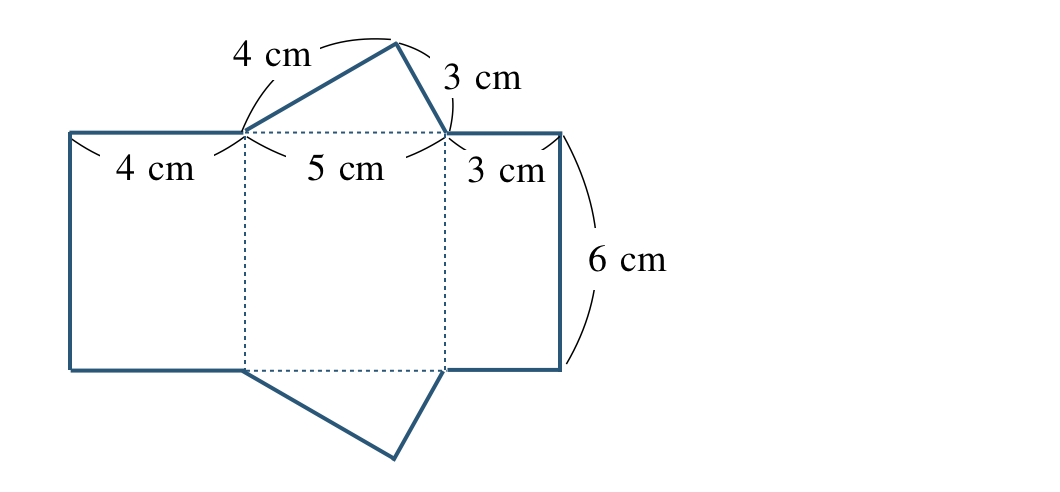
側面は、縦の長さ \(6~{\rm cm}\)、横の長さ \(4+5+3~{\rm cm}\) の長方形より、
\(\begin{split}~~~6{\, \small \times \,}(4+5+3)=6{\, \small \times \,} 12=72~{\rm cm}^2\end{split}\)
底面の1つは、\(4~{\rm cm}~,~3~{\rm cm}\) の直角三角形であるので、
\(\begin{split}~~~4{\, \small \times \,}3{\, \small \times \,}\frac{\,1\,}{\,2\,}=6~{\rm cm}^2\end{split}\)
表面積は、(側面積)+(底面積)\({\, \small \times \,}2\) であるので、
\(\begin{split}~~~72+6{\, \small \times \,} 2=72+12=84~{\rm cm}^2\end{split}\)
したがって、表面積 \(84~{\rm cm}^2\) となる
② この立体の展開図は、
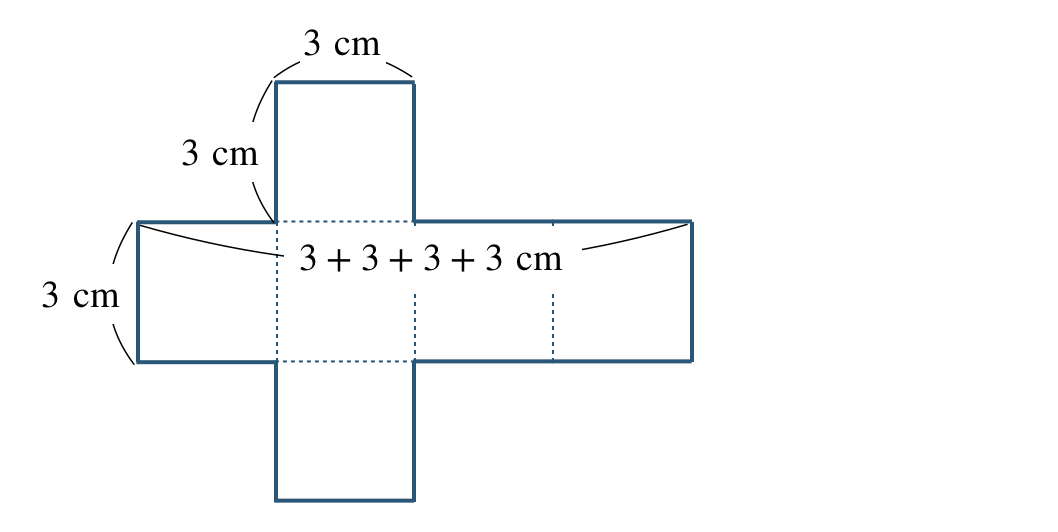
側面は、縦の長さ \(3~{\rm cm}\)、横の長さ \(3+3+3+3~{\rm cm}\) の長方形より、
\(\begin{split}~~~3{\, \small \times \,}(3+3+3+3)=3{\, \small \times \,} 12=36~{\rm cm}^2\end{split}\)
底面の1つは、1辺 \(3~{\rm cm}\) の正方形であるので、
\(\begin{split}~~~3{\, \small \times \,}3=9~{\rm cm}^2\end{split}\)
表面積は、(側面積)+(底面積)\({\, \small \times \,}2\) であるので、
\(\begin{split}~~~36+9{\, \small \times \,} 2=36+18=54~{\rm cm}^2\end{split}\)
したがって、表面積 \(54~{\rm cm}^2\) となる
③ この立体の展開図は、
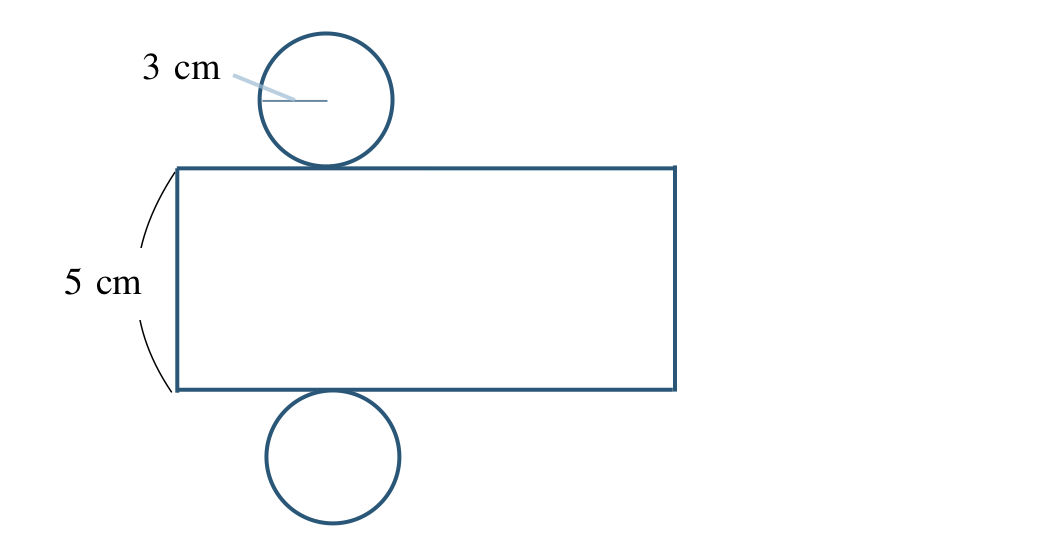
側面の長方形の横の長さは、底面の円の円周の長さと等しくなるので、
\(\begin{split}~~~3{\, \small \times \,}2{\, \small \times \,} \pi=6\pi~{\rm cm}\end{split}\)
また、縦の長さ \(5~{\rm cm}\) より、
\(\begin{split}~~~5{\, \small \times \,}6\pi=30\pi~{\rm cm}^2\end{split}\)
底面の1つは、半径 \(3~{\rm cm}\) の円であるので、
\(\begin{split}~~~3{\, \small \times \,}3{\, \small \times \,} \pi=9\pi~{\rm cm}^2\end{split}\)
表面積は、(側面積)+(底面積)\({\, \small \times \,}2\) であるので、
\(\begin{split}~~~30\pi+9\pi {\, \small \times \,} 2=30\pi+18\pi=48\pi~{\rm cm}^2\end{split}\)
したがって、表面積 \(48\pi~{\rm cm}^2\) となる
問題解説(2)
問題
\({\small (2)}~\)次の立体の表面積を求めよ。
次の問いに答えよ。
\({\small (2)}~\)次の立体の表面積を求めよ。

① この立体の展開図は、
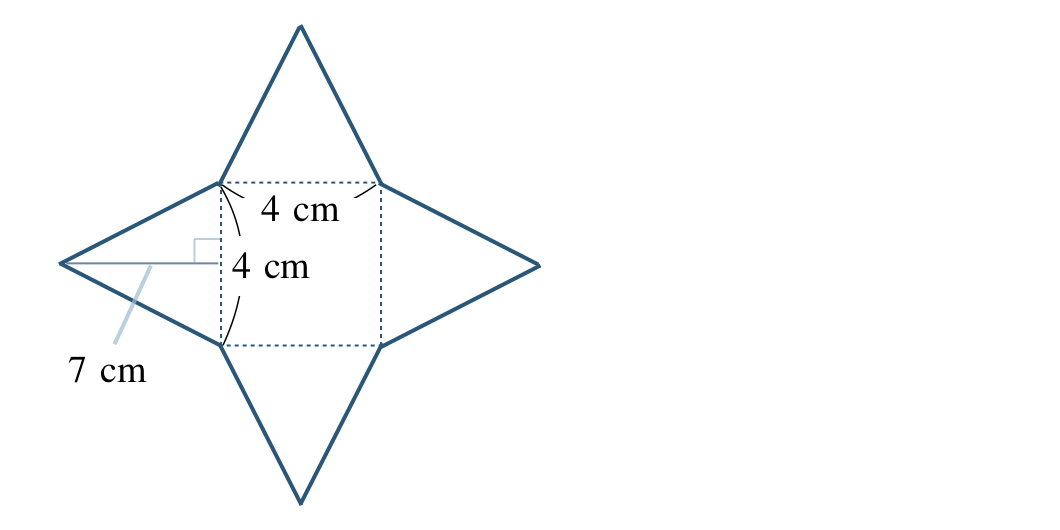
側面の1つは、底辺 \(4~{\rm cm}\)、高さ \(7~{\rm cm}\) の三角形であるので、
\(\begin{split}~~~4{\, \small \times \,}7{\, \small \times \,}\frac{\,1\,}{\,2\,}=14~{\rm cm}^2\end{split}\)
底面は、1辺 \(4~{\rm cm}\) の正方形であるので、
\(\begin{split}~~~4{\, \small \times \,}4=16~{\rm cm}^2\end{split}\)
展開図より、側面全体は三角形4つ分で底面は1つであるので、
表面積は、
\(\begin{split}~~~14{\, \small \times \,}4+16=56+16=72~{\rm cm}^2\end{split}\)
したがって、表面積 \(72~{\rm cm}^2\) となる
② この立体の展開図は、
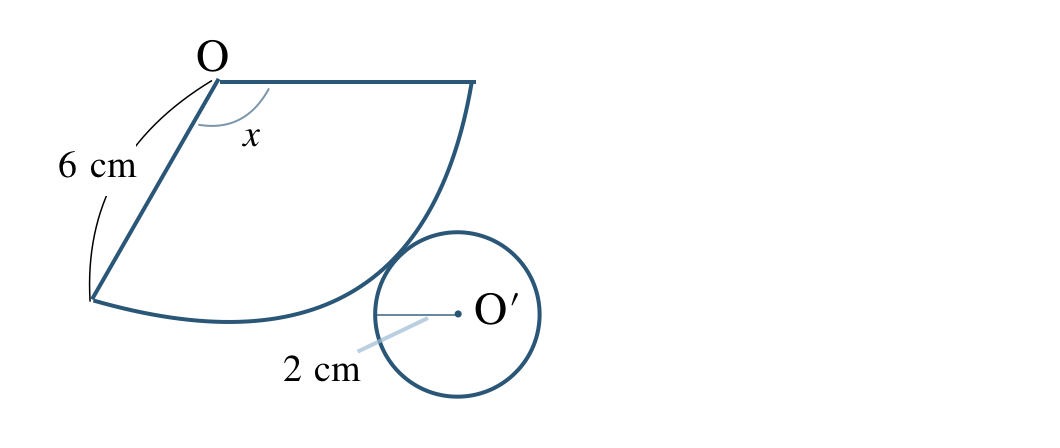
(おうぎ形の弧の長さ)=(底面の円の円周の長さ)より、半径 \(2~{\rm cm}\) の円であるので、
\(\begin{split}~~~2{\, \small \times \,}2{\, \small \times \,}\pi=4\pi~{\rm cm}\end{split}\)
おうぎ形の面積は、(母線の長さ) × (おうぎ形の弧の長さ) ÷ 2 より、
\(\begin{split}~~~6{\, \small \times \,}4\pi{\, \small \div \,}2=12\pi~{\rm cm}\end{split}\)
これより、側面積が \(12\pi~{\rm cm}^2\) となる
また、底面の円 \({\rm O’}\) は半径 \(2~{\rm cm}\) の円であるので、
\(\begin{split}~~~2{\, \small \times \,}2{\, \small \times \,}\pi=4\pi~{\rm cm}^2\end{split}\)
展開図より、
(表面積)=(側面積)+(底面積) となるので、
\(\begin{split}~~~12\pi+4\pi=16\pi~{\rm cm}^2\end{split}\)
したがって、表面積 \(16\pi~{\rm cm}^2\) となる
【別解】
※ 中心角を求めて、おうぎ形の面積を求める方法。
(おうぎ形の弧の長さ)=(底面の円の円周の長さ)より、半径 \(2~{\rm cm}\) の円であるので、
\(\begin{split}~~~2{\, \small \times \,}2{\, \small \times \,}\pi=4\pi~{\rm cm}\end{split}\)
また、円 \({\rm O}\) の円周の長さは、
\(\begin{split}~~~6{\, \small \times \,}2{\, \small \times \,}\pi=12\pi~{\rm cm}\end{split}\)
よって、おうぎ形の中心角 \(x^\circ\) は、
\(\begin{eqnarray}~~~x&=&360{\, \small \times \,}\frac{\,4\pi\,}{\,12\pi\,}\\[3pt]~~~&=&360{\, \small \times \,}\frac{\,1\,}{\,3\,}=120\end{eqnarray}\)
よって、中心角 \(120^\circ\) となる
また、おうぎ形の面積は円 \({\rm O}\) の面積 \(\begin{split}{\, \small \times \,}{\frac{\,120\,}{\,360\,}}\end{split}\) となるので、
\(\begin{split}~~~6{\, \small \times \,}6{\, \small \times \,} \pi{\, \small \times \,}\frac{\,120\,}{\,360\,}=36\pi{\, \small \times \,}\frac{\,1\,}{\,3\,}=12\pi~{\rm cm}^2\end{split}\)
これより、側面積が \(12\pi~{\rm cm}^2\) となる
また、底面の円 \({\rm O’}\) は半径 \(2~{\rm cm}\) の円であるので、
\(\begin{split}~~~2{\, \small \times \,}2{\, \small \times \,}\pi=4\pi~{\rm cm}^2\end{split}\)
展開図より、
(表面積)=(側面積)+(底面積) となるので、
\(\begin{split}~~~12\pi+4\pi=16\pi~{\rm cm}^2\end{split}\)
したがって、表面積 \(16\pi~{\rm cm}^2\) となる

【問題一覧】中1|空間図形
このページは「中学数学1 空間図形」の問題一覧ページとなります。解説の見たい単元名がわからないときは...


