問題:球の体積と表面積
問題
\({\small (1)}~\)次の球の体積と表面積を求めよ。
① 半径 \(6~{\rm cm}\)
② 直径 \(10~{\rm cm}\)
\({\small (2)}~\)次のおうぎ形を軸 \(l\) で回転させた立体の体積と表面積を求めよ。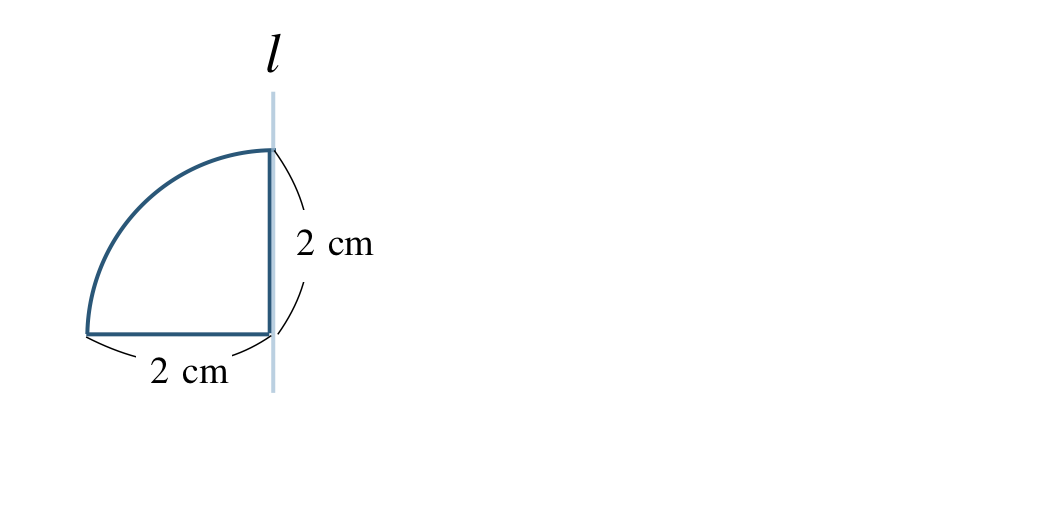
次の問いに答えよ。
\({\small (1)}~\)次の球の体積と表面積を求めよ。
① 半径 \(6~{\rm cm}\)
② 直径 \(10~{\rm cm}\)
\({\small (2)}~\)次のおうぎ形を軸 \(l\) で回転させた立体の体積と表面積を求めよ。

解法のPoint
Point:球の体積と表面積

\(\begin{split}V=\frac{\,4\,}{\,3\,}\pi r^3\end{split}\)
半径 \(r~{\rm cm}\) の球の表面積 \(S~{\rm cm}^2\) は、
\(\begin{split}S=4\pi r^2\end{split}\)
■ 球の体積と表面積

半径 \(r~{\rm cm}\) の球の体積 \(V~{\rm cm}^3\) は、
\(\begin{split}V=\frac{\,4\,}{\,3\,}\pi r^3\end{split}\)
半径 \(r~{\rm cm}\) の球の表面積 \(S~{\rm cm}^2\) は、
\(\begin{split}S=4\pi r^2\end{split}\)
となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:球の体積と表面積
問題解説(1)
問題
\({\small (1)}~\)次の球の体積と表面積を求めよ。
① 半径 \(6~{\rm cm}\)
② 直径 \(10~{\rm cm}\)
次の問いに答えよ。
\({\small (1)}~\)次の球の体積と表面積を求めよ。
① 半径 \(6~{\rm cm}\)
② 直径 \(10~{\rm cm}\)
① 半径 \(6~{\rm cm}\) より、
体積 \(V~{\rm cm}^3\) は、
\(\begin{eqnarray}~~~V&=&\frac{\,4\,}{\,3\,}\pi\times 6^3\\[3pt]~~~&=&\frac{\,4\,}{\,3\,}\pi\times216\\[3pt]~~~&=&4\pi\times72\\[2pt]~~~&=&288\pi~{\rm cm}^3\end{eqnarray}\)
表面積 \(S~{\rm cm}^2\) は、
\(\begin{eqnarray}~~~S&=&4\pi\times6^2\\[2pt]~~~&=&4\pi\times36\\[2pt]~~~&=&144\pi~{\rm cm}^2\end{eqnarray}\)
したがって、
体積 \(288~{\rm cm}^3\)、表面積 \(144~{\rm cm}^2\)
となる
② 直径 \(10~{\rm cm}\) より、半径は \(10\div2=5~{\rm cm}\) となる
体積 \(V~{\rm cm}^3\) は、
\(\begin{eqnarray}~~~V&=&\frac{\,4\,}{\,3\,}\pi\times 5^3\\[3pt]~~~&=&\frac{\,4\,}{\,3\,}\pi\times125\\[3pt]~~~&=&\frac{\,500\,}{\,3\,}\pi~{\rm cm}^3\end{eqnarray}\)
表面積 \(S~{\rm cm}^2\) は、
\(\begin{eqnarray}~~~S&=&4\pi\times5^2\\[2pt]~~~&=&4\pi\times25\\[2pt]~~~&=&100\pi~{\rm cm}^2\end{eqnarray}\)
したがって、
体積 \(\begin{split}{ \frac{\,500\,}{\,3\,}}\pi~{\rm cm}^3\end{split}\)、表面積 \(100\pi~{\rm cm}^2\)
となる
問題解説(2)
問題
\({\small (2)}~\)次のおうぎ形を軸 \(l\) で回転させた立体の体積と表面積を求めよ。
次の問いに答えよ。
\({\small (2)}~\)次のおうぎ形を軸 \(l\) で回転させた立体の体積と表面積を求めよ。

この回転体は、
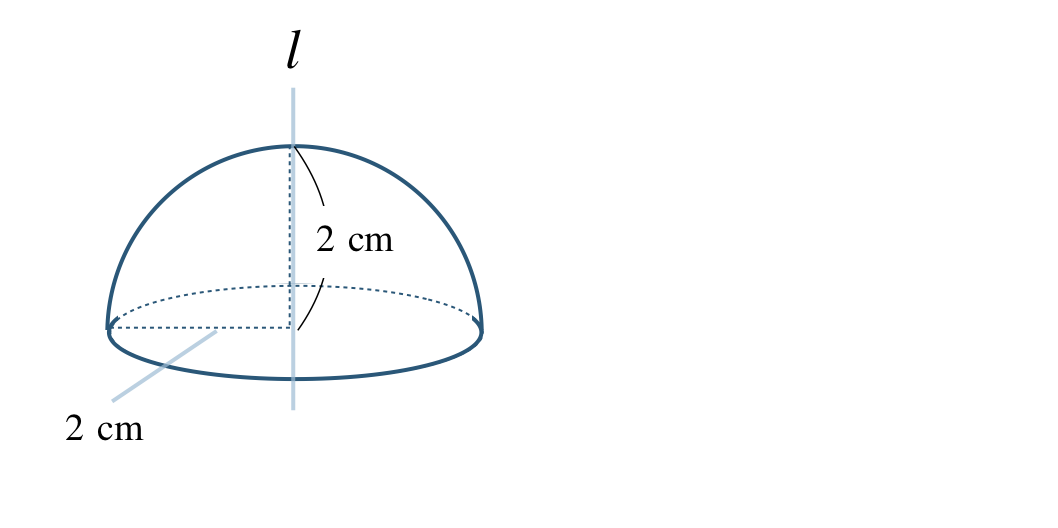
このように、球を半分にした立体となる
この立体の体積 \(V~{\rm cm}^3\) は、
(半径 \(2~{\rm cm}\) の球の体積) \(\div2\) より、
\(\begin{eqnarray}~~~V&=&\frac{\,4\,}{\,3\,}\pi\times2^3\div2\\[3pt]~~~&=&\frac{\,4\,}{\,3\,}\pi\times8\div2\\[3pt]~~~&=&\frac{\,4\,}{\,3\,}\pi\times4\\[3pt]~~~&=&\frac{\,16\,}{\,3\,}\pi~{\rm cm}^3\end{eqnarray}\)
また、立体の表面積 \(S~{\rm cm}^2\) は、
(球の表面積)\(\div2\) +(底面積)
となる
半径 \(2~{\rm cm}\) の球の表面積の半分より、
\(\begin{split}~~~4\pi\times2^2\div2=4\pi\times2=8\pi~{\rm cm}^2\end{split}\)
また、底面は半径 \(2~{\rm cm}\) の円より、
\(\begin{split}~~~2\times2\times\pi=4\pi~{\rm cm}^2\end{split}\)
よって、表面積は、
\(\begin{split}~~~8\pi+4\pi=12\pi~{\rm cm}^2\end{split}\)
したがって、
体積 \(\begin{split}{\frac{\,16\,}{\,3\,}}\pi~{\rm cm}^3\end{split}\)、表面積 \(12\pi~{\rm cm}^2\)
となる

【問題一覧】中1|空間図形
このページは「中学数学1 空間図形」の問題一覧ページとなります。解説の見たい単元名がわからないときは...


