2点を通る直線の式の解法
Point:2点を通る直線の式(傾き)
① 2点の座標から \(x\) の増加量と \(y\) の増加量を読みとり、傾きを求める。
傾きは、\(\begin{split}a=\frac{\,4-1\,}{\,5-2\,}=\frac{\,3\,}{\,3\,}=1\end{split}\)
② 求めた傾き \(a\) と一方の点の座標を代入することで、切片 \(b\) を求める。
\(a=1\) より、\(y=x+b\) となり、
\(x=2~,~y=1\) を代入すると、
\(\begin{eqnarray}~~~1&=&2+b\\[2pt]~~~b&=&-1\end{eqnarray}\)
※ \(x=5~,~y=4\) を代入してもよい。
③ 傾き \(a\)、切片 \(b\) より、直線の式を求める。
\(\begin{eqnarray}~~~y=x-1\end{eqnarray}\)
2点 \((2~,~1)~,~(5~,~4)\) を通る直線の式は、
① 2点の座標から \(x\) の増加量と \(y\) の増加量を読みとり、傾きを求める。

\(x\) の増加量は \(5-2\)、\(y\) の増加量は \(4-1\)
傾きは、\(\begin{split}a=\frac{\,4-1\,}{\,5-2\,}=\frac{\,3\,}{\,3\,}=1\end{split}\)
② 求めた傾き \(a\) と一方の点の座標を代入することで、切片 \(b\) を求める。
\(a=1\) より、\(y=x+b\) となり、
\(x=2~,~y=1\) を代入すると、
\(\begin{eqnarray}~~~1&=&2+b\\[2pt]~~~b&=&-1\end{eqnarray}\)
※ \(x=5~,~y=4\) を代入してもよい。
③ 傾き \(a\)、切片 \(b\) より、直線の式を求める。
\(\begin{eqnarray}~~~y=x-1\end{eqnarray}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:2点を通る直線の式(連立方程式)
① 直線の式を \(y=ax+b\) として、2点をそれぞれ代入した式をつくる。
\(y=ax+b\) より、
\(x=2~,~y=1\) を代入すると、
\(\begin{eqnarray}~~~1=2a+b\end{eqnarray}\)
\(x=5~,~y=4\) を代入すると、
\(\begin{eqnarray}~~~4=5a+b\end{eqnarray}\)
② \(a~,~b\) の2つの方程式を連立方程式として、解 \(a~,~b\) を求める。
\(~~~\begin{eqnarray} \left\{\begin{array}{l}2a+b=1 \\5a+b=4 \end{array}\right.\end{eqnarray}\)
これより、解は \(a=1~,~b=-1\)
③ 傾き \(a\)、切片 \(b\) より、直線の式を求める。
\(\begin{eqnarray}~~~y=x-1\end{eqnarray}\)
2点 \((2~,~1)~,~(5~,~4)\) を通る直線の式は、
① 直線の式を \(y=ax+b\) として、2点をそれぞれ代入した式をつくる。
\(y=ax+b\) より、
\(x=2~,~y=1\) を代入すると、
\(\begin{eqnarray}~~~1=2a+b\end{eqnarray}\)
\(x=5~,~y=4\) を代入すると、
\(\begin{eqnarray}~~~4=5a+b\end{eqnarray}\)
② \(a~,~b\) の2つの方程式を連立方程式として、解 \(a~,~b\) を求める。
\(~~~\begin{eqnarray} \left\{\begin{array}{l}2a+b=1 \\5a+b=4 \end{array}\right.\end{eqnarray}\)
これより、解は \(a=1~,~b=-1\)
③ 傾き \(a\)、切片 \(b\) より、直線の式を求める。
\(\begin{eqnarray}~~~y=x-1\end{eqnarray}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:2点を通る直線の式
問題解説(1)
問題
\({\small (1)}~\)2点 \((1~,~2)~,~(2~,~5)\) を通る。
次の直線の式を求めよ。
\({\small (1)}~\)2点 \((1~,~2)~,~(2~,~5)\) を通る。
直線の式を \(y=ax+b\) として、
2点 \((1~,~2)~,~(2~,~5)\) より、この直線の傾き \(a\) は、
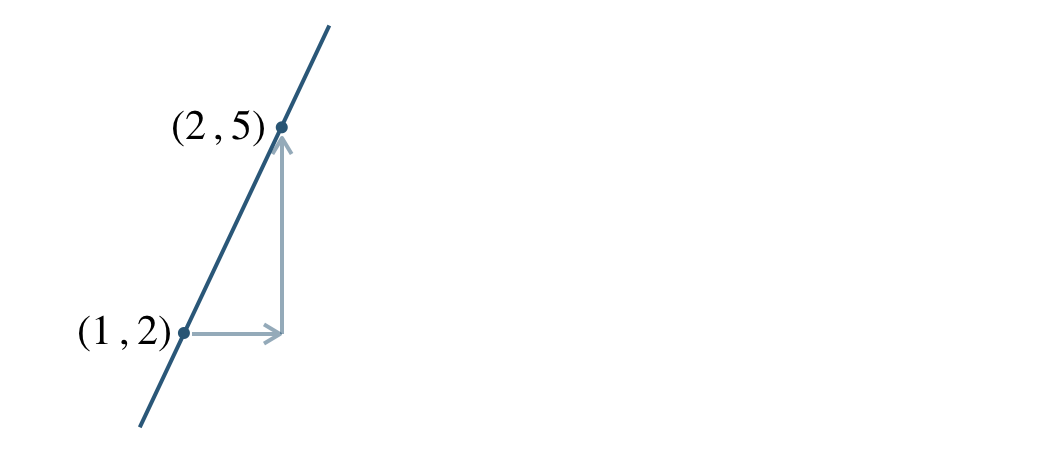
\(x\) の増加量は \(2-1\)、\(y\) の増加量は \(5-2\) より、
\(\begin{split}~~~a=\frac{\,5-2\,}{\,2-1\,}=\frac{\,3\,}{\,1\,}=3\end{split}\)
よって、\(y=3x+b\) となる
これに、点 \((1~,~2)\) を代入すると、
※ 点 \((2~,~5)\) を代入してもよい。
\(\begin{eqnarray}~~~2&=&3{\, \small \times \,}1+b\\[2pt]~~~2&=&3+b\\[2pt]~~~-b&=&3-2\\[2pt]~~~-b&=&1\\[2pt]~~~b&=&-1\end{eqnarray}\)
したがって、直線の式は \(\begin{split}y=3x-1\end{split}\) となる
【別解】
直線の式を \(y=ax+b\) として、
点 \((1~,~2)\) を通ることより、\(x=1~,~y=2\) を代入すると、
\(\begin{eqnarray}~~~2&=&a{\, \small \times \,} 1+b\\[2pt]~~~2&=&a+b\\[2pt]~~~a+b&=&2~~\cdots{\large ①}\end{eqnarray}\)
点 \((2~,~5)\) を通ることより、\(x=2~,~y=5\) を代入すると、
\(\begin{eqnarray}~~~5&=&a{\, \small \times \,} 2+b\\[2pt]~~~5&=&2a+b\\[2pt]~~~2a+b&=&5~~\cdots{\large ②}\end{eqnarray}\)
①と②を連立すると、
\(~~~\begin{eqnarray} \left\{\begin{array}{l}a+b=2 ~&\cdots{\large ①}\\2a+b=5 ~&\cdots{\large ②}\end{array}\right.\end{eqnarray}\)
②−①より、
\(~~~\begin{eqnarray}2a+b&=&5 \\-\big{)}~~ a+b &=&2\\\hline a+0&=&3\\a&=&3\end{eqnarray}\)
これを①に代入すると、
\(\begin{eqnarray}~~~3+b&=&2\\[2pt]~~~b&=&2-3\\[2pt]~~~b&=&-1\end{eqnarray}\)
したがって、直線の式は \(\begin{split}y=3x-1\end{split}\) となる
問題解説(2)
問題
\({\small (2)}~\)\(x=2\) のとき \(y=2\)、\(x=-4\) のとき \(y=5\) となる。
次の直線の式を求めよ。
\({\small (2)}~\)\(x=2\) のとき \(y=2\)、\(x=-4\) のとき \(y=5\) となる。
直線の式を \(y=ax+b\) として、
\(x=2\) のとき \(y=2\)、\(x=-4\) のとき \(y=5\) より、この直線の傾き \(a\) は、

\(x\) の増加量は \(-4-2\)、\(y\) の増加量は \(5-2\) より、
\(\begin{split}~~~a=\frac{\,5-2\,}{\,-4-2\,}=\frac{\,3\,}{\,-6\,}=-\frac{\,1\,}{\,2\,}\end{split}\)
よって、\(\begin{split}y=-{\frac{\,1\,}{\,2\,}}x+b\end{split}\) となる
これに、\(x=2\) のとき \(y=2\) となるので代入すると、
※ \(x=-4~,~y=5\) を代入してもよい。
\(\begin{eqnarray}~~~2&=&-\frac{\,1\,}{\,2\,}{\, \small \times \,}2+b\\[3pt]~~~2&=&-1+b\\[2pt]~~~-b&=&-1-2\\[2pt]~~~-b&=&-3\\[2pt]~~~b&=&3\end{eqnarray}\)
したがって、直線の式は \(\begin{split}y=-\frac{\,1\,}{\,2\,}x+3\end{split}\) となる
【別解】
直線の式を \(y=ax+b\) として、
\(x=2\) のとき \(y=2\) となるので代入すると、
\(\begin{eqnarray}~~~2&=&a{\, \small \times \,} 2+b\\[2pt]~~~2&=&2a+b\\[2pt]~~~2a+b&=&2~~\cdots{\large ①}\end{eqnarray}\)
\(x=-4\) のとき \(y=5\) となるので代入すると、
\(\begin{eqnarray}~~~5&=&a{\, \small \times \,} (-4)+b\\[2pt]~~~5&=&-4a+b\\[2pt]~~~4a-b&=&-5~~\cdots{\large ②}\end{eqnarray}\)
①と②を連立すると、
\(~~~\begin{eqnarray} \left\{\begin{array}{l}2a+b=2 ~&\cdots{\large ①}\\4a-b=-5 ~&\cdots{\large ②}\end{array}\right.\end{eqnarray}\)
①+②より、
\(~~~\begin{eqnarray}2a+b&=&2 \\+\big{)}~~ 4a-b &=&-5\\\hline 6a+0&=&-3\\6a&=&-3\end{eqnarray}\)
両辺を \(6\) で割ると、
\(\begin{eqnarray}\hspace{27pt}~~~\frac{\,6a\,}{\,6\,}&=&\frac{\,-3\,}{\,6\,}\\[3pt]~~~a&=&-\frac{\,1\,}{\,2\,}\end{eqnarray}\)
これを①に代入すると、
\(\begin{eqnarray}~~~2{\, \small \times \,}\left(-\frac{\,1\,}{\,2\,}\right)+b&=&2\\[2pt]~~~-1+b&=&2\\[2pt]~~~b&=&2+1\\[2pt]~~~b&=&3\end{eqnarray}\)
したがって、直線の式は \(\begin{split}y=-\frac{\,1\,}{\,2\,}x+3\end{split}\) となる

【問題一覧】中2|1次関数
このページは「中学数学2 1次関数」の問題一覧ページとなります。解説の見たい単元名がわからないときは...


