問題:1次関数と動く点
点 \({\rm P}\) は \(1\) 秒間に \(2~{\rm cm}\) で点 \({\rm B}\) →点 \({\rm A}\) →点 \({\rm D}\) →点 \({\rm C}\) と動く。\(x\) 秒後の \(\triangle {\rm PBC}\) の面積を \(y~{\rm cm}^2\) とするとき、次の問いに答えよ。
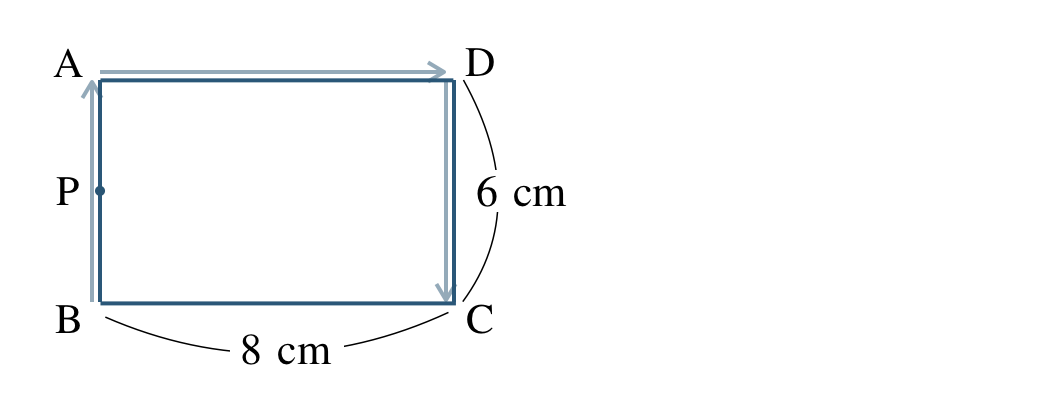
\({\small (1)}~\)点 \({\rm P}\) が辺 \({\rm AB}\) 上にあるとき、\(x\) の変域と \(y\) を \(x\) の式で表せ。
\({\small (2)}~\)点 \({\rm P}\) が辺 \({\rm AD}\) 上にあるとき、\(x\) の変域と \(y\) を \(x\) の式で表せ。
\({\small (3)}~\)点 \({\rm P}\) が辺 \({\rm CD}\) 上にあるとき、\(x\) の変域と \(y\) を \(x\) の式で表せ。
\({\small (4)}~\)点 \({\rm P}\) が点 \({\rm B}\) から点 \({\rm C}\) まで動くときの \(y\) と \(x\) の関係をグラフで表せ。
\({\small (5)}~\)\(\triangle {\rm PBC}\) の面積が \(16~{\rm cm}^2\) となるとき、点 \({\rm P}\) が点 \({\rm B}\) を出発して何秒後か答えよ。
解法のPoint
1辺 \(4~{\rm cm}\) の正方形 \({\rm ABCD}\) 上の辺を点 \({\rm P}\) が \({\rm A}\) から \({\rm B}\) に毎秒 \(1~{\rm cm}\) で動くとき、\(x\) 秒後の \(\triangle {\rm PBC}\) の面積 \(y~{\rm cm}^2\) の関数の求め方は、
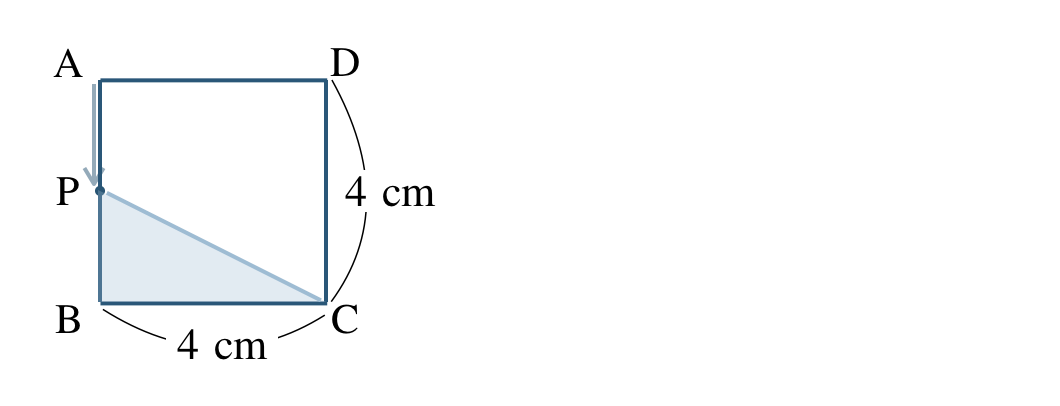
① \(x\) 秒後の図形より、面積 \(y~{\rm cm}^2\) を求める。
\({\rm AP}=x~{\rm cm}\) より、\({\rm PB}=4-x~{\rm cm}\)
よって、\(\triangle {\rm PBC}\) の面積 \(y~{\rm cm}^2\) は、
\(\begin{eqnarray}~y&=&\frac{\,1\,}{\,2\,}{\, \small \times \,}(4-x){\, \small \times \,}4
\\[3pt]~~~y&=&-2x+8
\end{eqnarray}\)
② \(x\) の変域を考えて、グラフをかく。
点 \({\rm P}\) は \({\rm A}\) から \({\rm B}\) に \(4\) 秒で進むので、
\(x\) の変域は、\(0≦x≦4\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:1次関数と動く点
問題解説(1)
点 \({\rm P}\) は \(1\) 秒間に \(2~{\rm cm}\) で点 \({\rm B}\) →点 \({\rm A}\) →点 \({\rm D}\) →点 \({\rm C}\) と動く。\(x\) 秒後の \(\triangle {\rm PBC}\) の面積を \(y~{\rm cm}^2\) とするとき、次の問いに答えよ。

\({\small (1)}~\)点 \({\rm P}\) が辺 \({\rm AB}\) 上にあるとき、\(x\) の変域と \(y\) を \(x\) の式で表せ。
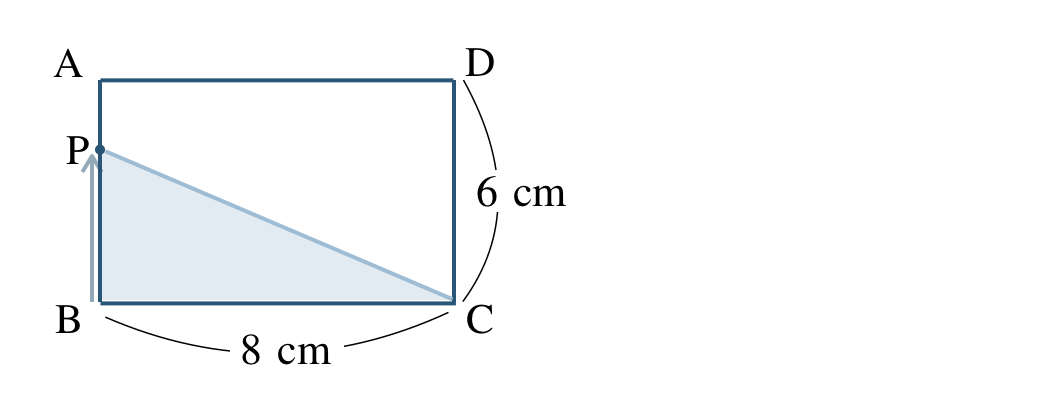
点 \({\rm P}\) は \(1\) 秒間に \(2~{\rm cm}\) 進むので、\(x\) 秒間に \(2x~{\rm cm}\) 進む
点 \({\rm P}\) が点 \({\rm A}\) に着くのは、\({\rm BA}=6~{\rm cm}\) 進んだときで、
時間=道のり÷速さより、
\(\begin{eqnarray}~~~2x&=&6\\[2pt]~~~x&=&3\end{eqnarray}\)
よって、\(3\) 秒後である
これより、\(x\) の変域は、\(\begin{split}0≦x≦3\end{split}\)
また、\(\triangle {\rm PBC}\) の面積 \(y~{\rm cm}^2\) は、
\(\begin{eqnarray}~~~y&=&\frac{\,1\,}{\,2\,}{\, \small \times \,}8{\, \small \times \,}2x\\[2pt]~~~y&=&8x\end{eqnarray}\)
したがって、
答えは \(\begin{split}y=8x~~,~~0≦x≦3\end{split}\) となる
問題解説(2)
点 \({\rm P}\) は \(1\) 秒間に \(2~{\rm cm}\) で点 \({\rm B}\) →点 \({\rm A}\) →点 \({\rm D}\) →点 \({\rm C}\) と動く。\(x\) 秒後の \(\triangle {\rm PBC}\) の面積を \(y~{\rm cm}^2\) とするとき、次の問いに答えよ。

\({\small (2)}~\)点 \({\rm P}\) が辺 \({\rm AD}\) 上にあるとき、\(x\) の変域と \(y\) を \(x\) の式で表せ。
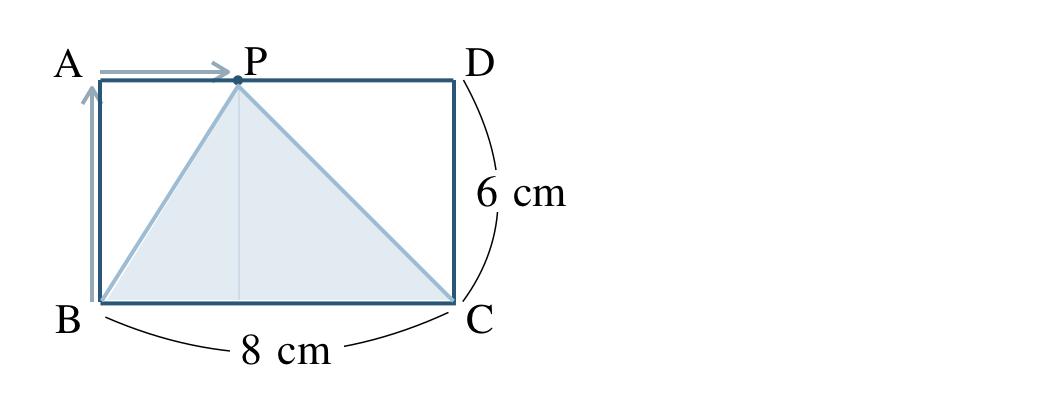
点 \({\rm P}\) は \(1\) 秒間に \(2~{\rm cm}\) 進むので、\(x\) 秒間に \(2x~{\rm cm}\) 進む
\({\small (1)}~\) より、点 \({\rm P}\) が点 \({\rm A}\) を出発するのは \(3\) 秒後
点 \({\rm D}\) に着くのは、\({\rm BA+AD}=14~{\rm cm}\) 進んだときで、
時間=道のり÷速さより、
\(\begin{eqnarray}~~~2x&=&14\\[2pt]~~~x&=&7\end{eqnarray}\)
よって、\(7\) 秒後である
これより、\(x\) の変域は、\(\begin{split}3≦x≦7\end{split}\)
また、\(\triangle {\rm PBC}\) の面積 \(y~{\rm cm}^2\) は、
\(\begin{eqnarray}~~~y&=&\frac{\,1\,}{\,2\,}{\, \small \times \,}8{\, \small \times \,}6\\[2pt]~~~y&=&24\end{eqnarray}\)
したがって、
答えは \(\begin{split}y=24~~,~~3≦x≦7\end{split}\) となる
問題解説(3)
点 \({\rm P}\) は \(1\) 秒間に \(2~{\rm cm}\) で点 \({\rm B}\) →点 \({\rm A}\) →点 \({\rm D}\) →点 \({\rm C}\) と動く。\(x\) 秒後の \(\triangle {\rm PBC}\) の面積を \(y~{\rm cm}^2\) とするとき、次の問いに答えよ。

\({\small (3)}~\)点 \({\rm P}\) が辺 \({\rm CD}\) 上にあるとき、\(x\) の変域と \(y\) を \(x\) の式で表せ。
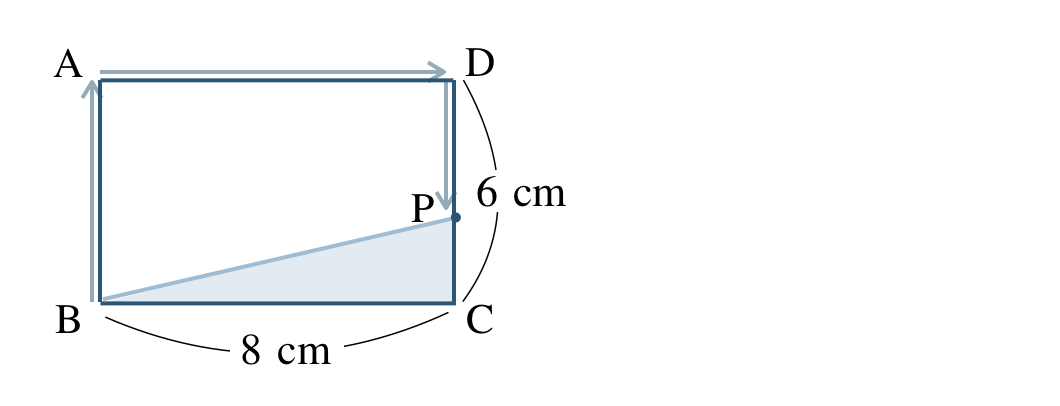
点 \({\rm P}\) は \(1\) 秒間に \(2~{\rm cm}\) 進むので、\(x\) 秒間に \(2x~{\rm cm}\) 進む
\({\small (2)}~\) より、点 \({\rm P}\) が点 \({\rm D}\) を出発するのは \(7\) 秒後
点 \({\rm C}\) に着くのは、\({\rm BA+AD+DC}=20~{\rm cm}\) 進んだときで、
時間=道のり÷速さより、
\(\begin{eqnarray}~~~2x&=&20\\[2pt]~~~x&=&10\end{eqnarray}\)
よって、\(10\) 秒後である
これより、\(x\) の変域は、\(\begin{split}7≦x≦10\end{split}\)
次に \({\rm PC}\) の長さは、
\(\begin{split}~~~{\rm BA+AD+DC}=6+8+6=20\end{split}\)
\(\begin{split}~~~{\rm BA+AD+DP}=2x\end{split}\)
であることより、\(\begin{split}{\rm PC}=20-2x\end{split}\)
よって、\(\triangle {\rm PBC}\) の面積 \(y~{\rm cm}^2\) は、
\(\begin{eqnarray}~~~y&=&\frac{\,1\,}{\,2\,}{\, \small \times \,}8{\, \small \times \,}(20-2x)\\[3pt]~~~y&=&4(20-2x)\\[2pt]~~~y&=&-8x+80\end{eqnarray}\)
したがって、
答えは \(\begin{split}y=-8x+80~~,~~7≦x≦10\end{split}\) となる
問題解説(4)
点 \({\rm P}\) は \(1\) 秒間に \(2~{\rm cm}\) で点 \({\rm B}\) →点 \({\rm A}\) →点 \({\rm D}\) →点 \({\rm C}\) と動く。\(x\) 秒後の \(\triangle {\rm PBC}\) の面積を \(y~{\rm cm}^2\) とするとき、次の問いに答えよ。

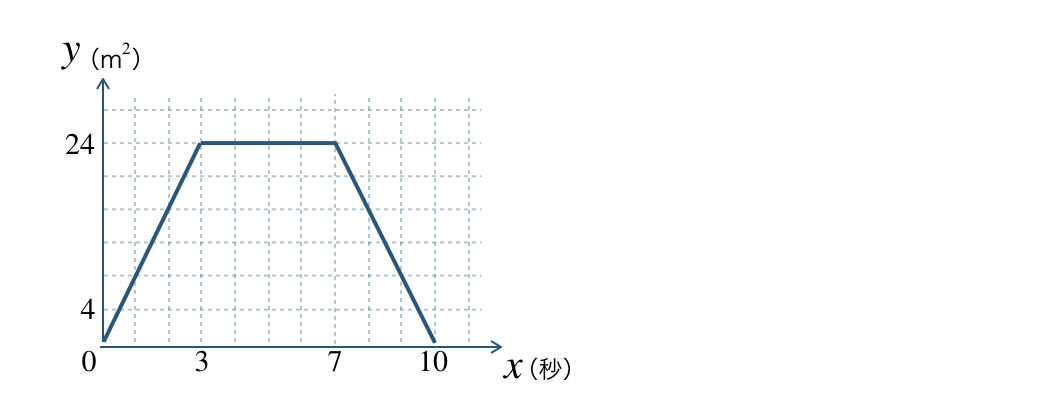
\({\small (4)}~\)点 \({\rm P}\) が点 \({\rm B}\) から点 \({\rm C}\) まで動くときの \(y\) と \(x\) の関係をグラフで表せ。
\({\small (1)}\) 〜 \({\small (3)}\) より、
\(0≦x≦3\) のとき、\(\begin{split}y=8x\end{split}\)
\(3≦x≦7\) のとき、\(\begin{split}y=24\end{split}\)
\(7≦x≦10\) のとき、\(\begin{split}y=-8x+80\end{split}\)
これより、
\(x=0\) のとき \(y=0\)
\(x=3\) のとき \(y=24\)
\(x=7\) のとき \(y=24\)
\(x=10\) のとき \(y=0\)
であるので、それぞれの点を結ぶと、
問題解説(5)
点 \({\rm P}\) は \(1\) 秒間に \(2~{\rm cm}\) で点 \({\rm B}\) →点 \({\rm A}\) →点 \({\rm D}\) →点 \({\rm C}\) と動く。\(x\) 秒後の \(\triangle {\rm PBC}\) の面積を \(y~{\rm cm}^2\) とするとき、次の問いに答えよ。

\({\small (5)}~\)\(\triangle {\rm PBC}\) の面積が \(16~{\rm cm}^2\) となるとき、点 \({\rm P}\) が点 \({\rm B}\) を出発して何秒後か答えよ。
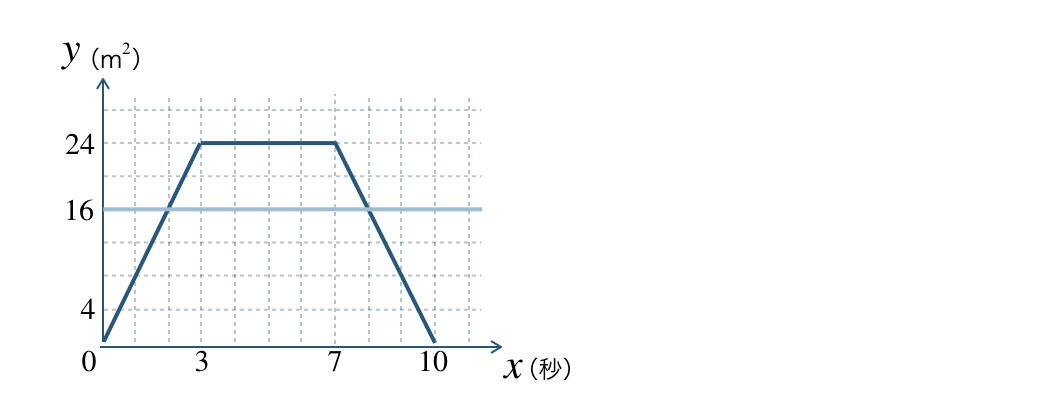
図より、\(y=16~{\rm cm}^2\) となるのは、
\(0≦x≦3\) のときと \(7≦x≦10\) のとき
(※ \(3≦x≦7\) のときはずっと \(y=24\) で \(y=16\) とならない)
\(0≦x≦3\) のとき \(y=8x\) より、\(y=16\) を代入すると、
\(\begin{eqnarray}~~~16&=&8x\\[2pt]~~~8x&=&16\\[3pt]~~~\frac{\,8x\,}{\,8\,}&=&\frac{\,16\,}{\,8\,}\\[3pt]~~~x&=&2\end{eqnarray}\)
\(7≦x≦10\) のとき \(y=-8x+80\) より、\(y=16\) を代入すると、
\(\begin{eqnarray}~~~16&=&-8x+80\\[2pt]~~~8x&=&80-16\\[2pt]~~~8x&=&64\\[3pt]~~~\frac{\,8x\,}{\,8\,}&=&\frac{\,64\,}{\,8\,}\\[3pt]~~~x&=&8\end{eqnarray}\)
よって、\(x=2~,~8\) となるので、
答えは 2秒後と8秒後 となる



