問題:平行線と角
次の問いに答えよ。
\({\small (1)}~\)次の角を記号で答えよ。
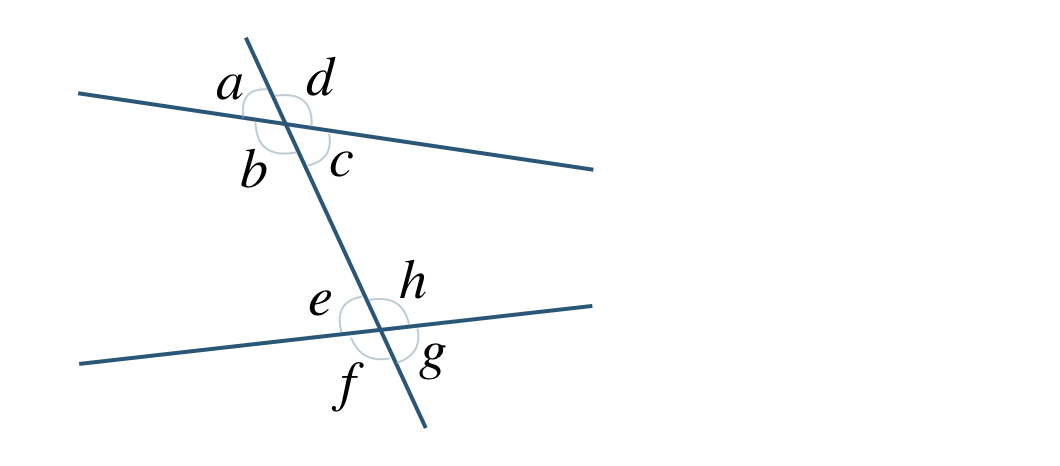
① \(\angle a\) の対頂角。
② \(\angle a\) の同位角。
③ \(\angle b\) の錯角。
④ \(\angle c\) の錯角。
\({\small (2)}~\)次の図において、
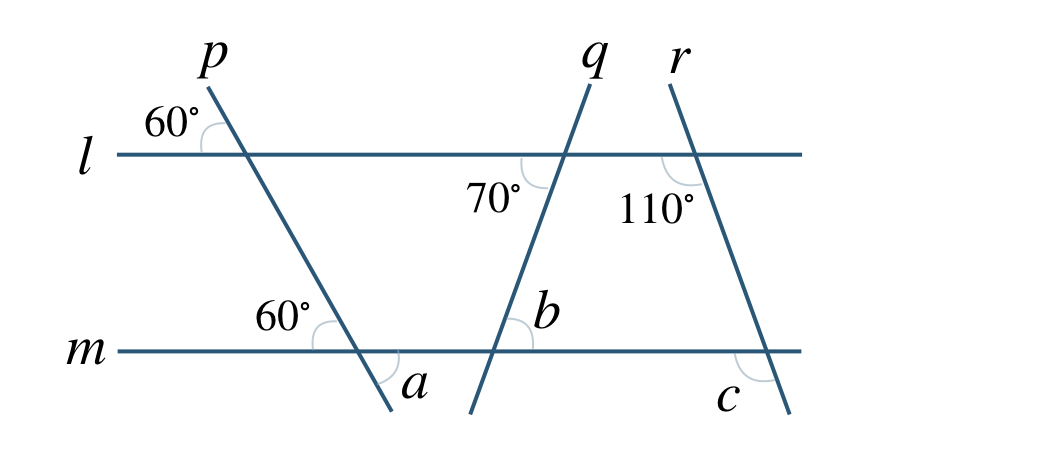
① \(l\,//\,m\) であることを説明せよ。
② \(\angle a~,~\angle b~,~\angle c\) の大きさを求めよ。
\({\small (3)}~\)次の図で \(l\,//\,m\) のとき、\(\angle x\) の大きさを求めよ。
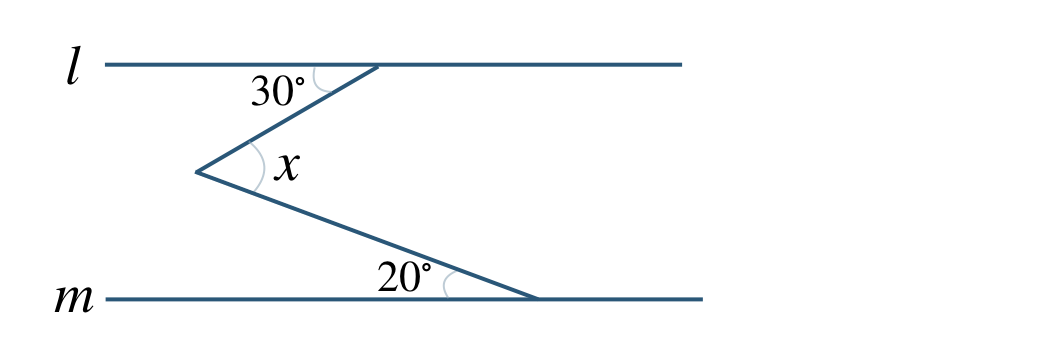
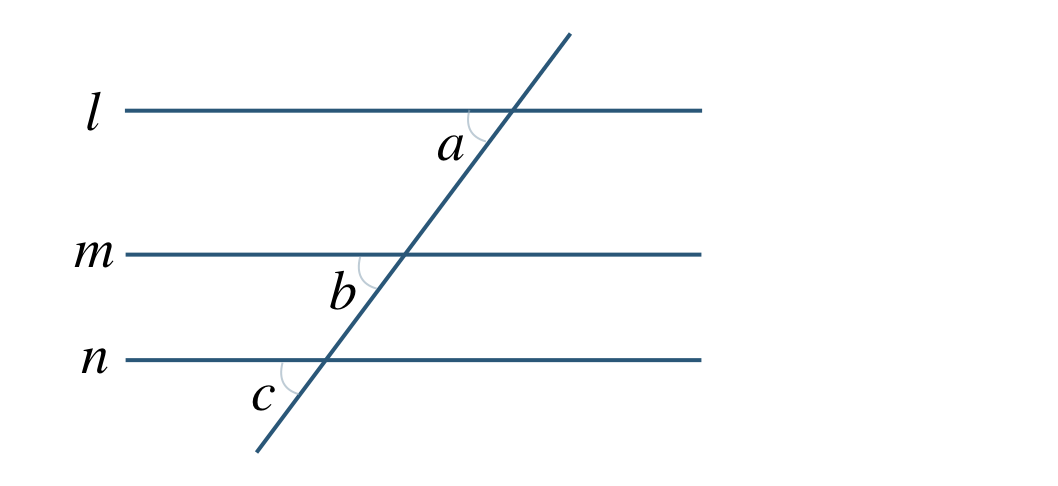
\({\small (4)}~\)次の図で、
\(l\,//\,m~,~l\,//\, n\) ならば \(m\,//\,n\)
を説明せよ。
解法のPoint
■ 2直線が交わるとき、

\(\angle a\) と \(\angle c\)、\(\angle b\) と \(\angle d\) のように、
向かい合う2つの角を「対頂角」といい、対頂角は等しくなる。
\(\angle a=\angle c~,~\angle b=\angle d\)
■ 2直線に1つの直線が交わるとき、
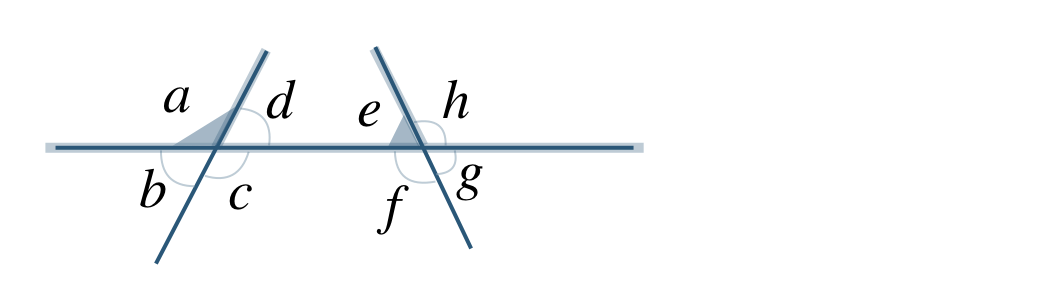
\(\angle a\) と \(\angle e\) のような位置にある角を「同位角」という。※ \(\angle b\) と \(\angle f\)、\(\angle c\) と \(\angle g\)、\(\angle d\) と \(\angle h\)

\(\angle d\) と \(\angle f\) のような位置にある角を「錯角」という。※ \(\angle c\) と \(\angle e\) も錯角である。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
2直線に1つの直線が交わるとき、
① 2直線が平行ならば同位角が等しい。
② 2直線が平行ならば錯角が等しい。
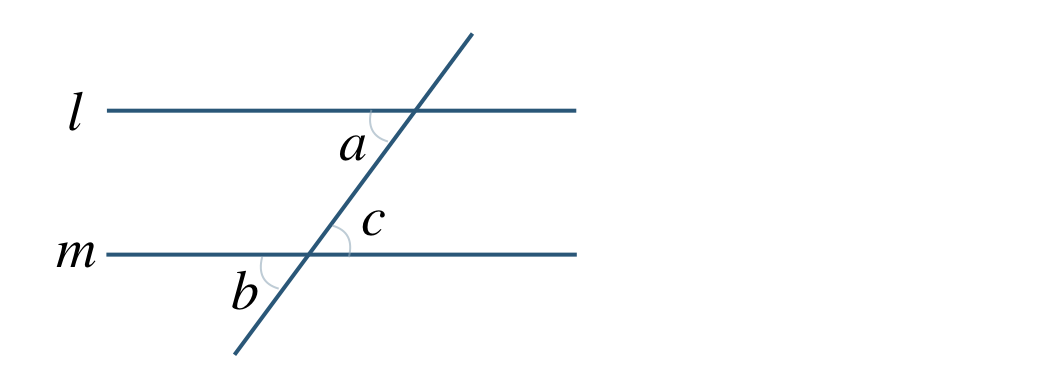
\(l\,//\,m\) のとき、
\(\angle a=\angle b\) (同位角が等しい)
\(\angle a=\angle c\) (錯角が等しい)
■ 平行線になるための条件
2直線に1つの直線が交わるとき、
① 同位角が等しいならば、2直線は平行である。
② 錯角が等しいならば、2直線は平行である。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:平行線と角
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の角を記号で答えよ。

① \(\angle a\) の対頂角。
② \(\angle a\) の同位角。
③ \(\angle b\) の錯角。
④ \(\angle c\) の錯角。
① \(\angle a\) の対頂角は、向かい合う角となるので、
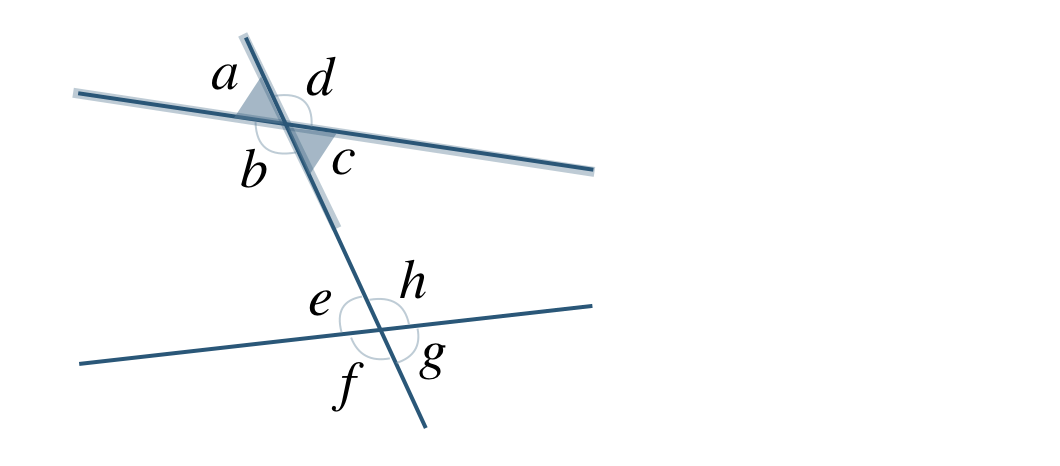
これより、\(\angle c\) となる
② \(\angle a\) の同位角は、直線上をスライドさせた位置の角であるので、
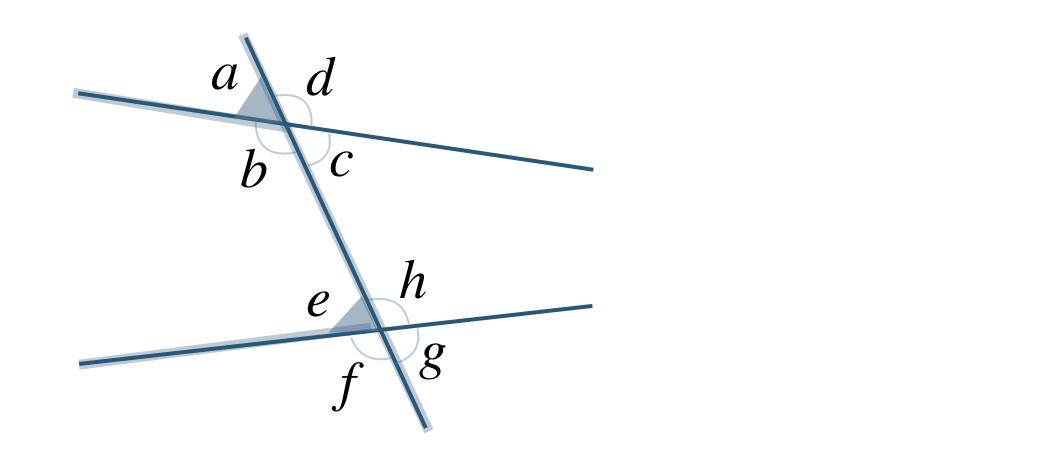
これより、\(\angle e\) となる
③ \(\angle b\) の錯角は、アルファベットのZの位置の角であるので、

これより、\(\angle h\) となる
④ \(\angle c\) の錯角は、アルファベットのZの位置の角であるので、
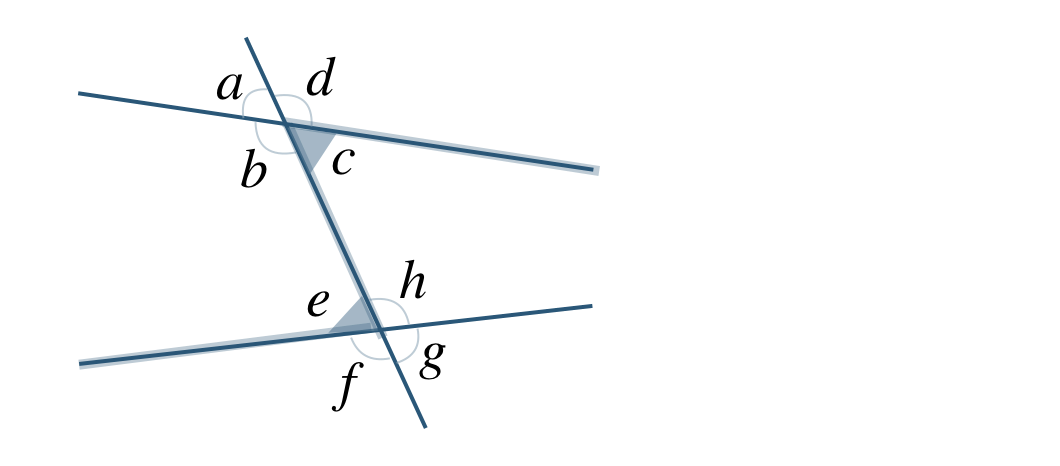
これより、\(\angle e\) となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の図において、

① \(l\,//\,m\) であることを説明せよ。
② \(\angle a~,~\angle b~,~\angle c\) の大きさを求めよ。
① 直線 \(p\) に対する同位角が \(60^\circ\) で等しいので、
2直線が平行となり、\(l\,//\,m\) となる
② 2直線 \(m~,~p\) の対頂角より、
\(\begin{split}~~~\angle a=60^\circ\end{split}\)
平行な2直線 \(l~,~m\) と直線 \(q\) の錯角より、
\(\begin{split}~~~\angle b=70^\circ\end{split}\)
平行な2直線 \(l~,~m\) と直線 \(r\) の同位角より、
\(\begin{split}~~~\angle c=110^\circ\end{split}\)
問題解説(3)
次の問いに答えよ。
\({\small (3)}~\)次の図で \(l\,//\,m\) のとき、\(\angle x\) の大きさを求めよ。

\(l~,~m\) と平行な補助線 \(n\) をひき、\(\angle x\) を \(\angle a\) と \(\angle b\) に分けると、
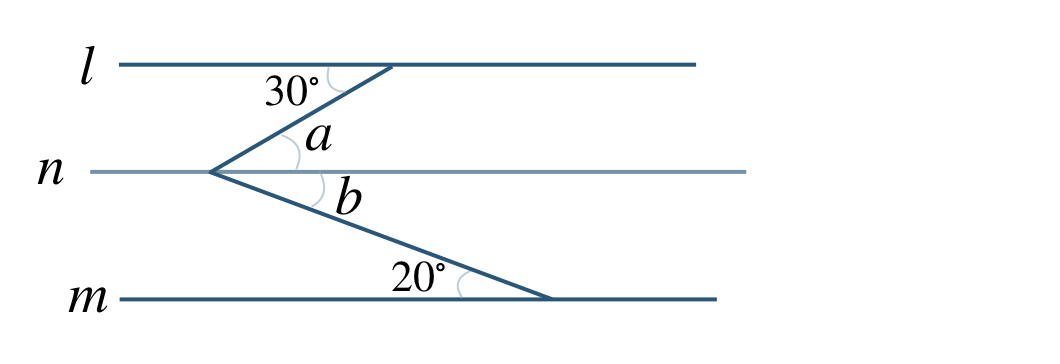
\(l\,//\,n\) の錯角より、
\(\begin{split}~~~\angle a=30^\circ\end{split}\)
\(n\,//\,m\) の錯角より、
\(\begin{split}~~~\angle b=20^\circ\end{split}\)
\(\angle x=\angle a+\angle b\) より、
\(\begin{split}~~~\angle x=30^\circ+20^\circ=50^\circ\end{split}\)
したがって、答えは \(\angle x=50^\circ\) となる
問題解説(4)
次の問いに答えよ。
\({\small (4)}~\)次の図で、
\(l\,//\,m~,~l\,//\, n\) ならば \(m\,//\,n\)
を説明せよ。

\(l\,//\,m\) の同位角が等しいことより、
\(\begin{split}~~~\angle a=\angle b\end{split}\)
\(l\,//\,n\) の同位角が等しいことより、
\(\begin{split}~~~\angle a=\angle c\end{split}\)
よって、
\(\begin{split}~~~\angle b=\angle c\end{split}\)
同位角が等しいので、2直線 \(m~,~n\) が平行となり、
\(\begin{split}~~~m\,//\,n\end{split}\)



