問題:多角形の内角と外角
問題
\({\small (1)}~\)十角形について、次の値を求めよ。
① 内角の和。
② 外角の和。
\({\small (2)}~\)正十二角形について、次の値を求めよ。
① 内角の和。
② 外角の和。
③ 1つの内角の大きさ。
④ 1つの外角の大きさ。
\({\small (3)}~\)次の条件の多角形を答えよ。
① 内角の和が \(1620^\circ\)。
② 1つの内角が \(135^\circ\) の正多角形。
\({\small (4)}~\)次の図において、\(\angle x\) の大きさを求めよ。
①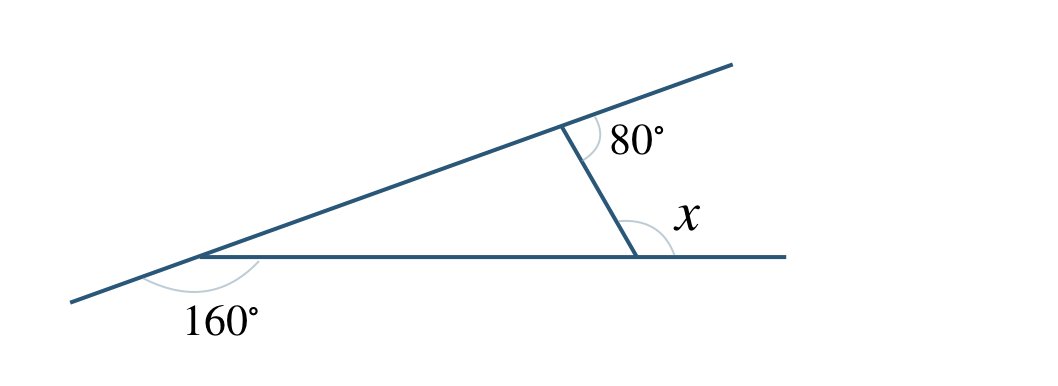
次の問いに答えよ。
\({\small (1)}~\)十角形について、次の値を求めよ。
① 内角の和。
② 外角の和。
\({\small (2)}~\)正十二角形について、次の値を求めよ。
① 内角の和。
② 外角の和。
③ 1つの内角の大きさ。
④ 1つの外角の大きさ。
\({\small (3)}~\)次の条件の多角形を答えよ。
① 内角の和が \(1620^\circ\)。
② 1つの内角が \(135^\circ\) の正多角形。
\({\small (4)}~\)次の図において、\(\angle x\) の大きさを求めよ。
①

②

解法のPoint
Point:多角形の内角と外角
よって、\(n\) 角形では \(n-2\) 個の三角形に分けられるので、\(n\) 角形の内角の和は、
\(180^\circ {\, \small \times \,} (n-2)\)
また、多角形の外角の和はどんな多角形でも同じとなるので、
多角形の外角の和 \(=360^\circ\)
多角形は1つの頂点からひいた対角線によって、いくつかの三角形に分けられる。
よって、\(n\) 角形では \(n-2\) 個の三角形に分けられるので、\(n\) 角形の内角の和は、
\(180^\circ {\, \small \times \,} (n-2)\)
また、多角形の外角の和はどんな多角形でも同じとなるので、
多角形の外角の和 \(=360^\circ\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:多角形の内角と外角
問題解説(1)
問題
\({\small (1)}~\)十角形について、次の値を求めよ。
① 内角の和。
② 外角の和。
次の問いに答えよ。
\({\small (1)}~\)十角形について、次の値を求めよ。
① 内角の和。
② 外角の和。
① 十角形は1つの頂点からひいた対角線によって、8つの三角形に分けられる
よって、内角の和は、
\(\begin{split}&180^\circ{\, \small \times \,}(10-2)\\[2pt]~~=~&180^\circ{\, \small \times \,}8\\[2pt]~~=~&1440^\circ\end{split}\)
したがって、答えは \(1440^\circ\) となる
② 多角形の外角の和はどんな多角形でも同じであるので、
答えは \(360^\circ\) となる
問題解説(2)
問題
\({\small (2)}~\)正十二角形について、次の値を求めよ。
① 内角の和。
② 外角の和。
③ 1つの内角の大きさ。
④ 1つの外角の大きさ。
次の問いに答えよ。
\({\small (2)}~\)正十二角形について、次の値を求めよ。
① 内角の和。
② 外角の和。
③ 1つの内角の大きさ。
④ 1つの外角の大きさ。
① 正十二角形は1つの頂点からひいた対角線によって、10個の三角形に分けられる
よって、内角の和は、
\(\begin{split}&180^\circ{\, \small \times \,}(12-2)\\[2pt]~~=~&180^\circ{\, \small \times \,}10\\[2pt]~~=~&1800^\circ\end{split}\)
したがって、答えは \(1800^\circ\) となる
② 多角形の外角の和はどんな多角形でも同じであるので、
答えは \(360^\circ\) となる
③ 正十二角形の内角はすべて等しく、12個の頂点がある
内角の和が \(1800^\circ\) であるので、1つの内角の大きさは、
\(~~~1800^\circ{\, \small \div \,}12=150^\circ\)
答えは \(150^\circ\) となる
④ 正十二角形の外角はすべて等しく、12個の頂点がある
外角の和が \(360^\circ\) であるので、1つの外角の大きさは、
\(~~~360^\circ{\, \small \div \,}12=30^\circ\)
答えは \(30^\circ\) となる
問題解説(3)
問題
\({\small (3)}~\)次の条件の多角形を答えよ。
① 内角の和が \(1620^\circ\)。
② 1つの内角が \(135^\circ\) の正多角形。
次の問いに答えよ。
\({\small (3)}~\)次の条件の多角形を答えよ。
① 内角の和が \(1620^\circ\)。
② 1つの内角が \(135^\circ\) の正多角形。
① この多角形を \(n\) 角形とすると、内角の和が \(1620^\circ\) となるので、
\(\begin{eqnarray}~~~180^\circ{\, \small \times \,}(n-2)&=&1620^\circ\\[3pt]~~~\frac{\,180^\circ{\, \small \times \,}(n-2)\,}{\,180^\circ\,}&=&\frac{\,1620^\circ\,}{\,180^\circ\,}\\[3pt]~~~n-2&=&9\\[2pt]~~~n&=&9+2\\[2pt]~~~n&=&11\end{eqnarray}\)
したがって、答えは 十一角形 となる
② この多角形を正 \(n\) 角形とする
1つの内角の大きさが \(135^\circ\) ですべて等しいので、\(n\) 個の内角の和は、
\(~~~135^\circ {\, \small \times \,} n=135^\circ n\)
また、\(n\) 角形の内角の和の公式 \(180^\circ {\, \small \times \,}(n-2)\) であるので、
\(\begin{eqnarray}~~~180^\circ {\, \small \times \,}(n-2)&=&135^\circ n\\[2pt]~~~180^\circ {\, \small \times \,} n+180^\circ{\, \small \times \,}(-2)&=&135^\circ n\\[2pt]~~~180^\circ n-360^\circ&=&135^\circ n\\[2pt]~~~180^\circ n-135^\circ n&=&360^\circ\\[2pt]~~~45^\circ n&=&360^\circ\\[3pt]~~~\frac{\,45^\circ n\,}{\,45^\circ\,}&=&\frac{\,360^\circ\,}{\,45^\circ\,}\\[3pt]~~~n&=&8\end{eqnarray}\)
したがって、答えは 正八角形 となる
【別解】
この多角形を正 \(n\) 角形とする
内角が \(135^\circ\) より、この多角形の外角は、
\(~~~180^\circ-135^\circ=45^\circ\)
外角の和は \(360^\circ\) より、
\(\begin{eqnarray}~~~360^\circ {\, \small \div \,}n&=&45^\circ\\[3pt]~~~\frac{\,45^\circ n\,}{\,45^\circ\,}&=&\frac{\,360^\circ\,}{\,45^\circ\,}\\[3pt]~~~n&=&8\end{eqnarray}\)
したがって、答えは 正八角形 となる
問題解説(4)
問題
\({\small (4)}~\)次の図において、\(\angle x\) の大きさを求めよ。
①

次の問いに答えよ。
\({\small (4)}~\)次の図において、\(\angle x\) の大きさを求めよ。
①

②

① 多角形の外角の和は \(180^\circ\) より、
\(\begin{eqnarray}~~~160^\circ+80^\circ+\angle x&=&360^\circ\\[2pt]~~~240^\circ+\angle x&=&360^\circ\\[2pt]~~~\angle x&=&360^\circ-240^\circ\\[2pt]~~~\angle x&=&120^\circ\end{eqnarray}\)
したがって、答えは \(\angle x=120^\circ\) となる
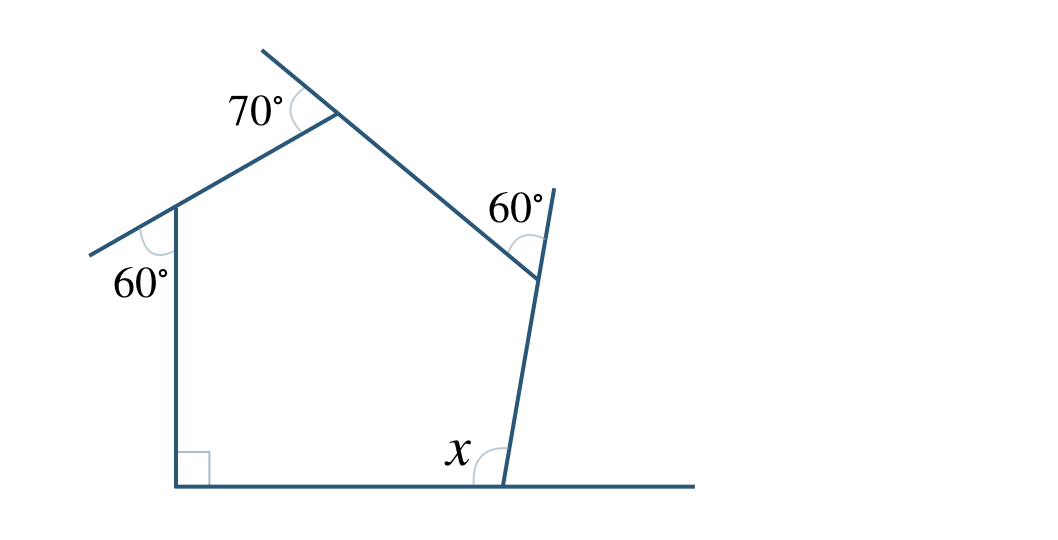
②
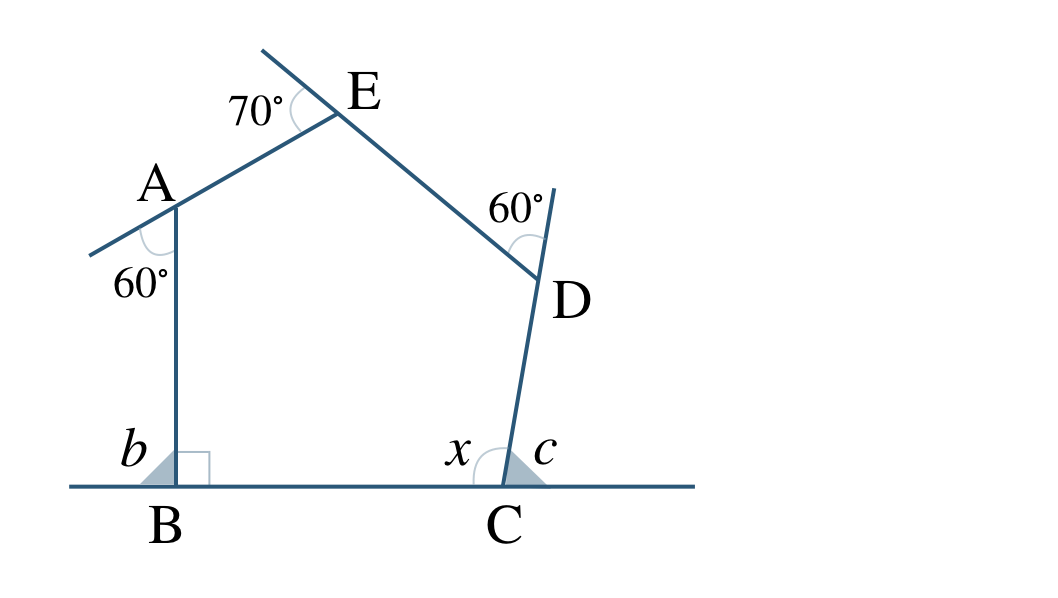
頂点 \({\rm B}\) における外角を \(\angle b\) とすると、内角が \(90^\circ\) より、
\(~~~\angle b=180^\circ-90^\circ=90^\circ\)
また、頂点 \({\rm C}\) における外角を \(\angle c\) とすると、外角の和が \(360^\circ\) より、
\(\begin{eqnarray}~60^\circ+90^\circ+\angle c+60^\circ+70^\circ&=&360^\circ\\[2pt]~~~\angle c+280^\circ&=&360^\circ\\[2pt]~~~\angle c&=&360^\circ-280^\circ\\[2pt]~~~\angle c&=&80^\circ\end{eqnarray}\)
\(\angle x\) は点 \({\rm C}\) の内角であるので、
\(\begin{eqnarray}~~~\angle x&=&180^\circ-\angle c\\[2pt]~~~&=&180^\circ-80^\circ\\[2pt]~~~&=&100^\circ\end{eqnarray}\)
したがって、答えは \(\angle x=100^\circ\) となる

【問題一覧】中2|合同な図形
このページは「中学数学2 合同な図形」の問題一覧ページとなります。解説の見たい単元名がわからないとき...


