問題:合同な図形の表し方
次の問いに答えよ。
\({\small (1)}~\)三角形 \({\rm ABC}\) と三角形 \({\rm DEF}\) が合同である。
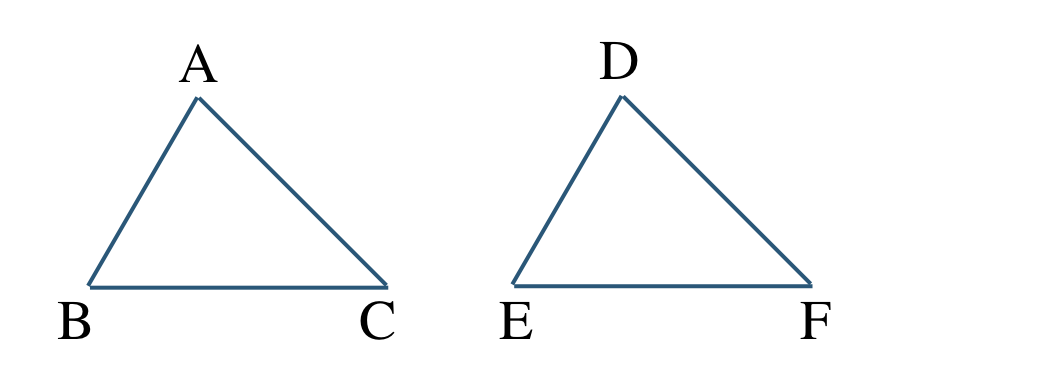
① 合同であることを記号で表せ。
② 等しい線分の長さを記号で表せ。
③ 等しい角の大きさを記号で表せ。
\({\small (2)}~\)次の2つの四角形は合同である。
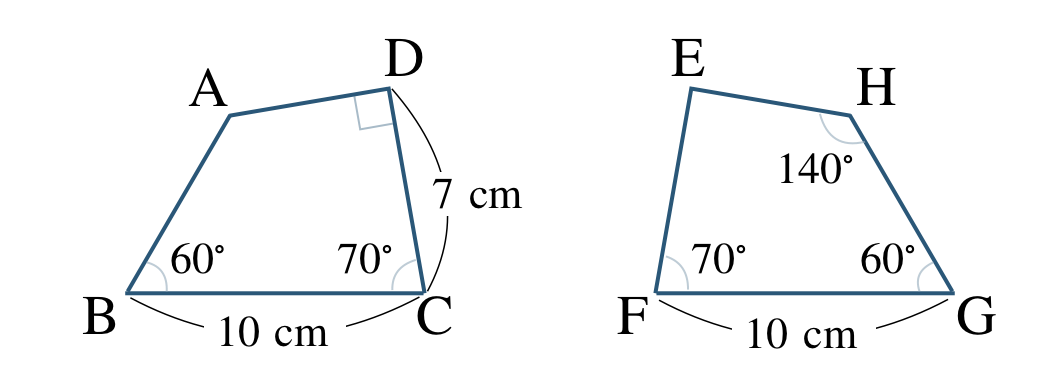
① 合同であることを記号で表せ。
② \(\angle {\rm A}\) の大きさを求めよ。
③ \(\angle {\rm E}\) の大きさを求めよ。
④ 線分 \({\rm EF}\) の長さを求めよ。
解法のPoint
2つの図形が合同であるとき、一方を移動して他方とぴったり重なる。
このとき、
重なり合う頂点を「対応する頂点」
重なり合う辺を「対応する辺」
重なり合う角を「対応する角」 という。
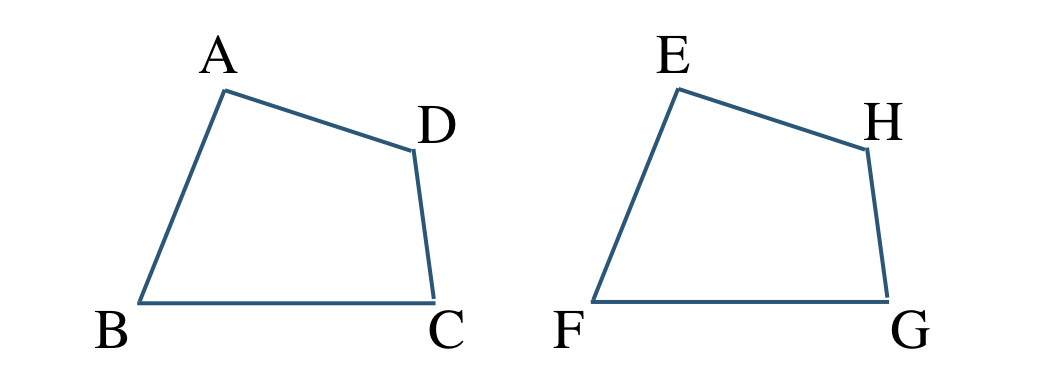
合同であることを記号 \(\equiv\) (合同と読む)を使って、
四角形 \({\rm ABCD}\) \(\equiv\) 四角形 \({\rm EFGH}\)
と表す。
また、合同な図形では、
対応する線分の長さはそれぞれ等しい
→ \({\rm AB=EF}\) など
対応する角の大きさはそれぞれ等しい
→ \({\rm \angle A=\angle E}\) など
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:合同な図形の表し方
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)三角形 \({\rm ABC}\) と三角形 \({\rm DEF}\) が合同である。

① 合同であることを記号で表せ。
② 等しい線分の長さを記号で表せ。
③ 等しい角の大きさを記号で表せ。
① 対応する頂点は、
\({\rm A}\) と \({\rm D}\)、\({\rm B}\) と \({\rm E}\)、\({\rm C}\) と \({\rm F}\)
であるので、
\(\triangle {\rm ABC}\equiv \triangle {\rm DEF}\)
となる
② 対応する線分の長さが等しいので、
\({\rm AB=DE~,~BC=EF~,~AC=DF}\)
となる
③ 対応する角の大きさが等しいので、
\({\rm \angle A=\angle D~,~\angle B=\angle E~,~\angle C=\angle F}\)
となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の2つの四角形は合同である。

① 合同であることを記号で表せ。
② \(\angle {\rm A}\) の大きさを求めよ。
③ \(\angle {\rm E}\) の大きさを求めよ。
④ 線分 \({\rm EF}\) の長さを求めよ。
① \({\rm BC=FG}=10~{\rm cm}\)、\({\rm \angle B=\angle G}=60^\circ\)、\({\rm \angle C=\angle F}=70^\circ\) であるので、
向きをそろえて図をかくと、
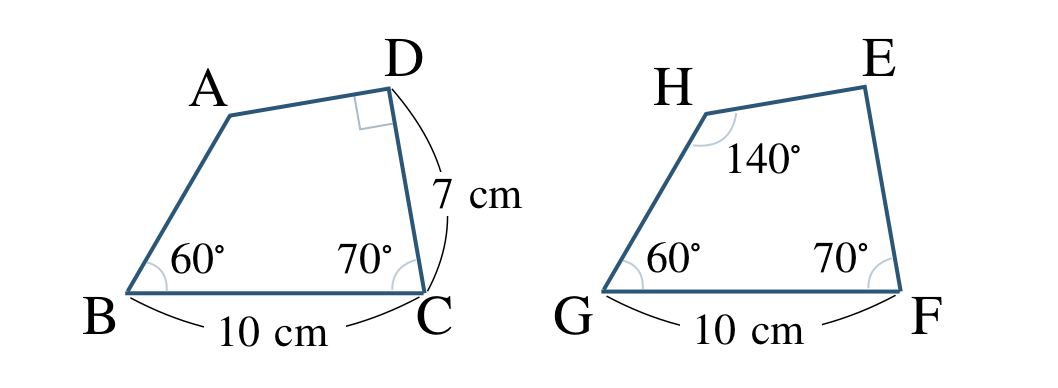
これより、対応する頂点は、
\({\rm A}\) と \({\rm H}\)、\({\rm B}\) と \({\rm G}\)、\({\rm C}\) と \({\rm F}\)、\({\rm D}\) と \({\rm E}\)
であるので、
四角形 \( {\rm ABCD}\equiv\) 四角形 \({\rm HGFE}\)
となる
② \(\angle {\rm A}\) に対応する角は \(\angle {\rm H}\) であるので、
\(\angle {\rm H}=140^\circ\) より、
\(\angle {\rm A}=140^\circ\)
となる
③ \(\angle {\rm E}\) に対応する角は \(\angle {\rm D}\) であるので、
\(\angle {\rm D}=90^\circ\) より、
\(\angle {\rm E}=90^\circ\)
となる
④ 線分 \({\rm EF}\) に対応する線分は、線分 \({\rm DC}\) であるので、
\({\rm DC}=7~{\rm cm}\) より、
\({\rm EF}=7~{\rm cm}\)
となる



