三角形の合同条件の解法
2つの三角形は次のどれかが成り立つとき、
合同 \(\triangle {\rm ABC}\equiv \triangle {\rm A’B’C’}\) である。
① 3組の辺がそれぞれ等しい。
\({\rm AB=A’B’~,~BC=B’C’~,~CA=C’A’}\)
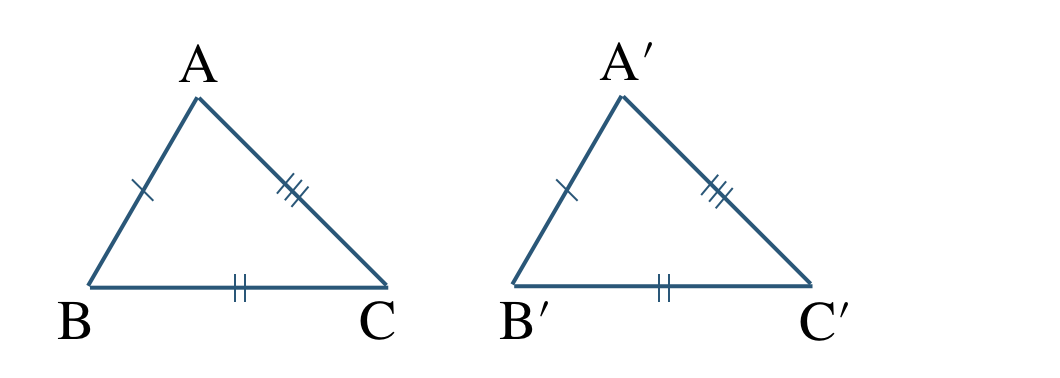
② 2組の辺とその間の角がそれぞれ等しい。
\({\rm AB=A’B’~,~BC=B’C’~,~\angle B=\angle B’}\)
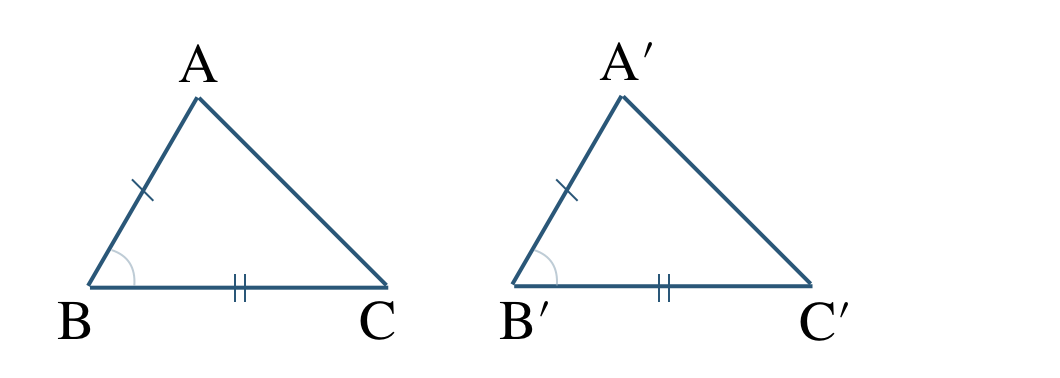
③ 1組の辺とその両端の角がそれぞれ等しい。
\({\rm BC=B’C’~,~\angle B=\angle B’~,~\angle C=\angle C’}\)

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:三角形の合同条件
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の図において、合同な図形を見つけて記号 \(\equiv\) で表し、合同条件を答えよ。
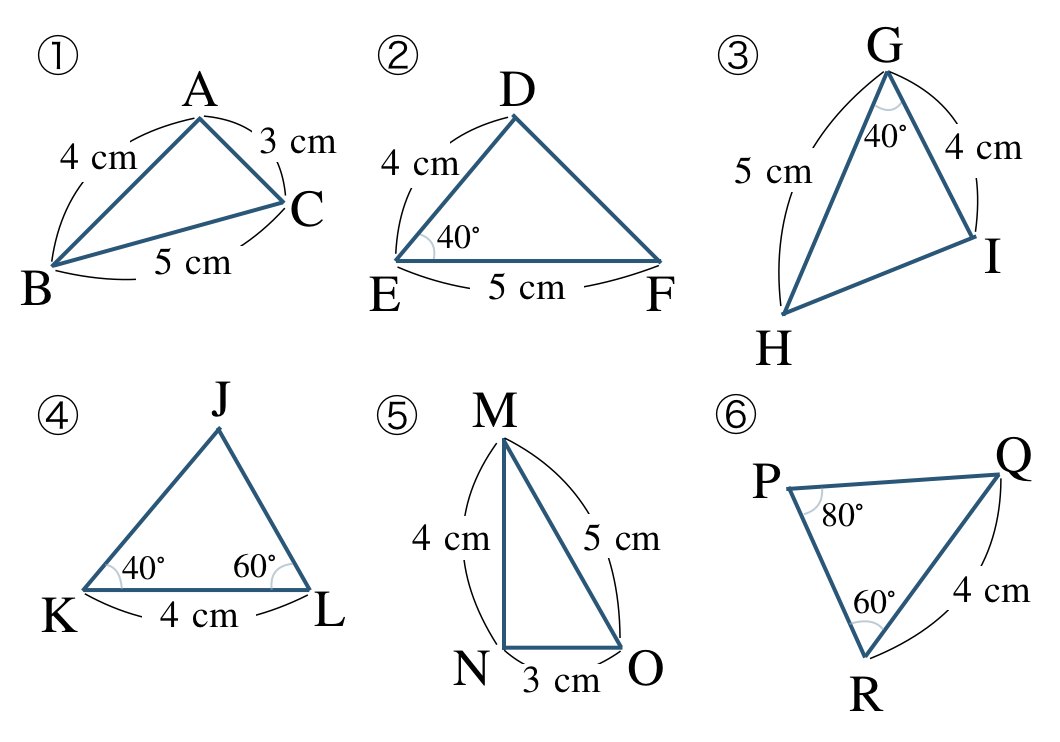
①と⑤において、
\({\rm AB=NM=4~cm~,~BC=MO=5~cm}\)
\({\rm AC=NO=3~cm}\)
①と⑤の向きをそろえると、
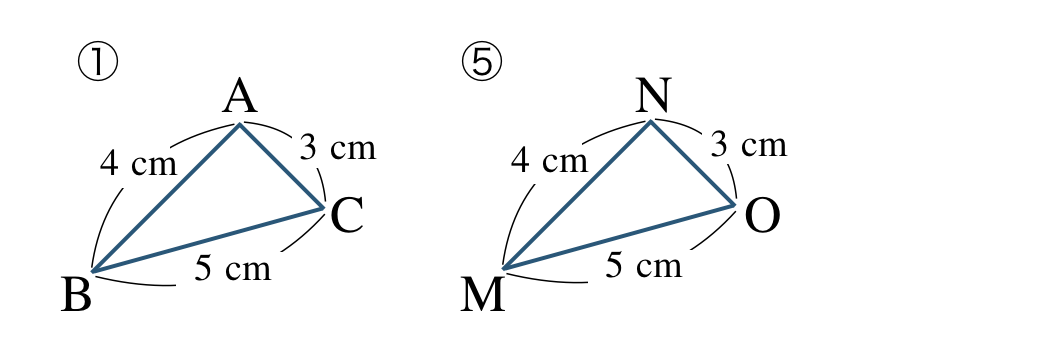
対応する頂点は、
\({\rm A}\) と \({\rm N}\)、\({\rm B}\) と \({\rm M}\)、\({\rm C}\) と \({\rm O}\)
であるので、
\(\triangle {\rm ABC}\equiv \triangle {\rm NMO}\)
合同条件は、
3組の辺がそれぞれ等しい
となる
②と③において、
\({\rm DE=IG=4~cm~,~EF=GH=5~cm}\)
\({\rm \angle E=\angle G=40^\circ}\)
②と③の向きをそろえると、
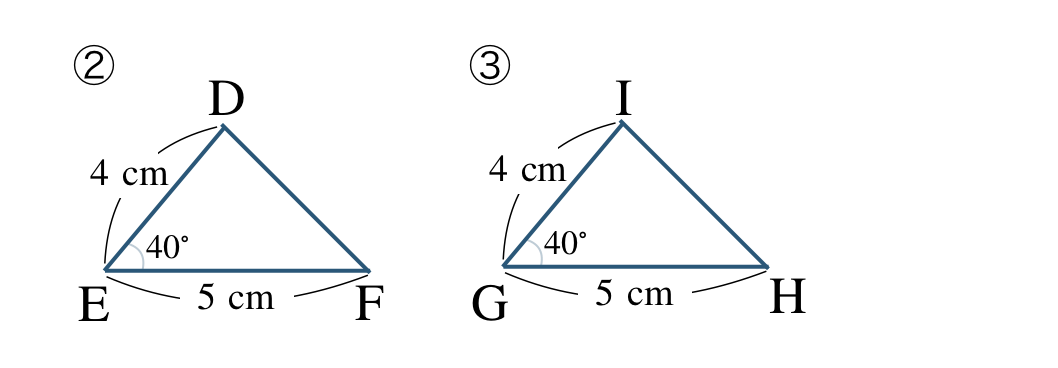
対応する頂点は、
\({\rm D}\) と \({\rm I}\)、\({\rm E}\) と \({\rm G}\)、\({\rm F}\) と \({\rm H}\)
であるので、
\(\triangle {\rm DEF}\equiv \triangle {\rm IGH}\)
合同条件は、
2組の辺とその間の角がそれぞれ等しい
となる
⑥について、$$\begin{eqnarray}~~~{\rm \angle Q}&=&180^\circ-({\rm \angle P+\angle Q})\\[2pt]~~~&=&180^\circ-(60^\circ+80^\circ)\\[2pt]~~~&=&40^\circ\end{eqnarray}$$④と⑥において、
\({\rm KL=QR=4~cm~,~\angle K=\angle Q=40^\circ}\)
\({\rm \angle L=\angle R=60^\circ}\)
④と⑥の向きをそろえると、
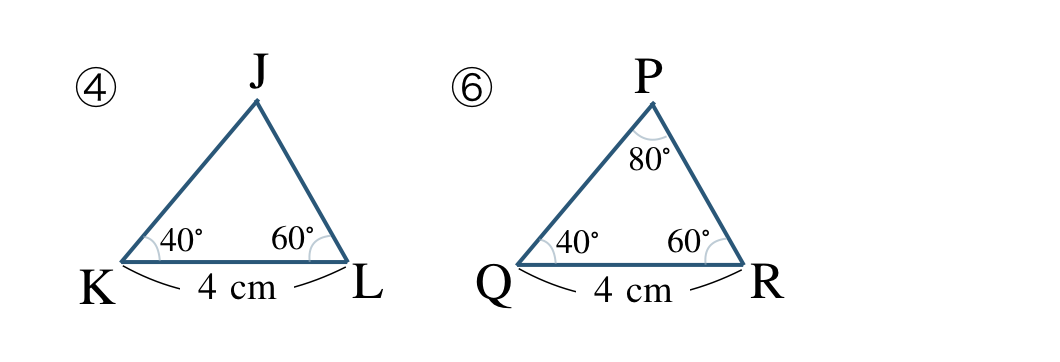
対応する頂点は、
\({\rm J}\) と \({\rm P}\)、\({\rm K}\) と \({\rm Q}\)、\({\rm L}\) と \({\rm R}\)
であるので、
\(\triangle {\rm JKL}\equiv \triangle {\rm PQR}\)
合同条件は、
1組の辺とその両端の角がそれぞれ等しい
となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の図において、合同な三角形を見つけて記号 \(\equiv\) で表し、合同条件を答えよ。ただし、それぞれの図形で同じ記号のついた辺や角は等しいとする。
①
②
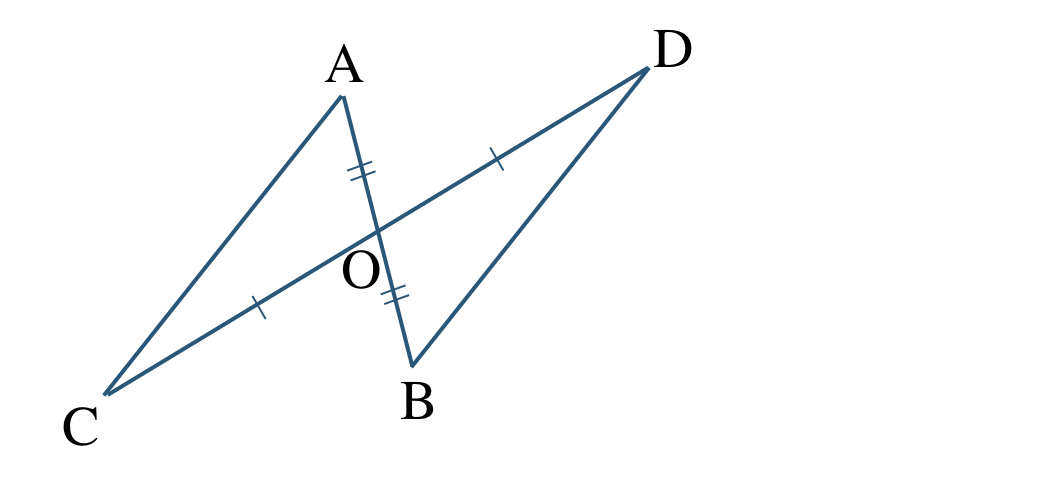
③
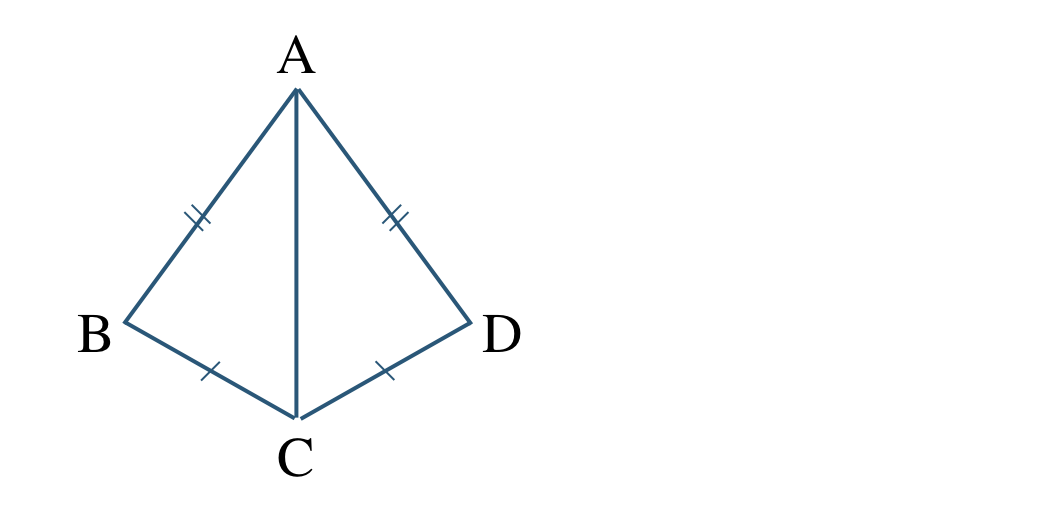
① \(\triangle {\rm ABC}\) と \(\triangle {\rm ADC}\) において、
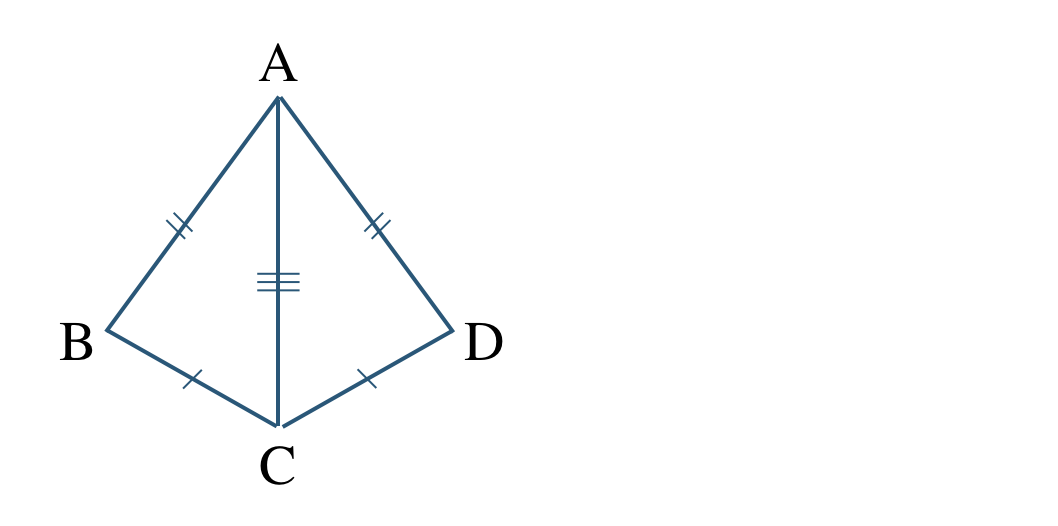
\({\rm AC=AC}\) (共通の辺)
対称移動で向きをそろえると、
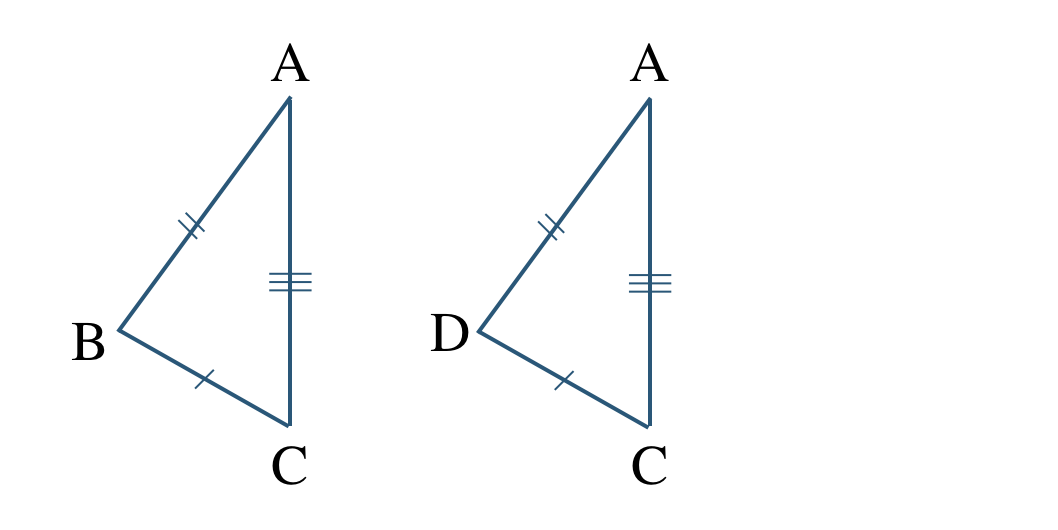
対応する頂点は、
\({\rm A}\) と \({\rm A}\)、\({\rm B}\) と \({\rm D}\)、\({\rm C}\) と \({\rm C}\)
であるので、
\(\triangle {\rm ABC}\equiv \triangle {\rm ADC}\)
合同条件は、
3組の辺がそれぞれ等しい
となる
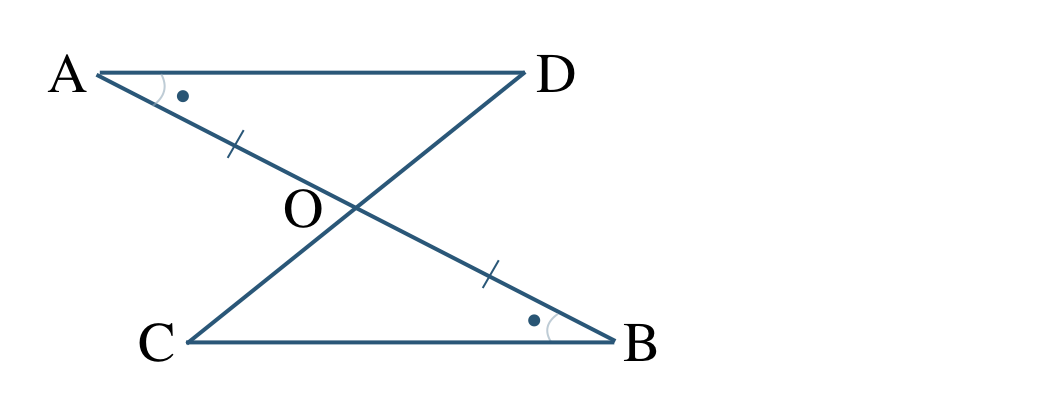
② \(\triangle {\rm AOC}\) と \(\triangle {\rm BOD}\) において、

\({\rm \angle AOC=\angle BOD}\) (対頂角)
回転移動で向きをそろえると、
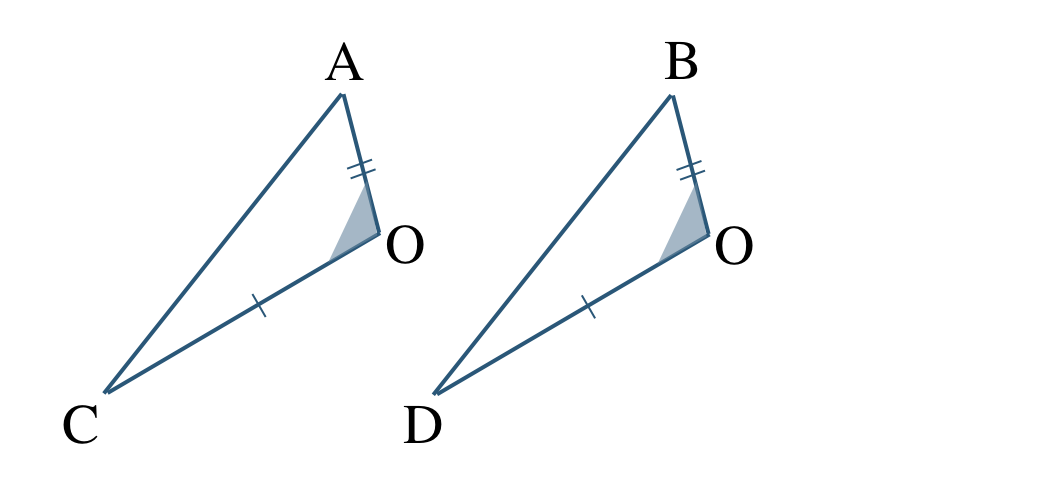
対応する頂点は、
\({\rm A}\) と \({\rm B}\)、\({\rm O}\) と \({\rm O}\)、\({\rm C}\) と \({\rm D}\)
であるので、
\(\triangle {\rm AOC}\equiv \triangle {\rm BOD}\)
合同条件は、
2組の辺とその間の角がそれぞれ等しい
となる
③ \(\triangle {\rm AOD}\) と \(\triangle {\rm BOC}\) において、
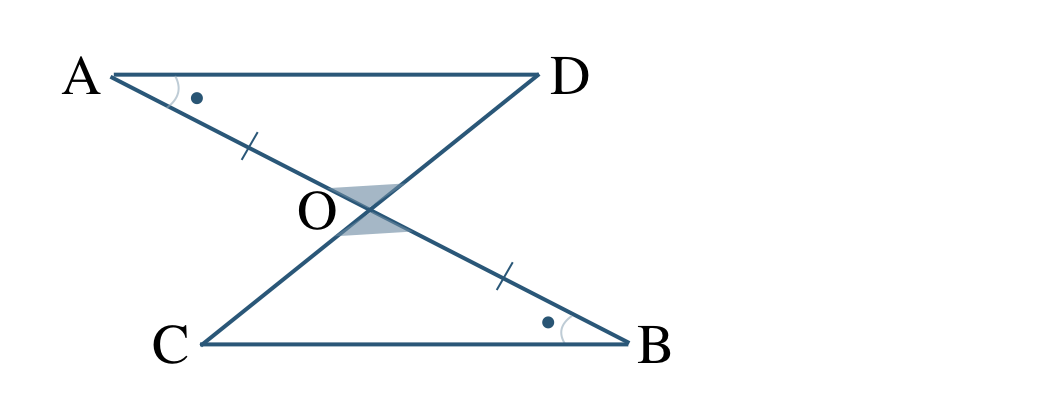
\({\rm \angle AOD=\angle BOC}\) (対頂角)
回転移動で向きをそろえると、
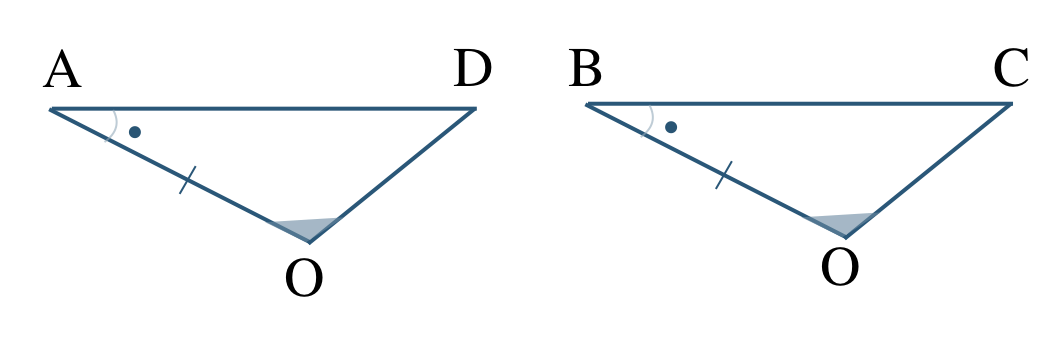
対応する頂点は、
\({\rm A}\) と \({\rm B}\)、\({\rm O}\) と \({\rm O}\)、\({\rm D}\) と \({\rm C}\)
であるので、
\(\triangle {\rm AOD}\equiv \triangle {\rm BOC}\)
合同条件は、
1組の辺とその両端の角がそれぞれ等しい
となる



