問題:展開・因数分解と図形の性質
問題
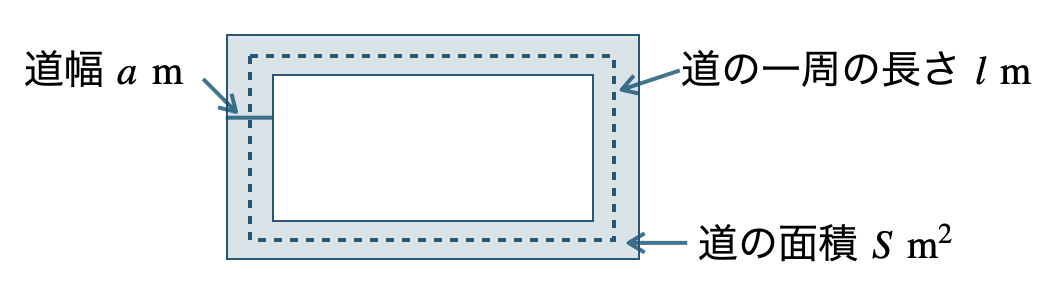
次の図のように、長方形の土地のまわりに幅 \(a~{\rm m}\) の道がある。この道の真ん中を通る線の一周の長さ \(l~{\rm m}\) で道の面積が \(S~{\rm m}^2\) である。
このとき、\(S=al\) が成り立つことを証明せよ。

解法のPoint
Point:道の長さと面積の関係
道幅 \(a~{\rm m}\) 、道の真ん中を通る線の一周の長さ \(l~{\rm m}\) 、道の面積 \(S~{\rm m}^2\) であるとき、
\(S=al\)
これを証明する手順は、
① 内側の土地の縦の長さを \(x~{\rm m}\) 、横の長さを \(y~{\rm m}\) とする。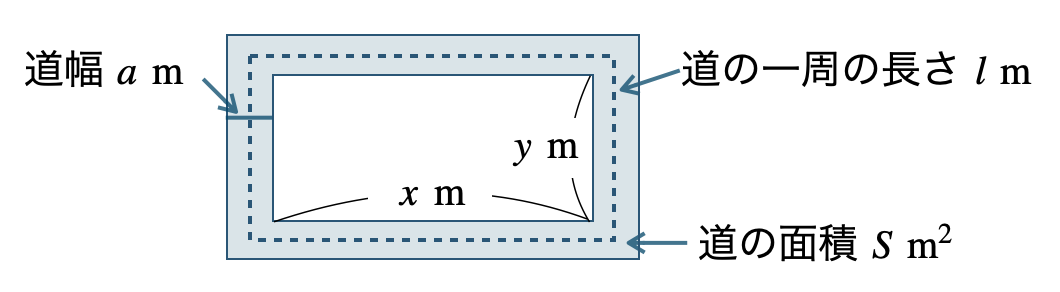
③ 道の真ん中を通る線の一周の長さ \(l~{\rm m}\) を道幅の半分の長さ \(\begin{split}{\frac{\,a\,}{\,2\,}}~{\rm m}\end{split}\) を用いて求める。
④ ②と③の式を比較して、\(S=al\) となることを証明する。
■ 道の長さと面積の関係
道幅 \(a~{\rm m}\) 、道の真ん中を通る線の一周の長さ \(l~{\rm m}\) 、道の面積 \(S~{\rm m}^2\) であるとき、
\(S=al\)
これを証明する手順は、
① 内側の土地の縦の長さを \(x~{\rm m}\) 、横の長さを \(y~{\rm m}\) とする。

② 道の面積 \(S~{\rm m}^2\) を「全体の面積ー内側の土地の面積」から求める。
③ 道の真ん中を通る線の一周の長さ \(l~{\rm m}\) を道幅の半分の長さ \(\begin{split}{\frac{\,a\,}{\,2\,}}~{\rm m}\end{split}\) を用いて求める。
④ ②と③の式を比較して、\(S=al\) となることを証明する。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:展開・因数分解と図形の性質
問題解説
問題

次の図のように、長方形の土地のまわりに幅 \(a~{\rm m}\) の道がある。この道の真ん中を通る線の一周の長さ \(l~{\rm m}\) で道の面積が \(S~{\rm m}^2\) である。
このとき、\(S=al\) が成り立つことを証明せよ。

[証明] 内側の土地の縦の長さを \(x~{\rm m}\) 、横の長さを \(y~{\rm m}\) とすると、
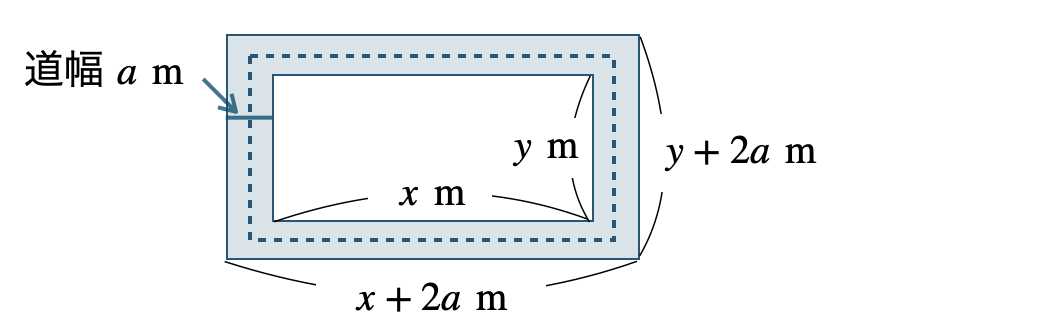
全体の縦の長さが、\(x+a+a=x+2a~[\,{\rm m}\,]\)
横の長さが、\(y+a+a=y+2a~[\,{\rm m}\,]\)
となるので、全体の面積は、
\(\begin{split}&(x+2a)(y+2a)
\\[2pt]~~=~&x{\, \small \times \,} y+x{\, \small \times \,} 2a+2a{\, \small \times \,} y+2a{\, \small \times \,} 2a\\[2pt]~~=~&xy+2ax+2ay+4a^2~[\,{\rm m^2}\,]\end{split}\)
また、内側の面積は、\(x{\, \small \times \,} y=xy~[\,{\rm m^2}\,]\)
である
よって、
道の面積 \(S~{\rm m}^2\) は全体の面積ー内側の土地の面積より、
\(\begin{eqnarray}~~~S&=&(xy+2ax+2ay+4a^2)-xy\\[2pt]~~~&=&(xy-xy)+2ax+2ay+4a^2\\[2pt]~~~&=&2ax+2ay+4a^2\\[2pt]~~~&=&a{\, \small \times \,} 2x+a{\, \small \times \,} 2y +a{\, \small \times \,} 4a\\[2pt]~~~&=&a(2x+2y+4a)~[\,{\rm m^2}\,]\end{eqnarray}\)
次に、道の真ん中を通る線の一周の長さ \(l~{\rm m}\) は、
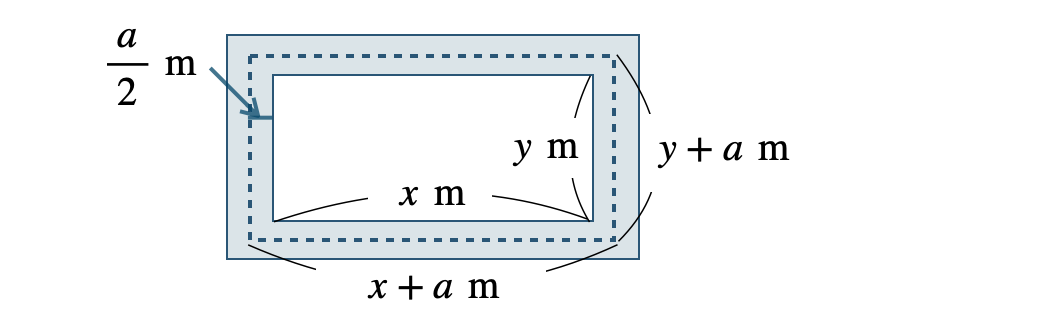
縦の長さが、
\(\begin{split}&x+\frac{\,a \,}{\,2 \,}+\frac{\,a \,}{\,2 \,}\\[3pt]~~=~&x+\frac{\,a+a \,}{\,2 \,}=x+\frac{\,2a \,}{\,2 \,}=x+a~[\,{\rm m}\,]\end{split}\)
横の長さが、
\(\begin{split}&y+\frac{\,a \,}{\,2 \,}+\frac{\,a \,}{\,2 \,}\\[3pt]~~=~&y+\frac{\,a+a \,}{\,2 \,}=y+\frac{\,2a \,}{\,2 \,}=y+a~[\,{\rm m}\,]\end{split}\)
一周の長さは、縦の長さ×2+横の長さ×2より、
\(\begin{eqnarray}~~~l&=&2(x+a)+2(y+a)\\[2pt]~~~&=&2x+2a+2y+2a\\[2pt]~~~&=&2x+2y+(2a+2a)\\[2pt]~~~&=&2x+2y+4a~[\,{\rm m}\,]\end{eqnarray}\)
したがって、
\(~~~~~S=a(2x+2y+4a)\)
\(~~~~~l=2x+2y+4a\)
であるので、\(S=al\)が成り立つ。[終]

【問題一覧】中3|展開と因数分解
このページは「中学数学3 展開と因数分解」の問題一覧ページとなります。解説の見たい単元名がわからない...


