問題:関数y=ax²と図形
下の図のように、直角二等辺三角形 \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が直線 \(l\) 上に並んでいて、点 \({\rm C}\) と点 \({\rm Q}\) が重なっている。
\(\triangle {\rm ABC}\) が直線 \(l\) にそって右方向に毎秒 \(1~{\rm cm}\) の速さで点 \({\rm C}\) が点 \({\rm R}\) と重なるまで動く。
\(\triangle {\rm ABC}\) が動きはじめて \(x\) 秒後の \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が重なってできる部分の面積を \(y~{\rm cm}^2\) とする。
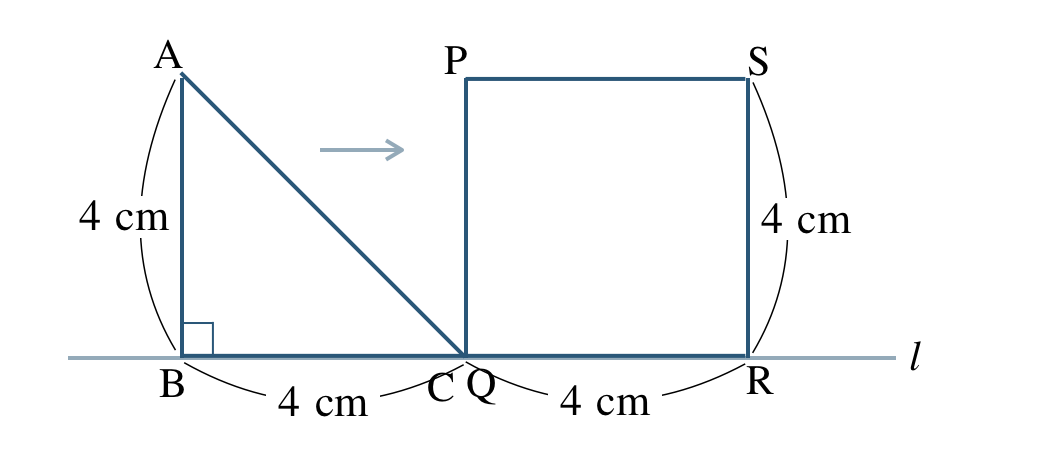
\({\small (1)}~\)\(y\) を \(x\) の式で表して、\(x\) の変域を答えよ。
\({\small (2)}~\)\(x\) と \(y\) の関係をクラブで表せ。
\({\small (3)}~\)\(3\) 秒後の重なって部分の面積 \({\rm cm}^2\) を求めよ。
\({\small (4)}~\)重なって部分の面積 \(4~{\rm cm}^2\) となるのは何秒後が答えよ。
解法のPoint
図のように、2つの直角二等辺三角形があり、\(\triangle {\rm ABC}\) が毎秒 \(1~{\rm cm}\) の速さで右にぴったりと重なるまで移動する。
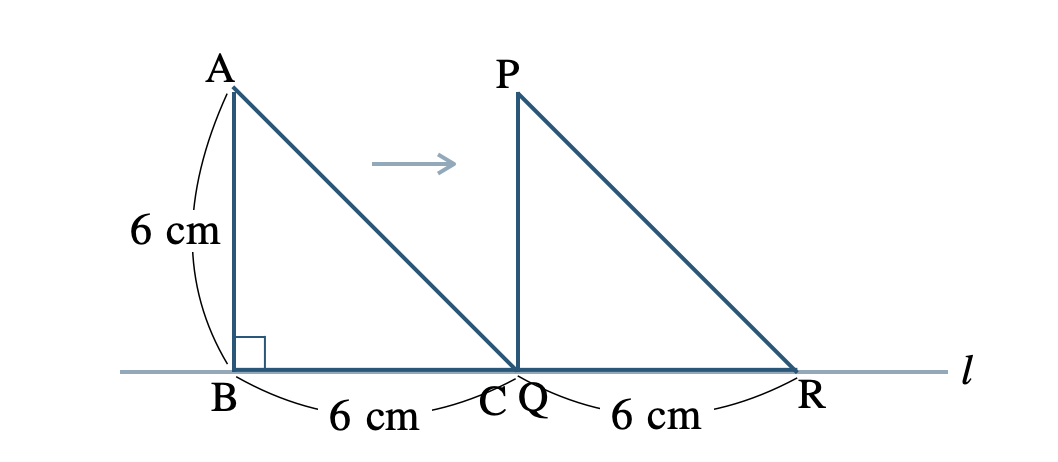
① \(x\) 秒後の図でかく。
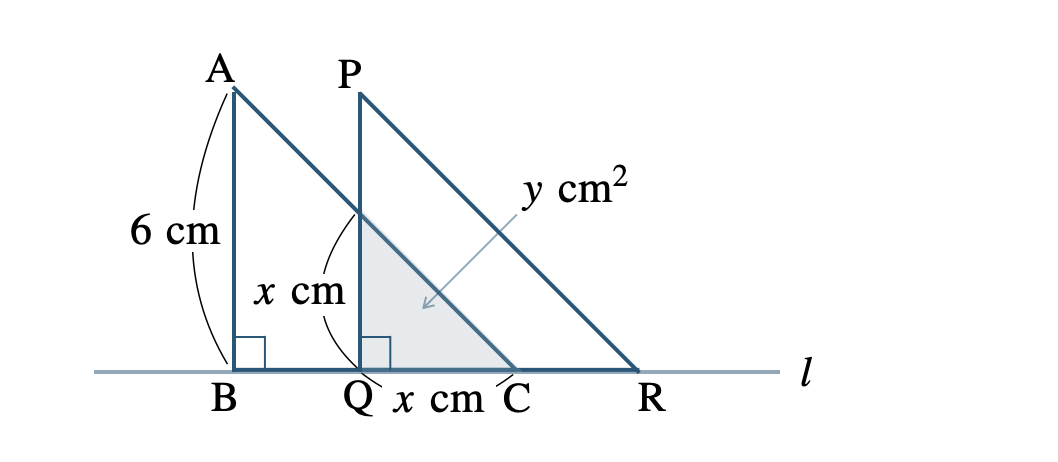
② 重なった部分も直角二等辺三角形となることより、面積 \(y~{\rm cm}^2\) を求める。
高さも \(x~{\rm cm}\) となるので、\(\begin{split}y=\frac{\,1\,}{\,2\,}x^2\end{split}\)
③ \(x\) の変域を求める。
重なるまで \(x=6\) 秒かかるので、
\(x\) の変域は、\(0≦x≦6\) となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:関数y=ax²と図形
問題解説(1)
下の図のように、直角二等辺三角形 \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が直線 \(l\) 上に並んでいて、点 \({\rm C}\) と点 \({\rm Q}\) が重なっている。
\(\triangle {\rm ABC}\) が直線 \(l\) にそって右方向に毎秒 \(1~{\rm cm}\) の速さで点 \({\rm C}\) が点 \({\rm R}\) と重なるまで動く。
\(\triangle {\rm ABC}\) が動きはじめて \(x\) 秒後の \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が重なってできる部分の面積を \(y~{\rm cm}^2\) とする。

\({\small (1)}~\)\(y\) を \(x\) の式で表して、\(x\) の変域を答えよ。
\(x\) 秒後の直角二等辺三角形 \(\triangle {\rm ABC}\) は、
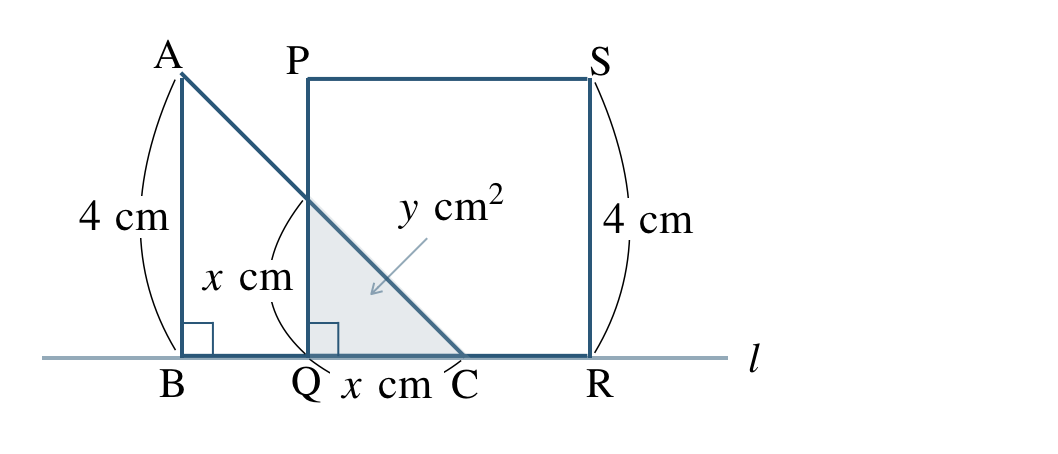
重なった部分も直角二等辺三角形となるので、高さも \(x~{\rm cm}\) となる
よって、面積 \(y~{\rm cm}^2\) は、
\(\begin{eqnarray}~~~y&=&x{\, \small \times \,} x{\, \small \times \,} \frac{\,1\,}{\,2\,}\\[3pt]~~~&=&\frac{\,1\,}{\,2\,}x^2\end{eqnarray}\)
また、点 \({\rm C}\) と点 \({\rm R}\) が重なるまで移動するので、\(4~{\rm cm}\) 動き \(4\) 秒かかる
よって、\(x\) の変域は、\(\begin{split}0≦x≦4\end{split}\) となる
したがって、\(\begin{split}y=\frac{\,1\,}{\,2\,}x^2~~(0≦x≦4)\end{split}\) となる
問題解説(2)
下の図のように、直角二等辺三角形 \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が直線 \(l\) 上に並んでいて、点 \({\rm C}\) と点 \({\rm Q}\) が重なっている。
\(\triangle {\rm ABC}\) が直線 \(l\) にそって右方向に毎秒 \(1~{\rm cm}\) の速さで点 \({\rm C}\) が点 \({\rm R}\) と重なるまで動く。
\(\triangle {\rm ABC}\) が動きはじめて \(x\) 秒後の \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が重なってできる部分の面積を \(y~{\rm cm}^2\) とする。

\({\small (2)}~\)\(x\) と \(y\) の関係をクラブで表せ。
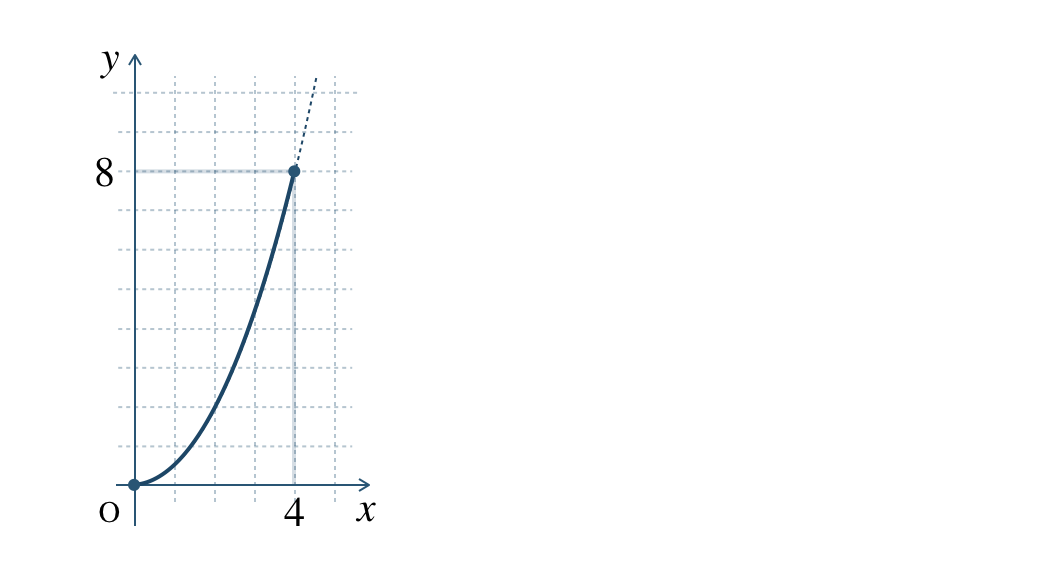
\(x\) と \(y\) の関係の式は、\(\begin{split}y=\frac{\,1\,}{\,2\,}x^2~~(0≦x≦4)\end{split}\)
これより、グラフは、
問題解説(3)
下の図のように、直角二等辺三角形 \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が直線 \(l\) 上に並んでいて、点 \({\rm C}\) と点 \({\rm Q}\) が重なっている。
\(\triangle {\rm ABC}\) が直線 \(l\) にそって右方向に毎秒 \(1~{\rm cm}\) の速さで点 \({\rm C}\) が点 \({\rm R}\) と重なるまで動く。
\(\triangle {\rm ABC}\) が動きはじめて \(x\) 秒後の \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が重なってできる部分の面積を \(y~{\rm cm}^2\) とする。

\({\small (3)}~\)\(3\) 秒後の重なって部分の面積 \({\rm cm}^2\) を求めよ。
\(3\) 秒後より、
\(x=3\) を \(\begin{split}y={\frac{\,1\,}{\,2\,}}x^2\end{split}\) に代入すると、
\(\begin{eqnarray}~~~y&=&\frac{\,1\,}{\,2\,}{\, \small \times \,} 3^2\\[3pt]~~~&=&\frac{\,1\,}{\,2\,}{\, \small \times \,}9\\[3pt]~~~&=&\frac{\,9\,}{\,2\,}\end{eqnarray}\)
したがって、面積 \(\begin{split}{\frac{\,9\,}{\,2\,}}~{\rm cm}^2\end{split}\) となる
問題解説(4)
下の図のように、直角二等辺三角形 \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が直線 \(l\) 上に並んでいて、点 \({\rm C}\) と点 \({\rm Q}\) が重なっている。
\(\triangle {\rm ABC}\) が直線 \(l\) にそって右方向に毎秒 \(1~{\rm cm}\) の速さで点 \({\rm C}\) が点 \({\rm R}\) と重なるまで動く。
\(\triangle {\rm ABC}\) が動きはじめて \(x\) 秒後の \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が重なってできる部分の面積を \(y~{\rm cm}^2\) とする。

\({\small (4)}~\)重なって部分の面積 \(4~{\rm cm}^2\) となるのは何秒後が答えよ。
面積 \(4~{\rm cm}^2\) より、
\(y=4\) を \(\begin{split}y={\frac{\,1\,}{\,2\,}}x^2\end{split}\) に代入すると、
\(\begin{split}\hspace{50pt}~~~4=\frac{\,1\,}{\,2\,}x^2\end{split}\)
両辺を入れかえて、両辺に \(2\) をかけると、
\(\require{cancel} \begin{eqnarray}~~~\frac{\,1\,}{\,2\,}x^2&=&4\\[3pt]~~~\frac{\,1\,}{\,2\,}x^2{\, \small \times \,}2&=&4{\, \small \times \,}2\\[3pt]~~~\frac{\,1\,}{\,\cancel{2}^{1}\,}x^2{\, \small \times \,}\cancel{2}^{1}&=&8\\[3pt]~~~x^2&=&8\\[2pt]~~~x&=&\pm\sqrt{8}\\[2pt]~~~x&=&\pm2\sqrt{2}\end{eqnarray}\)
\(0≦x≦4\) であるので、\(x=2\sqrt{2}\) となる
したがって、\(2\sqrt{2}\) 秒後となる



