問題:放物線と直線
関数 \(y=x^2\) のグラフが直線 \(l\) と2点 \({\rm A~,~B}\) で交わる。2点 \({\rm A~,~B}\) の \(x\) 座標がそれぞれ \(-2~,~3\) であるとき、次の問いに答えよ。
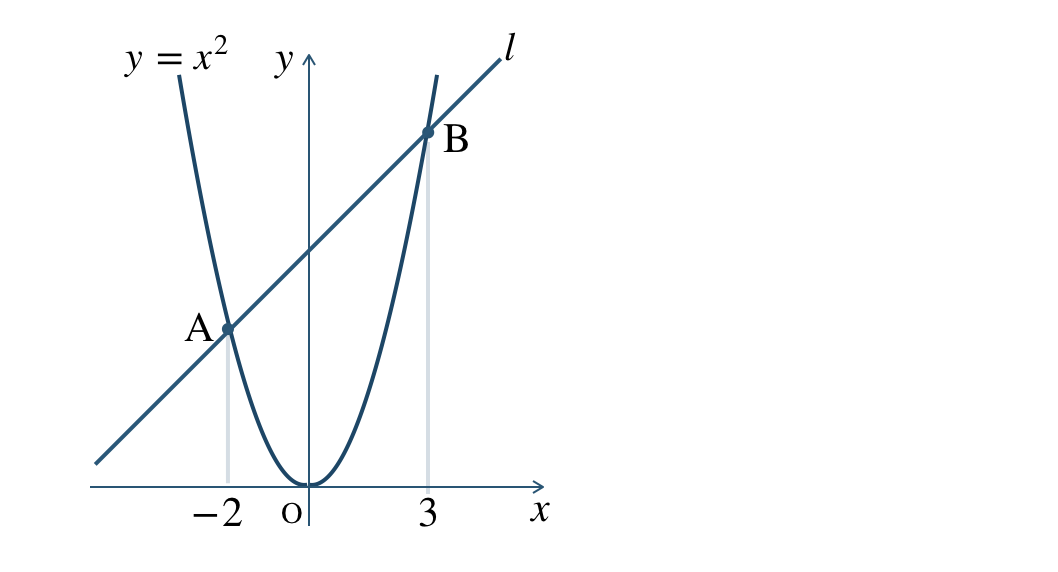
\({\small (1)}~\)2点 \({\rm A~,~B}\) の座標を求めよ。
\({\small (2)}~\)直線 \(l\) の式を求めよ。
\({\small (3)}~\)\(\triangle {\rm OAB}\) の面積を求めよ。
解法のPoint
放物線 \(y=x^2\) と直線との交点 \({\rm A~,~B}\) の \(x\) 座標が \(2~,~-1\) のとき、\(\triangle {\rm OAB}\) の面積は、
① 交点の \(x\) 座標を放物線に代入して、\(y\) 座標を求める。
\(x=2\) のとき、\(y=2^2=4\)
\(x=-1\) のとき、\(y=(-1)^2=1\)
② 2点 \({\rm A~,~B}\) を結んだ直線の式を求める。
2点 \({\rm A}(2~,~4)~,~{\rm B}(-1~,~1)\) より、
直線の式は、\(y=x+2\)
③ 直線の切片を底辺と考えて、\(\triangle {\rm OAB}\) を2つの三角形に分けて面積を求める。
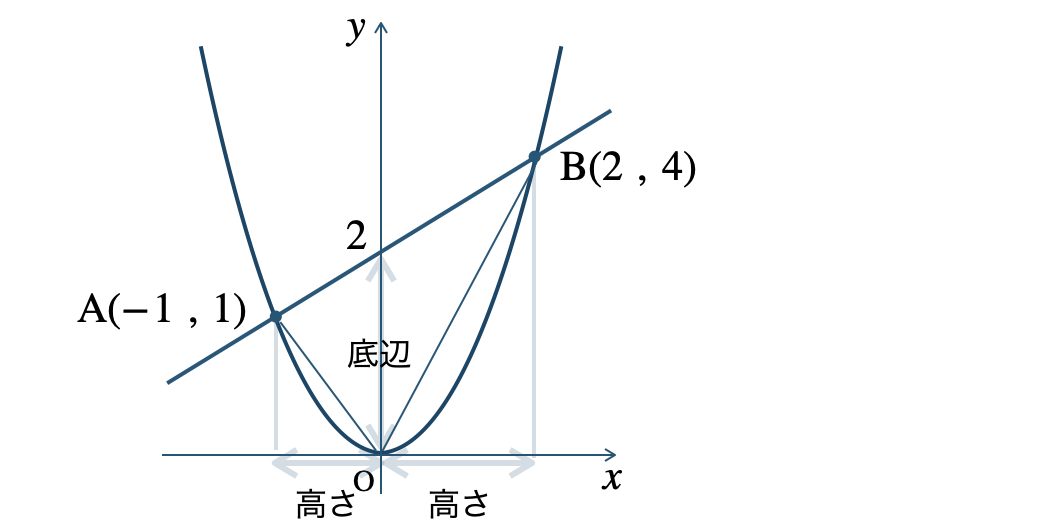
\(\begin{split}\triangle {\rm OAB}=\frac{\,1\,}{\,2\,}{\, \small \times \,}2{\, \small \times \,}1+\frac{\,1\,}{\,2\,}{\, \small \times \,}2{\, \small \times \,}2=3\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:放物線と直線
問題解説(1)
関数 \(y=x^2\) のグラフが直線 \(l\) と2点 \({\rm A~,~B}\) で交わる。2点 \({\rm A~,~B}\) の \(x\) 座標がそれぞれ \(-2~,~3\) であるとき、次の問いに答えよ。

\({\small (1)}~\)2点 \({\rm A~,~B}\) の座標を求めよ。
点 \({\rm A~,~B}\) は関数 \(y=x^2\) 上の点より、
点 \({\rm A}\) の \(x\) 座標が \(-2\) より、
\(\begin{split}~~~y=(-2)^2=4\end{split}\)
点 \({\rm B}\) の \(x\) 座標が \(3\) より、
\(\begin{split}~~~y=3^2=9\end{split}\)
したがって、\(\begin{split}{\rm A}(-2~,~4)~,~{\rm B}(3~,~9)\end{split}\) となる
問題解説(2)
関数 \(y=x^2\) のグラフが直線 \(l\) と2点 \({\rm A~,~B}\) で交わる。2点 \({\rm A~,~B}\) の \(x\) 座標がそれぞれ \(-2~,~3\) であるとき、次の問いに答えよ。

\({\small (2)}~\)直線 \(l\) の式を求めよ。
2点 \((-2~,~4)~,~(3~,~9)\) より、
この直線の傾き \(a\) は、
\(x\) の増加量 \(3-(-2)=3+2=5\)
\(y\) の増加量 \(9-4=5\)
これより、
\(\begin{split}~~~a=\frac{\,9-4\,}{\,3-(-2)\,}=\frac{\,5\,}{\,5\,}=1\end{split}\)
よって、\(y=x+b\) となる
これに点 \((-2~,~4)\) を代入すると、
(※ 点 \((-2~,~4)\) を代入してもよい。)
\(\begin{eqnarray}~~~4&=&-2+b\\[2pt]~~~-2+b&=&4\\[2pt]~~~b&=&4+2\\[2pt]~~~b&=&6\end{eqnarray}\)
したがって、直線の式 \(y=x+6\) となる
問題解説(3)
関数 \(y=x^2\) のグラフが直線 \(l\) と2点 \({\rm A~,~B}\) で交わる。2点 \({\rm A~,~B}\) の \(x\) 座標がそれぞれ \(-2~,~3\) であるとき、次の問いに答えよ。

\({\small (3)}~\)\(\triangle {\rm OAB}\) の面積を求めよ。
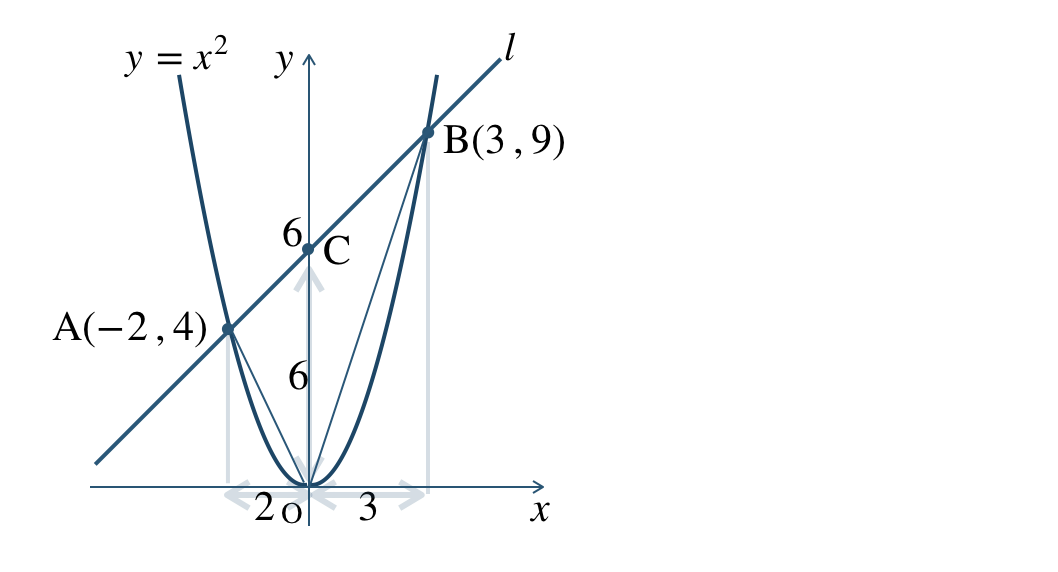
直線の切片を点 \({\rm C}\) とすると、
\(\triangle {\rm OAC}\) の面積は \({\rm OC}=6\) を底辺とすると、点 \({\rm A}\) の \(x\) 座標より高さが \(2\) となるので、
\(\begin{split}~~~\triangle {\rm OAC}=6{\, \small \times \,}2{\, \small \times \,}\frac{\,1\,}{\,2\,}=6\end{split}\)
また、\(\triangle {\rm OBC}\) の面積は \({\rm OC}=6\) を底辺とすると、点 \({\rm B}\) の \(x\) 座標より高さが \(3\) となるので、
\(\begin{split}~~~\triangle {\rm OBC}=6{\, \small \times \,}3{\, \small \times \,}\frac{\,1\,}{\,2\,}=9\end{split}\)
よって、\(\triangle {\rm OAB}\) の面積は、
\(\begin{split}~~~6+9=15\end{split}\)
したがって、面積は \(15\) となる



