問題:いろいろな関数
問題
\({\small (2)}~\)B社の通信量 \(x~{\rm GB}\) と料金 \(y\) 円の関係を表すグラフをかけ。
\({\small (3)}~\)次の通信量を使うとき、A社とB社のどちらか安いか答えよ。
① \(2~{\rm GB}\) ② \(4~{\rm GB}\)
③ \(6~{\rm GB}\) ④ \(8~{\rm GB}\)
次の表はA社とB社の通信量とその料金の表である。
| A社 | \(\small 5~{\rm GB}\) 以下 | \(\small 10~{\rm GB}\) 以下 |
| 料金 | \(800\) 円 | \(1600\) 円 |
| B社 | \(\small 3~{\rm GB}\) 以下 | \(\small 7~{\rm GB}\) 以下 | \(\small 10~{\rm GB}\) 以下 |
| 料金 | \(500\) 円 | \(1000\) 円 | \(1500\) 円 |
\({\small (1)}~\)A社の通信量 \(x~{\rm GB}\) と料金 \(y\) 円の関係を表すグラフをかけ。
\({\small (2)}~\)B社の通信量 \(x~{\rm GB}\) と料金 \(y\) 円の関係を表すグラフをかけ。
\({\small (3)}~\)次の通信量を使うとき、A社とB社のどちらか安いか答えよ。
① \(2~{\rm GB}\) ② \(4~{\rm GB}\)
③ \(6~{\rm GB}\) ④ \(8~{\rm GB}\)
解法のPoint
Point:いろいろな関数
これより、\(5~{\rm kg}\) の荷物の料金は \(500\) 円となる。
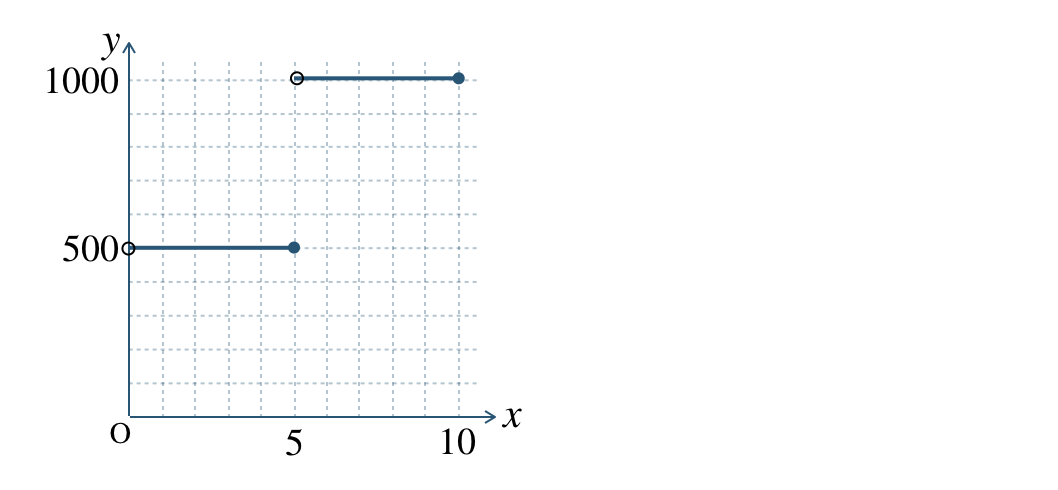
ある荷物を送るときの料金が、
\(5~{\rm kg}\) 以下では \(500\) 円
\(10~{\rm kg}\) 以下では \(1000\) 円
であるとき、荷物の重さ \(x~{\rm kg}\) の料金を \(y\) 円としたときのグラフは、

グラフの端の点をふくむときは●、ふくまないときは◯で表す。
これより、\(5~{\rm kg}\) の荷物の料金は \(500\) 円となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:いろいろな関数
問題解説(1)
問題
次の表はA社とB社の通信量とその料金の表である。
| A社 | \(\small 5~{\rm GB}\) 以下 | \(\small 10~{\rm GB}\) 以下 |
| 料金 | \(800\) 円 | \(1600\) 円 |
| B社 | \(\small 3~{\rm GB}\) 以下 | \(\small 7~{\rm GB}\) 以下 | \(\small 10~{\rm GB}\) 以下 |
| 料金 | \(500\) 円 | \(1000\) 円 | \(1500\) 円 |
\({\small (1)}~\)A社の通信量 \(x~{\rm GB}\) と料金 \(y\) 円の関係を表すグラフをかけ。
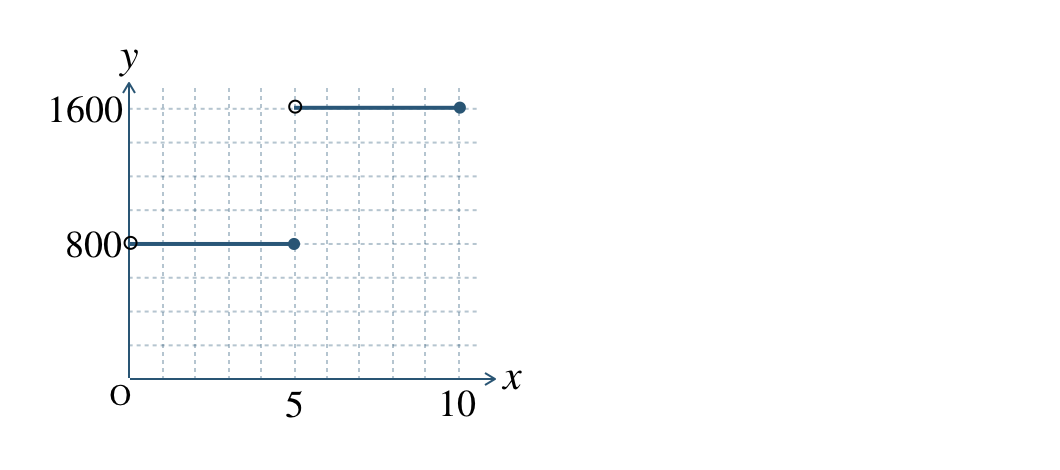
A社の表より、
\(0<x≦5\) のとき、\(y=800\)
\(5<x≦10\) のとき、\(y=1600\)
であるので、グラフは、
問題解説(2)
問題
次の表はA社とB社の通信量とその料金の表である。
| A社 | \(\small 5~{\rm GB}\) 以下 | \(\small 10~{\rm GB}\) 以下 |
| 料金 | \(800\) 円 | \(1600\) 円 |
| B社 | \(\small 3~{\rm GB}\) 以下 | \(\small 7~{\rm GB}\) 以下 | \(\small 10~{\rm GB}\) 以下 |
| 料金 | \(500\) 円 | \(1000\) 円 | \(1500\) 円 |
\({\small (2)}~\)B社の通信量 \(x~{\rm GB}\) と料金 \(y\) 円の関係を表すグラフをかけ。
B社の表より、
\(0<x≦3\) のとき、\(y=500\)
\(3<x≦7\) のとき、\(y=1000\)
\(7<x≦10\) のとき、\(y=1500\)
であるので、グラフは、
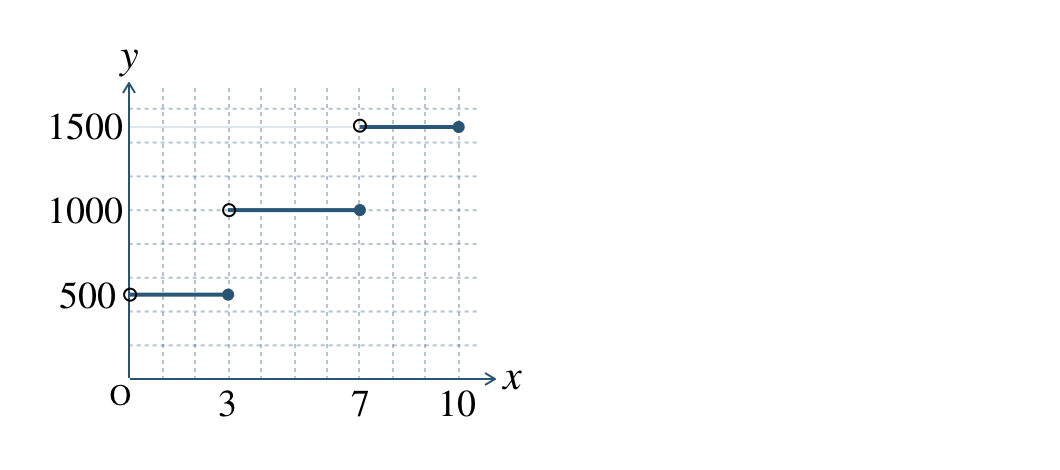
問題解説(3)
問題
次の表はA社とB社の通信量とその料金の表である。
| A社 | \(\small 5~{\rm GB}\) 以下 | \(\small 10~{\rm GB}\) 以下 |
| 料金 | \(800\) 円 | \(1600\) 円 |
| B社 | \(\small 3~{\rm GB}\) 以下 | \(\small 7~{\rm GB}\) 以下 | \(\small 10~{\rm GB}\) 以下 |
| 料金 | \(500\) 円 | \(1000\) 円 | \(1500\) 円 |
\({\small (3)}~\)次の通信量を使うとき、A社とB社のどちらか安いか答えよ。
① \(2~{\rm GB}\) ② \(4~{\rm GB}\)
③ \(6~{\rm GB}\) ④ \(8~{\rm GB}\)
A社とB社のグラフは、
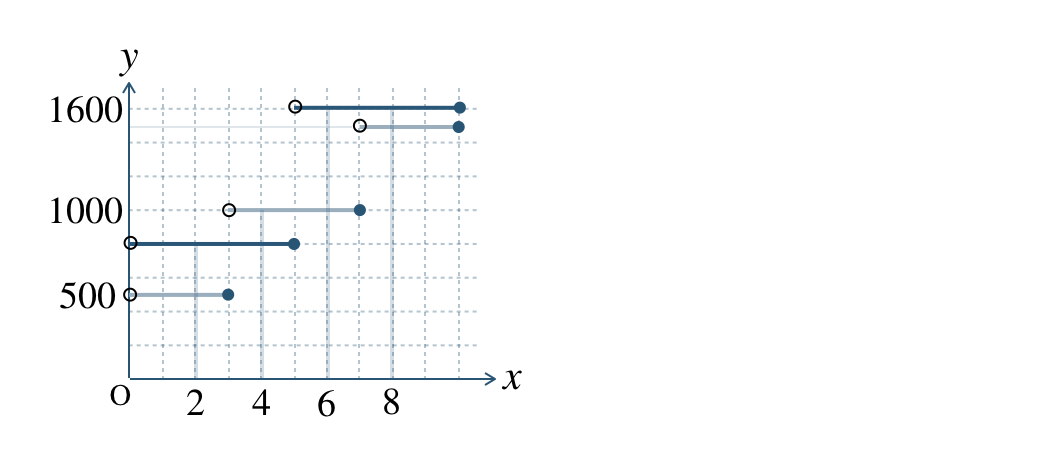
① \(2~{\rm GB}\)
\(x=2\) のときのグラフより、B社の方が安い
② \(4~{\rm GB}\)
\(x=4\) のときのグラフより、A社の方が安い
③ \(6~{\rm GB}\)
\(x=6\) のときのグラフより、B社の方が安い
④ \(8~{\rm GB}\)
\(x=8\) のときのグラフより、B社の方が安い

【問題一覧】中3|関数y=ax²
このページは「中学数学3 関数y=ax²」の問題一覧ページとなります。解説の見たい単元名がわからない...


