問題:円周角の定理と相似
次の証明をせよ。
\({\small (1)}~\)次の図で、弦 \({\rm AB}\) と弦 \({\rm CD}\) との交点を \({\rm P}\) とするとき、
\(\triangle {\rm PAC}\,\,\unicode{x223D}\,\,\triangle {\rm PDB}\)
であることを証明せよ。

\({\small (2)}~\)次の図で、弦 \({\rm AB}\) と弦 \({\rm CD}\) を延長した直線の交点を \({\rm P}\) とするとき、
\(\triangle {\rm PAD}\,\,\unicode{x223D}\,\,\triangle {\rm PCB}\)
であることを証明せよ。
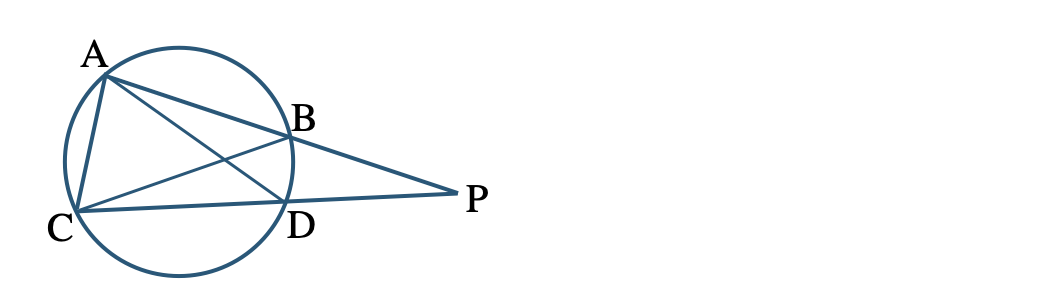
\({\small (3)}~\)次の図で、弦 \({\rm AB}\) と弦 \({\rm CD}\) との交点を \({\rm P}\) として、\(\overset{\frown}{{\rm CB}}=\overset{\frown}{{\rm BD}}\) であるとき、
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm ADP}\)
であることを証明せよ。

解法のPoint
■ 円周角の定理と相似
証明を書き始める前に、見通しをたてる。
・結論を導くために、示すべき相似な2つの三角形を見つける。
・仮定や仮定から導かれる根拠となることがらを考える。
・円周角の定理より、等しい角を根拠とする。
・根拠より、相似条件を考える。
\({\small (1)}~\)3組の辺の比がそれぞれ等しい
\({\small (2)}~\)2組の辺の比とその間の角がそれぞれ等しい
\({\small (3)}~\)2組の角がそれぞれ等しい
■ 証明のすすめ方
① 着目している三角形がどれとどれかを書く。
② 仮定から根拠となることがらを書く。
③ 仮定から導かられる根拠を書く。
④ 根拠から三角形の相似条件を書く。
⑤ 三角形が相似であることを記号 \(\,\unicode{x223D}\,\) で表す。
⑥ 相似な図形の性質より、結論を導く。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:円周角の定理と相似
問題解説(1)
次の証明をせよ。
\({\small (1)}~\)次の図で、弦 \({\rm AB}\) と弦 \({\rm CD}\) との交点を \({\rm P}\) とするとき、
\(\triangle {\rm PAC}\,\,\unicode{x223D}\,\,\triangle {\rm PDB}\)
であることを証明せよ。

・\(\triangle {\rm PAC}\) と \(\triangle {\rm PDB}\) に着目する
・円周角の定理より、\(\angle{\rm CAP}=\angle{\rm BDP}\)
・対頂角より、\(\angle{\rm APC}=\angle{\rm DPB}\)
・相似条件は、2組の角がそれぞれ等しい

[証明] \(\triangle {\rm PAC}\) と \(\triangle {\rm PDB}\) について、
\(\overset{\frown}{{\rm CB}}\) に対する円周角の定理より、
\(\angle{\rm CAP}=\angle{\rm BDP}~~~\cdots{\large ①}\)
対頂角が等しいので、
\(\angle{\rm APC}=\angle{\rm DPB}~~~\cdots{\large ②}\)
①、②より、2組の角がそれぞれ等しいので、
\(\triangle {\rm PAC}\,\,\unicode{x223D}\,\,\triangle {\rm PDB}\)
[終]
問題解説(2)
次の証明をせよ。
\({\small (2)}~\)次の図で、弦 \({\rm AB}\) と弦 \({\rm CD}\) を延長した直線の交点を \({\rm P}\) とするとき、
\(\triangle {\rm PAD}\,\,\unicode{x223D}\,\,\triangle {\rm PCB}\)
であることを証明せよ。

・\(\triangle {\rm PAD}\) と \(\triangle {\rm PCB}\) に着目する
・円周角の定理より、\(\angle{\rm PAD}=\angle{\rm PCB}\)
・共通の角より、\(\angle{\rm APD}=\angle{\rm CPB}\)
・相似条件は、2組の角がそれぞれ等しい
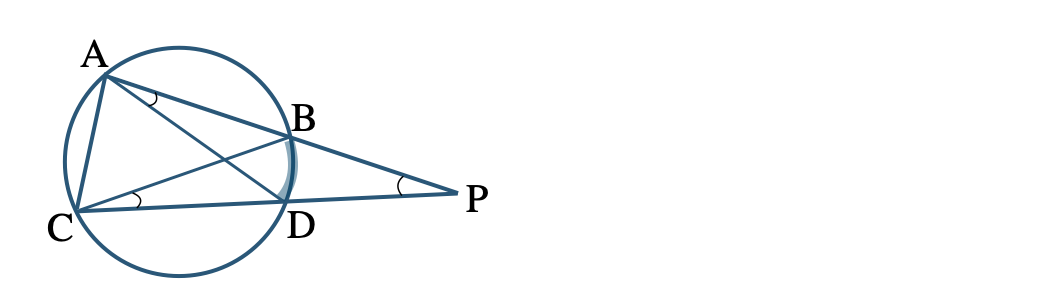
[証明] \(\triangle {\rm PAD}\) と \(\triangle {\rm PCB}\) について、
\(\overset{\frown}{{\rm BD}}\) に対する円周角の定理より、
\(\angle{\rm BAD}=\angle{\rm BCD}\)
よって、
\(\angle{\rm PAD}=\angle{\rm PCB}~~~\cdots{\large ①}\)
共通の角より、
\(\angle{\rm APD}=\angle{\rm CPB}~~~\cdots{\large ②}\)
①、②より、2組の角がそれぞれ等しいので、
\(\triangle {\rm PAD}\,\,\unicode{x223D}\,\,\triangle {\rm PCB}\)
[終]
問題解説(3)
次の証明をせよ。
\({\small (3)}~\)次の図で、弦 \({\rm AB}\) と弦 \({\rm CD}\) との交点を \({\rm P}\) として、\(\overset{\frown}{{\rm CB}}=\overset{\frown}{{\rm BD}}\) であるとき、
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm ADP}\)
であることを証明せよ。

・\(\triangle {\rm ABC}\) と \(\triangle {\rm ADP}\) に着目する
・仮定 \(\overset{\frown}{{\rm CB}}=\overset{\frown}{{\rm BD}}\) より、\(\angle{\rm CAB}=\angle{\rm PAD}\)
・円周角の定理より、\(\angle{\rm ABC}=\angle{\rm ADP}\)
・相似条件は、2組の角がそれぞれ等しい

[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm ADP}\) について、
仮定 \(\overset{\frown}{{\rm CB}}=\overset{\frown}{{\rm BD}}\) より、等しい弧に対する円周角が等しいので、
\(\angle{\rm CAB}=\angle{\rm BAD}\)
よって、
\(\angle{\rm CAB}=\angle{\rm PAD}~~~\cdots{\large ①}\)
また、\(\overset{\frown}{{\rm AC}}\) に対する円周角の定理より、
\(\angle{\rm ABC}=\angle{\rm ADC}\)
よって、
\(\angle{\rm ABC}=\angle{\rm ADP}~~~\cdots{\large ②}\)
①、②より、2組の角がそれぞれ等しいので、
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm ADP}\)
[終]



