問題:特別な直角三角形
問題
\({\small (1)}~\)次の図で、\(x~,~y\) の値を求めよ。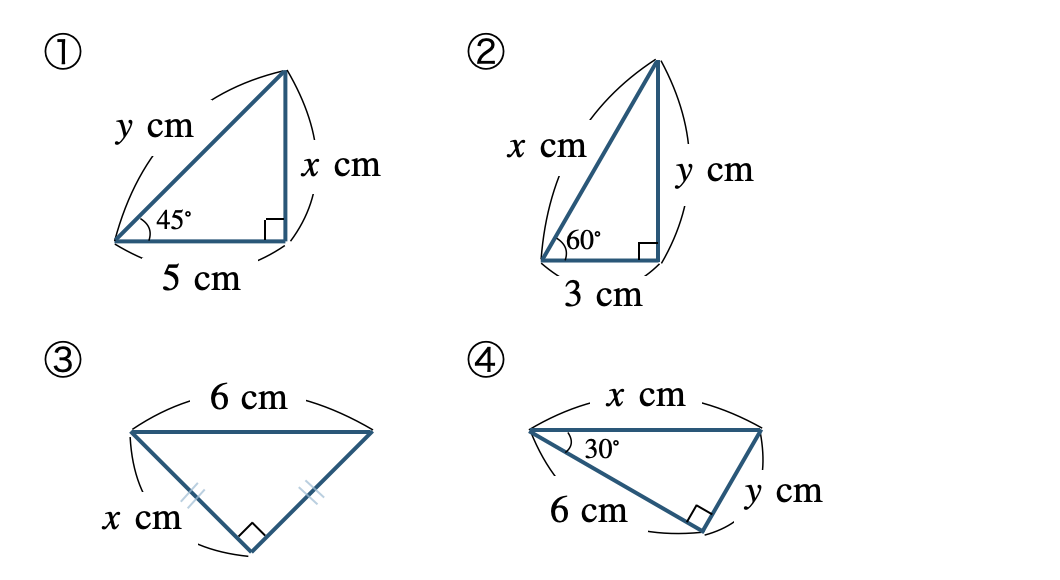

次の問いに答えよ。
\({\small (1)}~\)次の図で、\(x~,~y\) の値を求めよ。

\({\small (2)}~\)1組の三角定規を次のように合わせる。\({\rm AC}=6~{\rm cm}\) のとき、残りの辺の長さを求めよ。

解法のPoint
Point:特別な直角三角形
3辺の比は \(1:1:\sqrt{2}\) となる
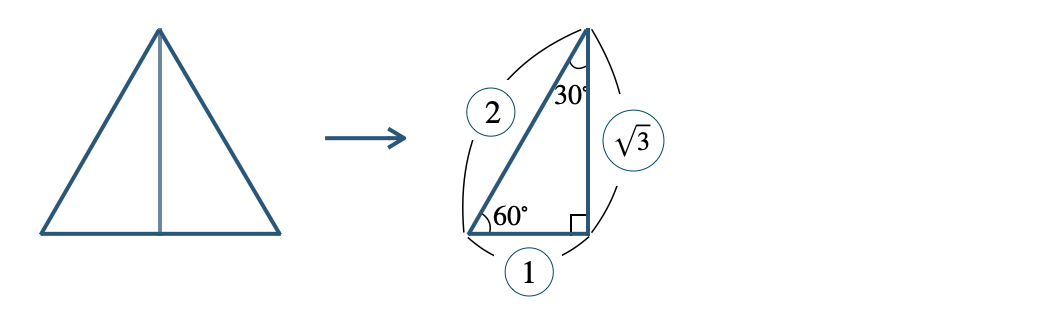
正三角形を高さで分けた直角三角形は、
角度が \(30^\circ~,~60^\circ~,~90^\circ\) となり、
3辺の比は \(1:2:\sqrt{3}\) となる
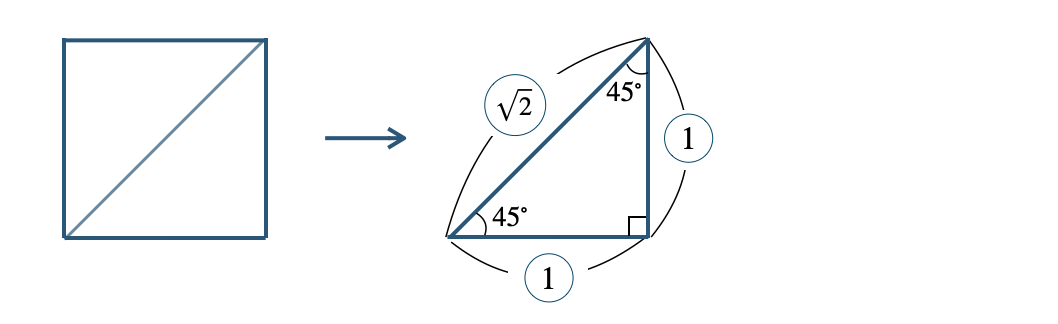
正方形を対角線で分けた直角三角形は、
角度が \(45^\circ~,~45^\circ~,~90^\circ\) となり、
3辺の比は \(1:1:\sqrt{2}\) となる

正三角形を高さで分けた直角三角形は、
角度が \(30^\circ~,~60^\circ~,~90^\circ\) となり、
3辺の比は \(1:2:\sqrt{3}\) となる

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:特別な直角三角形
問題解説(1)
問題
\({\small (1)}~\)次の図で、\(x~,~y\) の値を求めよ。
次の問いに答えよ。
\({\small (1)}~\)次の図で、\(x~,~y\) の値を求めよ。

① \(45^\circ~,~45^\circ~,~90^\circ\) の直角三角形となるので、3辺の比は \(1:1:\sqrt{2}\) となる
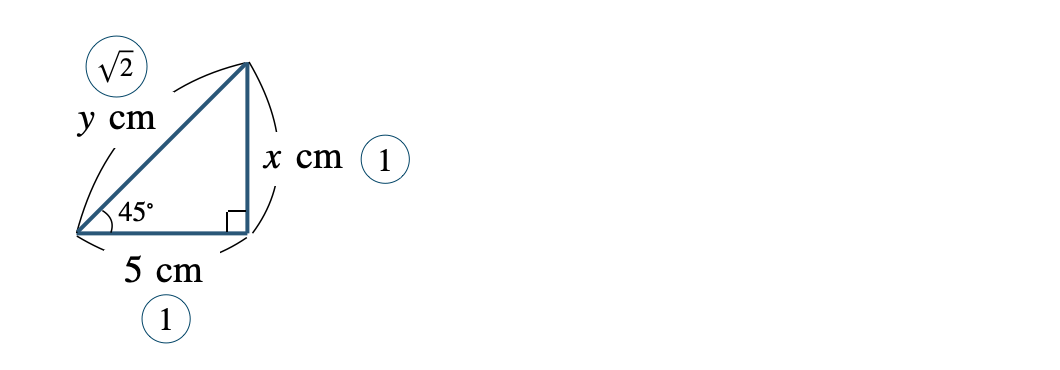
よって、
\(\begin{eqnarray}~~~5:x&=&1:1\\[2pt]~~~x{\, \small \times \,} 1&=&5{\, \small \times \,} 1\\[2pt]~~~x&=&5\end{eqnarray}\)
また、
\(\begin{eqnarray}~~~5:y&=&1:\sqrt{2}\\[2pt]~~~y{\, \small \times \,} 1&=&5{\, \small \times \,} \sqrt{2}\\[2pt]~~~y&=&5\sqrt{2}\end{eqnarray}\)
したがって、答えは
\(x=5~{\rm cm}~,~y=5\sqrt{2}~{\rm cm}\)
となる
② \(30^\circ~,~60^\circ~,~90^\circ\) の直角三角形となるので、3辺の比は \(1:2:\sqrt{3}\) となる

よって、
\(\begin{eqnarray}~~~3:x&=&1:2\\[2pt]~~~x{\, \small \times \,} 1&=&3{\, \small \times \,}2\\[2pt]~~~x&=&6\end{eqnarray}\)
また、
\(\begin{eqnarray}~~~3:y&=&1:\sqrt{3}\\[2pt]~~~y{\, \small \times \,} 1&=&3{\, \small \times \,}\sqrt{3}\\[2pt]~~~y&=&3\sqrt{3}\end{eqnarray}\)
したがって、答えは
\(x=6~{\rm cm}~,~y=3\sqrt{3}~{\rm cm}\)
となる
③ 二等辺三角形であり、底角が \(45^\circ\) となる
よって、\(45^\circ~,~45^\circ~,~90^\circ\) の直角三角形となるので、3辺の比は \(1:1:\sqrt{2}\) となる

よって、
\(\begin{eqnarray}~~~x:6&=&1:\sqrt{2}\\[2pt]~~~x{\, \small \times \,} \sqrt{2}&=&6{\, \small \times \,}1\\[2pt]~~~\sqrt{2}x&=&6\\[3pt]~~~\frac{\,\sqrt{2}x\,}{\,\sqrt{2}\,}&=&\frac{\,6\,}{\,\sqrt{2}\,}\\[3pt]~~~x&=&\frac{\,6{\, \small \times \,}\sqrt{2}\,}{\,\sqrt{2}{\, \small \times \,}\sqrt{2}\,}\\[3pt]~~~x&=&\frac{\,6\sqrt{2}\,}{\,2\,}\\[3pt]~~~x&=&3\sqrt{2}\end{eqnarray}\)
したがって、答えは
\(x=3\sqrt{2}~{\rm cm}\)
となる
④ \(30^\circ~,~60^\circ~,~90^\circ\) の直角三角形となるので、3辺の比は \(1:2:\sqrt{3}\) となる

よって、
\(\begin{eqnarray}~~~x:6&=&2:\sqrt{3}\\[2pt]~~~x{\, \small \times \,} \sqrt{3}&=&6{\, \small \times \,}2\\[2pt]~~~\sqrt{3}x&=&12\\[3pt]~~~\frac{\,\sqrt{3}x\,}{\,\sqrt{3}\,}&=&\frac{\,12\,}{\,\sqrt{3}\,}\\[3pt]~~~x&=&\frac{\,12{\, \small \times \,}\sqrt{3}\,}{\,\sqrt{3}{\, \small \times \,}\sqrt{3}\,}\\[3pt]~~~x&=&\frac{\,12\sqrt{3}\,}{\,3\,}\\[3pt]~~~x&=&4\sqrt{3}\end{eqnarray}\)
また、\(x=4\sqrt{3}\) より、
\(\begin{eqnarray}~~~4\sqrt{3}:y&=&2:1\\[2pt]~~~y{\, \small \times \,} 2&=&4\sqrt{3} {\, \small \times \,} 1\\[2pt]~~~2y&=&4\sqrt{3}\\[3pt]~~~\frac{\,2y\,}{\,2\,}&=&\frac{\,4\sqrt{3}\,}{\,2\,}\\[3pt]~~~y&=&2\sqrt{3}\end{eqnarray}\)
したがって、答えは
\(x=4\sqrt{3}~{\rm cm}~,~y=2\sqrt{3}~{\rm cm}\)
となる
問題解説(2)
問題
\({\small (2)}~\)1組の三角定規を次のように合わせる。\({\rm AC}=6~{\rm cm}\) のとき、残りの辺の長さを求めよ。
次の問いに答えよ。
\({\small (2)}~\)1組の三角定規を次のように合わせる。\({\rm AC}=6~{\rm cm}\) のとき、残りの辺の長さを求めよ。

\(\triangle {\rm ABC}\) は、\(45^\circ~,~45^\circ~,~90^\circ\) の直角三角形となるので、3辺の比は \(1:1:\sqrt{2}\) となる

よって、
\(\begin{eqnarray}~~~{\rm AB}:6&=&1:\sqrt{2}\\[2pt]~~~{\rm AB}{\, \small \times \,}\sqrt{2}&=&6{\, \small \times \,}1\\[2pt]~~~\sqrt{2}{\rm AB}&=&6\\[3pt]~~~\frac{\,\sqrt{2}{\rm AB}\,}{\,\sqrt{2}\,}&=&\frac{\,6\,}{\,\sqrt{2}\,}\\[3pt]~~~{\rm AB}&=&\frac{\,6{\, \small \times \,}\sqrt{2}\,}{\,\sqrt{2}{\, \small \times \,}\sqrt{2}\,}\\[3pt]~~~{\rm AB}&=&\frac{\,6\sqrt{2}\,}{\,2\,}\\[3pt]~~~{\rm AB}&=&3\sqrt{2}\end{eqnarray}\)
また、\({\rm AB:BC}=1:1\) より、
\(~~~{\rm BC}=3\sqrt{2}\)
次に、\(\triangle {\rm ACD}\) は、\(30^\circ~,~60^\circ~,~90^\circ\) の直角三角形となるので、3辺の比は \(1:2:\sqrt{3}\) となる

よって、
\(\begin{eqnarray}~~~{\rm CD}:6&=&1:\sqrt{3}\\[2pt]~~~{\rm CD}{\, \small \times \,}\sqrt{3}&=&6{\, \small \times \,}1\\[2pt]~~~\sqrt{3}{\rm CD}&=&6\\[3pt]~~~\frac{\,\sqrt{3}{\rm CD}\,}{\,\sqrt{3}\,}&=&\frac{\,6\,}{\,\sqrt{3}\,}\\[3pt]~~~{\rm CD}&=&\frac{\,6{\, \small \times \,}\sqrt{3}\,}{\,\sqrt{3}{\, \small \times \,}\sqrt{3}\,}\\[3pt]~~~{\rm CD}&=&\frac{\,6\sqrt{3}\,}{\,3\,}\\[3pt]~~~{\rm CD}&=&2\sqrt{3}\end{eqnarray}\)
また、\({\rm CD:AD}=1:2\) より、
\(\begin{eqnarray}~~~2\sqrt{3}:{\rm AD}&=&1:2\\[2pt]~~~{\rm AD}{\, \small \times \,}1&=&2\sqrt{3}{\, \small \times \,}2\\[2pt]~~~{\rm AD}&=&4\sqrt{3}\end{eqnarray}\)
したがって、答えは
\({\rm AB}=3\sqrt{2}~{\rm cm}~,~{\rm BC}=3\sqrt{2}~{\rm cm}\)
\({\rm CD}=2\sqrt{3}~{\rm cm}~,~{\rm AD}=4\sqrt{3}~{\rm cm}\)
となる

【問題一覧】中3|三平方の定理
このページは「中学数学3 三平方の定理」の問題一覧ページとなります。解説の見たい単元名がわからないと...


