問題:図形と三平方の定理
次の問いに答えよ。
\({\small (1)}~\)次の長方形の対角線の長さを求めよ。

\({\small (2)}~\)1辺の長さが \(6~{\rm cm}\) の正三角形 \(\triangle {\rm ABC}\) の面積を求めよ。
\({\small (3)}~\)次の二等辺三角形 \(\triangle {\rm ABC}\) の面積を求めよ。

解法のPoint
長方形の対角線の求め方は、
① 対角線 \(x~{\rm cm}\) で分けた直角三角形を考える。

② この直角三角形の三平方の定理より、対角線 \(x~{\rm cm}\) を求める。
\(\begin{eqnarray}~~~a^2+b^2&=&x^2\\[2pt]~~~x&=&\sqrt{a^2+b^2}\end{eqnarray}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
正三角形の面積の求め方は、
① 正三角形を高さ \(h~{\rm cm}\) で分けた直角三角形を考える。
このとき、正三角形の高さは垂線となり、底辺を二等分する。

② \(1:2:\sqrt{3}\) の直角三角形より、高さ \(h~{\rm cm}\) を求める。
\(\begin{eqnarray}~~~2:\sqrt{3}&=&a:h\\[3pt]~~~h&=&\frac{\,\sqrt{3}\,}{\,2\,}a\end{eqnarray}\)
③ 底辺 \(a~{\rm cm}\) と高さ \(h~{\rm cm}\)より、正三角形の面積を求める。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
二等辺三角形の面積の求め方は、
① 二等辺三角形を高さ \(h~{\rm cm}\) で分けた直角三角形を考える。
このとき、二等辺三角形の高さは垂線となり、底辺を二等分する。
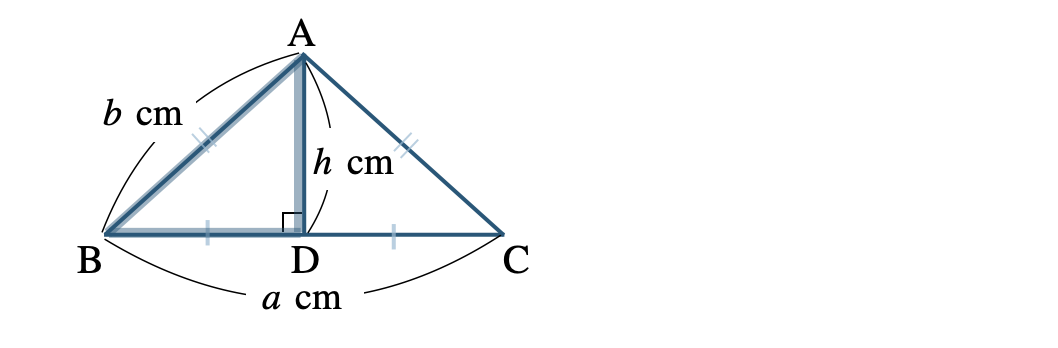
② この直角三角形の三平方の定理より、高さ \(h~{\rm cm}\) を求める。
\(\begin{eqnarray}~~~\left(\frac{\,a\,}{\,2\,}\right)^2+h^2&=&b^2\\[3pt]~~~h&=&\sqrt{b^2-\frac{\,a^2\,}{\,4\,}}\end{eqnarray}\)
③ 底辺 \(a~{\rm cm}\) と高さ \(h~{\rm cm}\)より、二等辺三角形の面積を求める。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:図形と三平方の定理
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の長方形の対角線の長さを求めよ。

対角線の長さを \(x~{\rm cm}\) とすると、

これより、斜辺 \(x~{\rm cm}\) の直角三角形となり、三平方の定理より、
\(\begin{eqnarray}~~~\left(2\sqrt{5}\right)^2+4^2&=&x^2\\[2pt]~~~20+16&=&x^2\\[2pt]~~~36&=&x^2\\[2pt]~~~x^2&=&36\end{eqnarray}\)
\(x>0\) より、
\(~~~x=\sqrt{36}=\sqrt{6^2}=6\)
したがって、答えは \(6~{\rm cm}\) となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)1辺の長さが \(6~{\rm cm}\) の正三角形 \(\triangle {\rm ABC}\) の面積を求めよ。
正三角形 \(\triangle {\rm ABC}\) の高さを \(h~{\rm cm}\) とすると、垂線 \({\rm AD}\) は底辺 \({\rm BC}\) を二等分する

\(\triangle {\rm ABD}\) は \(1:2:\sqrt{3}\) の直角三角形となるので、
\(\begin{eqnarray}~~~1:\sqrt{3}&=&3:h\\[2pt]~~~1\times h&=&\sqrt{3} \times3\\[2pt]~~~h&=&3\sqrt{3}\end{eqnarray}\)
よって、正三角形の面積は底辺 \(6~{\rm cm}\)、高さ \(3\sqrt{3}~{\rm cm}\) より、
\(~~~\frac{\,1\,}{\,2\,}\times6\times3\sqrt{3}=9\sqrt{3}\)
したがって、答えは \(9\sqrt{3}~{\rm cm}^2\) となる
問題解説(3)
次の問いに答えよ。
\({\small (3)}~\)次の二等辺三角形 \(\triangle {\rm ABC}\) の面積を求めよ。

二等辺三角形 \(\triangle {\rm ABC}\) の高さを \(h~{\rm cm}\) とすると、垂線 \({\rm AD}\) は底辺 \({\rm BC}\) を二等分する
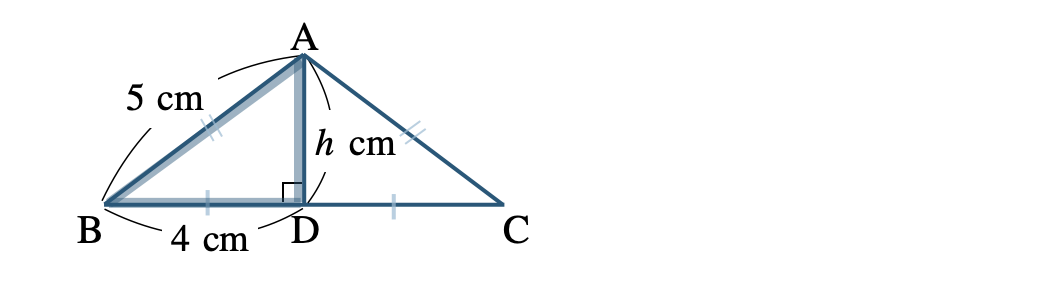
\(\triangle {\rm ABD}\) は直角三角形であり、三平方の定理より、
\(\begin{eqnarray}~~~4^2+h^2&=&5^2\\[2pt]~~~16+h^2&=&25\\[2pt]~~~h^2&=&25-16\\[2pt]~~~h^2&=&9\end{eqnarray}\)
\(h>0\) より、
\(~~~h=\sqrt{9}=\sqrt{3^2}=3\)
よって、二等辺三角形の面積は底辺 \(8~{\rm cm}\)、高さ \(3~{\rm cm}\) より、
\(~~~\frac{\,1\,}{\,2\,}\times8\times3=12\)
したがって、答えは \(12~{\rm cm}^2\) となる



