円と三平方の定理

円と三平方の定理の解法
問題解説：円と三平方の定理
1. 問題解説(1)
2. 問題解説(2)

円と三平方の定理の解法

Point：円の弦の長さと三平方の定理

円の弦の長さの求め方は、

① 円の中心 \({\rm O}\) から弦 \({\rm AB}\) に垂線 \({\rm OH}\) を引くと、\(\triangle {\rm OAB}\) が二等辺三角形であるので、弦 \({\rm AB}\) を二等分する。

② \(\triangle {\rm OAH}\) は直角三角形となり三平方の定理より、\(x\) の長さを求める。

\(\begin{eqnarray}~~~x^2+h^2&=&r^2\\[2pt]~~~x&=&\sqrt{r^2-h^2}\end{eqnarray}\)

③ \({\rm AB}=2x\) より、弦の長さを求める。

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

Point：円の接線の長さと三平方の定理

円の接線の長さの求め方は、

① 円の接線と半径は垂直に交わるので、\(\triangle {\rm APO}\) は \(\angle{\rm APO}=90^\circ\) の直角三角形となる。

② 三平方の定理より、接線の長さ \({\rm AP}\) を求める。

\(\begin{eqnarray}~~~x^2+r^2&=&a^2\\[2pt]~~~x&=&\sqrt{a^2-r^2}\end{eqnarray}\)

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題解説：円と三平方の定理

問題解説(1)

問題

次の問いに答えよ。

\({\small (1)}~\)半径 \(6~{\rm cm}\) の円 \({\rm O}\) において、中心 \({\rm O}\) からの距離が \(3~{\rm cm}\) である弦 \({\rm AB}\) の長さを求めよ。

円の中心 \({\rm O}\) から弦 \({\rm AB}\) に垂線 \({\rm OH}\) を引くと、
\(\triangle {\rm OAB}\) が二等辺三角形であるので、弦 \({\rm AB}\) を二等分する

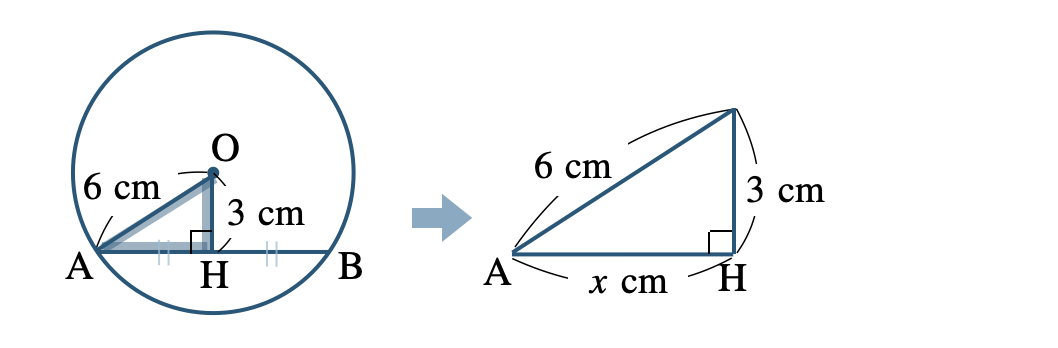
\({\rm AH}=x~{\rm cm}\) として、\(\triangle {\rm OAH}\) は直角三角形であるので三平方の定理より、

\(\begin{eqnarray}~~~x^2+3^2&=&6^2\\[2pt]~~~x^2+9&=&36\\[2pt]~~~x^2&=&36-9\\[2pt]~~~x^2&=&27\end{eqnarray}\)

\(x>0\) より、

\(~~~x=\sqrt{27}=\sqrt{3^2\times3}=3\sqrt{3}\)

ここで、\({\rm AB}=2x\) より、

\(~~~{\rm AB}=2\times3\sqrt{3}=6\sqrt{3}~{\rm cm}\)

したがって、答えは \(6\sqrt{3}~{\rm cm}\) となる

問題解説(2)

問題

次の問いに答えよ。

\({\small (2)}~\)次の図で、直線 \({\rm AP}\) は円 \({\rm O}\) の接線で、点 \({\rm P}\) は接点である。円 \({\rm O}\) の半径が \(6~{\rm cm}\)、\({\rm AO}=12~{\rm cm}\) のとき、接線 \({\rm AP}\) の長さを求めよ。