√nの作図

Point：√nの作図

１辺が \(1~{\rm cm}\) の正方形において、

① 対角線 \({\rm AC}\) は三平方の定理より、\({\rm AC}=\sqrt{2}\) となる。

---

② コンパスで、点 \({\rm A}\) が中心で半径 \({\rm AC}=\sqrt{2}\) の円をかき、直線 \({\rm AB}\) との交点を \({\rm E}\) とすると、\({\rm AE}=\sqrt{2}\) となる。

---

また、長方形 \({\rm AEFB}\) において、

③ 対角線 \({\rm AF}\) は三平方の定理より、\({\rm AF}=\sqrt{3}\) となる。

---

④ コンパスで、点 \({\rm A}\) が中心で半径 \({\rm AF}=\sqrt{2}\) の円をかき、直線 \({\rm AB}\) との交点を \({\rm G}\) とすると、\({\rm AG}=\sqrt{3}\) となる。

---

これをくり返すことで、\(\sqrt{5}~,~\sqrt{6}~,~\cdots\) とルートの数を作図できる。

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次の図において、下の問いに答えよ。

---

\({\small (1)}~\)直線 \({\rm AB}\) 上に \(\sqrt{2}\) を作図せよ。

① 正方形 \({\rm ABCD}\) の対角線 \({\rm AC}\) は三平方の定理より、

---

\(\begin{eqnarray}~~~1^2+1^2&=&{\rm AC}^2\\[2pt]~~~{\rm AC}^2&=&2\end{eqnarray}\)

---

\({\rm AC}>0\) より、\({\rm AC}=\sqrt{2}\) となる

---

② コンパスで、点 \({\rm A}\) が中心で半径 \({\rm AC}=\sqrt{2}\) の円をかき、直線 \({\rm AB}\) との交点を \({\rm E}\) とすると、

これより、
　\({\rm AE}=\sqrt{2}\)
となる

問題

次の図において、下の問いに答えよ。

---

\({\small (2)}~\)\(\sqrt{2}\) の長さを使って、直線 \({\rm AB}\) 上に \(\sqrt{3}\) を作図せよ。

① (1)より、横の長さが \(\sqrt{2}\) の長方形 \({\rm AEFD}\) をかくと、

---

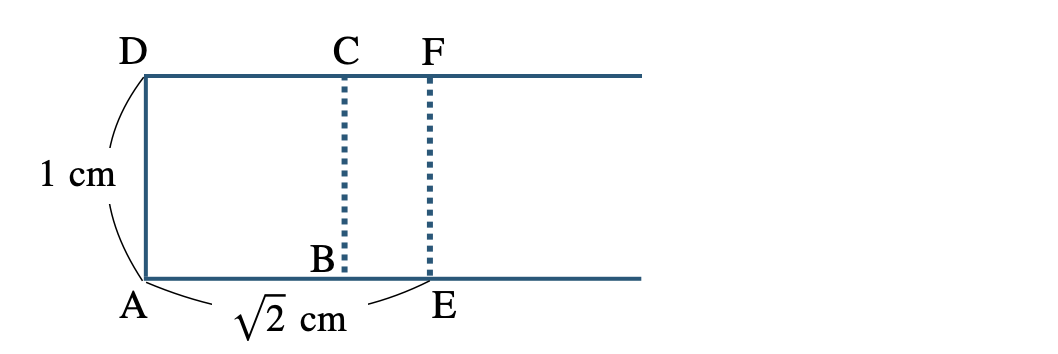
② 長方形 \({\rm AEFD}\) の対角線 \({\rm AF}\) は三平方の定理より、

---

\(\begin{eqnarray}~~~1^2+\left(\sqrt{2}\right)^2&=&{\rm AF}^2\\[2pt]~~~{\rm AF}^2&=&3\end{eqnarray}\)

---

\({\rm AF}>0\) より、\({\rm AF}=\sqrt{3}\) となる

---

③ コンパスで、点 \({\rm A}\) が中心で半径 \({\rm AF}=\sqrt{3}\) の円をかき、直線 \({\rm AB}\) との交点を \({\rm G}\) とすると、

これより、
　\({\rm AG}=\sqrt{3}\)
となる

問題

次の図において、下の問いに答えよ。

---

\({\small (3)}~\)直線 \({\rm AB}\) 上に \(\sqrt{5}\) を作図せよ。

① 直線 \({\rm AB}\) 上に \({\rm AH}=2\) となる点 \({\rm H}\) をとり、長方形 \({\rm AHID}\) をかくと、

---

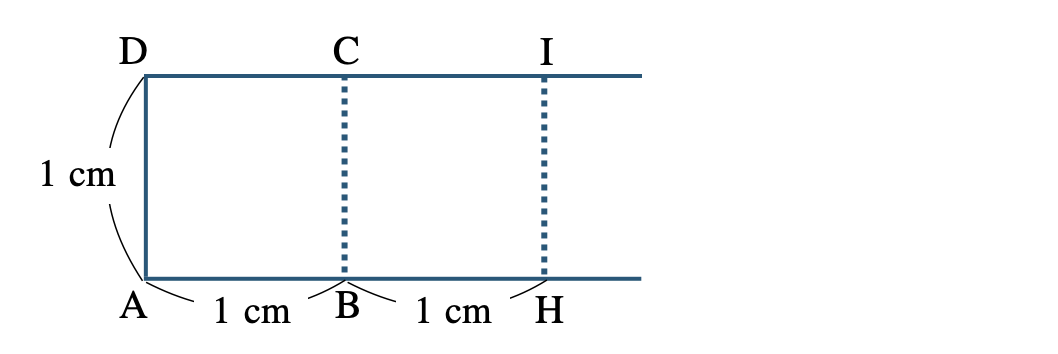
② 長方形 \({\rm AHID}\) の対角線 \({\rm AI}\) は三平方の定理より、

---

\(\begin{eqnarray}~~~1^2+2^2&=&{\rm AI}^2\\[2pt]~~~{\rm AI}^2&=&5\end{eqnarray}\)

---

\({\rm AI}>0\) より、\({\rm AI}=\sqrt{5}\) となる

---

③ コンパスで、点 \({\rm A}\) が中心で半径 \({\rm AI}=\sqrt{5}\) の円をかき、直線 \({\rm AB}\) との交点を \({\rm J}\) とすると、

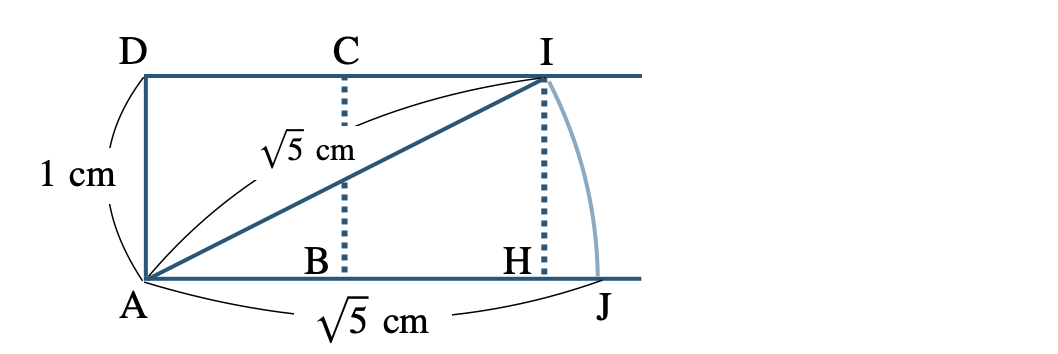
これより、
　\({\rm AJ}=\sqrt{5}\)
となる