座標上の２点間の距離の解法
２点 \({\rm A}(-2~,~1)~,~{\rm B}(2~,~3)\) 間の距離 \({\rm AB}\) の求め方は、
① ２点の位置を座標上にかく。
※ おおよその位置でよい。
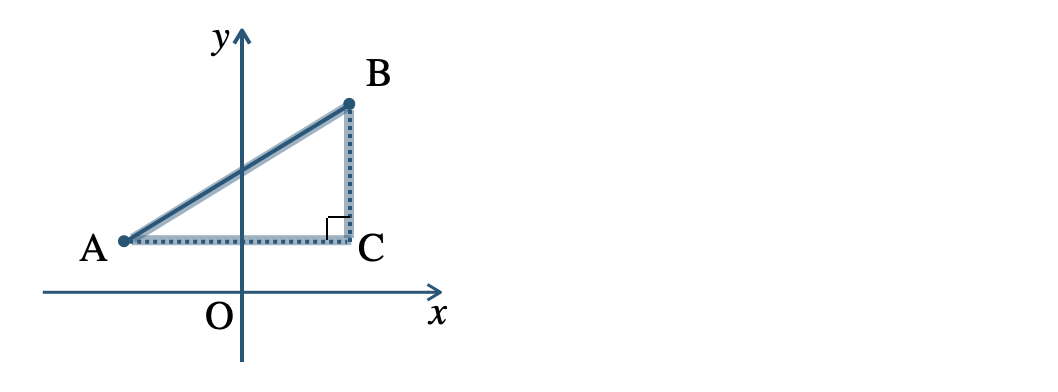
② 線分 \({\rm AB}\) を斜辺とする \(\angle{\rm C}=90^\circ\) の直角三角形 \(\triangle {\rm ABC}\) をかく。
③ \({\rm AC}=x\) 座標の差、\({\rm BC}=y\) 座標の差より、\({\rm AC~,~BC}\) の長さを求める。
\(~~~{\rm AC}=2-(-2)=4~,~{\rm BC}=3-1=2\)
④ 三平方の定理より、\({\rm AB}\) の長さを求める。
\(\begin{eqnarray}~~~4^2+2^2&=&{\rm AB}^2\\[2pt]~~~{\rm AB}&=&2\sqrt{5}\end{eqnarray}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説：座標上の２点間の距離
問題解説(1)
次の２点間の距離 \({\rm AB}\) を求めよ。
\({\small (1)}~{\rm A}(2~,~1)~,~{\rm B}(5~,~4)\)
２点 \({\rm A~,~B}\) の位置を座標上にかき、線分 \({\rm AB}\) を斜辺とする \(\angle{\rm C}=90^\circ\) の直角三角形 \(\triangle {\rm ABC}\) をかくと、
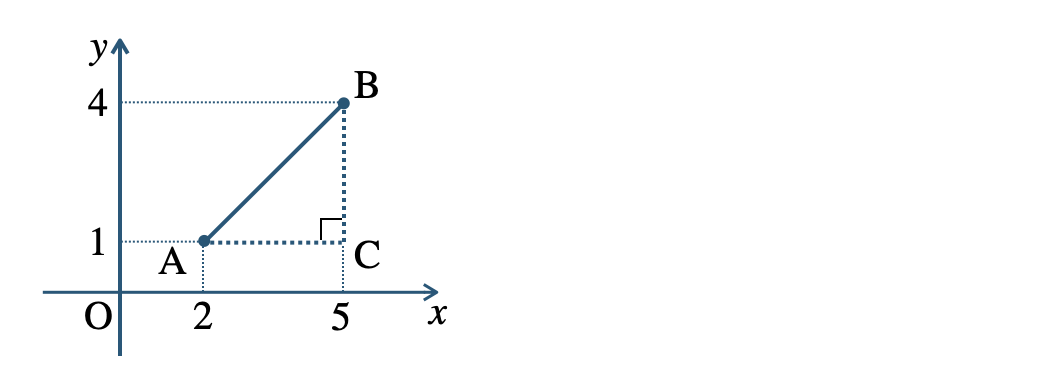
\(\begin{eqnarray}~~~{\rm AC}&=&5-2=3\\[2pt]~~~{\rm BC}&=&4-1=3\end{eqnarray}\)
三平方の定理より、
\(\begin{eqnarray}~~~3^2+3^2&=&{\rm AB}^2\\[2pt]~~~9+9&=&{\rm AB}^2\\[2pt]~~~{\rm AB}^2&=&18\end{eqnarray}\)
\({\rm AB}>0\) より、
\(~~~{\rm AB}=\sqrt{18}=\sqrt{3^2\times2}=3\sqrt{2}\)
したがって、答えは \({\rm AB}=3\sqrt{2}\) となる
問題解説(2)
次の２点間の距離 \({\rm AB}\) を求めよ。
\({\small (2)}~{\rm A}(-1~,~3)~,~{\rm B}(2~,~-1)\)
２点 \({\rm A~,~B}\) の位置を座標上にかき、線分 \({\rm AB}\) を斜辺とする \(\angle{\rm C}=90^\circ\) の直角三角形 \(\triangle {\rm ABC}\) をかくと、
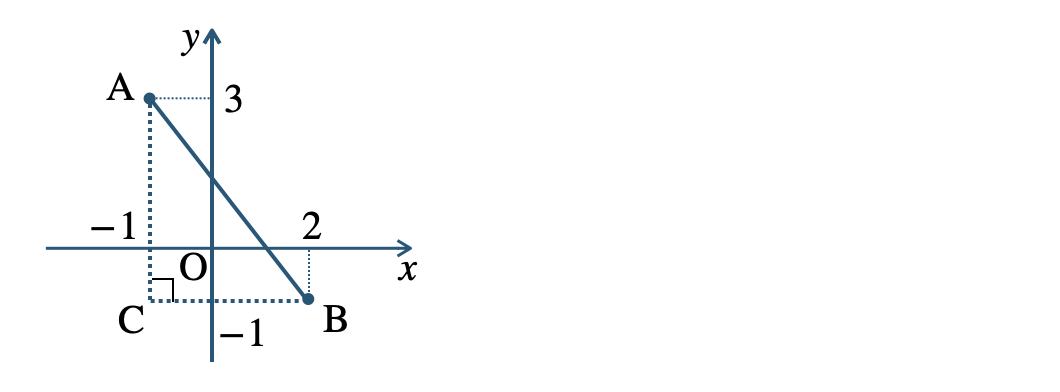
\(\begin{eqnarray}~~~{\rm AC}&=&2-(-1)=2+1=3\\[2pt]~~~{\rm BC}&=&3-(-1)=3+1=4\end{eqnarray}\)
三平方の定理より、
\(\begin{eqnarray}~~~3^2+4^2&=&{\rm AB}^2\\[2pt]~~~9+16&=&{\rm AB}^2\\[2pt]~~~{\rm AB}^2&=&25\end{eqnarray}\)
\({\rm AB}>0\) より、
\(~~~{\rm AB}=\sqrt{25}=\sqrt{5^2}=5\)
したがって、答えは \({\rm AB}=5\) となる
問題解説(3)
次の２点間の距離 \({\rm AB}\) を求めよ。
\({\small (3)}~{\rm A}(3~,~-5)~,~{\rm B}(-2~,~7)\)
２点 \({\rm A~,~B}\) の位置を座標上にかき、線分 \({\rm AB}\) を斜辺とする \(\angle{\rm C}=90^\circ\) の直角三角形 \(\triangle {\rm ABC}\) をかくと、
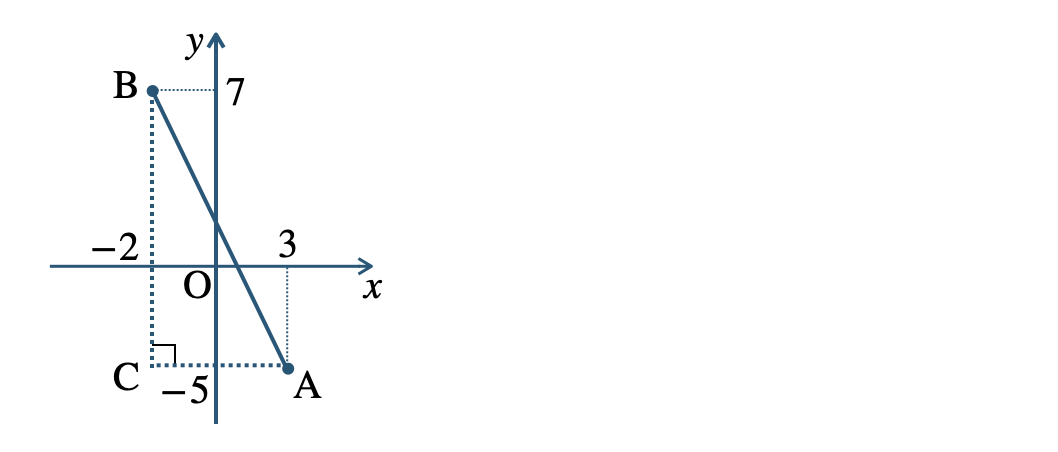
\(\begin{eqnarray}~~~{\rm AC}&=&3-(-2)=3+2=5\\[2pt]~~~{\rm BC}&=&7-(-5)=7+5=12\end{eqnarray}\)
三平方の定理より、
\(\begin{eqnarray}~~~5^2+12^2&=&{\rm AB}^2\\[2pt]~~~25+144&=&{\rm AB}^2\\[2pt]~~~{\rm AB}^2&=&169\end{eqnarray}\)
\({\rm AB}>0\) より、
\(~~~{\rm AB}=\sqrt{169}=\sqrt{13^2}=13\)
したがって、答えは \({\rm AB}=13\) となる
問題解説(4)
次の２点間の距離 \({\rm AB}\) を求めよ。
\({\small (4)}~{\rm A}(4~,~5)~,~{\rm B}(-4~,~1)\)
２点 \({\rm A~,~B}\) の位置を座標上にかき、線分 \({\rm AB}\) を斜辺とする \(\angle{\rm C}=90^\circ\) の直角三角形 \(\triangle {\rm ABC}\) をかくと、
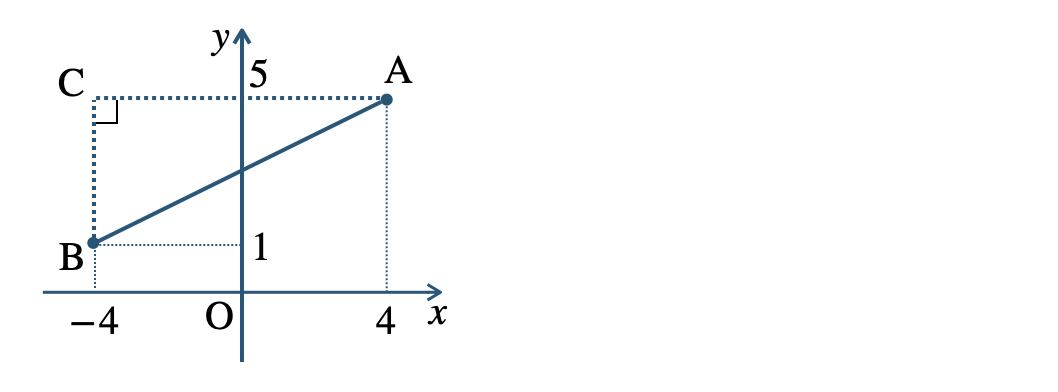
\(\begin{eqnarray}~~~{\rm AC}&=&4-(-4)=4+4=8\\[2pt]~~~{\rm BC}&=&5-1=4\end{eqnarray}\)
三平方の定理より、
\(\begin{eqnarray}~~~8^2+4^2&=&{\rm AB}^2\\[2pt]~~~64+16&=&{\rm AB}^2\\[2pt]~~~{\rm AB}^2&=&80\end{eqnarray}\)
\({\rm AB}>0\) より、
\(~~~{\rm AB}=\sqrt{80}=\sqrt{4^2\times5}=4\sqrt{5}\)
したがって、答えは \({\rm AB}=4\sqrt{5}\) となる
