問題:角錐や円錐と三平方の定理
問題
\({\small (1)}~\)次の正四角錐の高さと体積を求めよ。

次の問いに答えよ。
\({\small (1)}~\)次の正四角錐の高さと体積を求めよ。

\({\small (2)}~\)次の円錐の高さと体積を求めよ。

解法のPoint
Point:角錐と三平方の定理
① 正方形 \({\rm ABCD}\) の対角線の交点を \({\rm H}\) として、三平方の定理より \({\rm AC}\) を求めて \({\rm AH}\) を求める。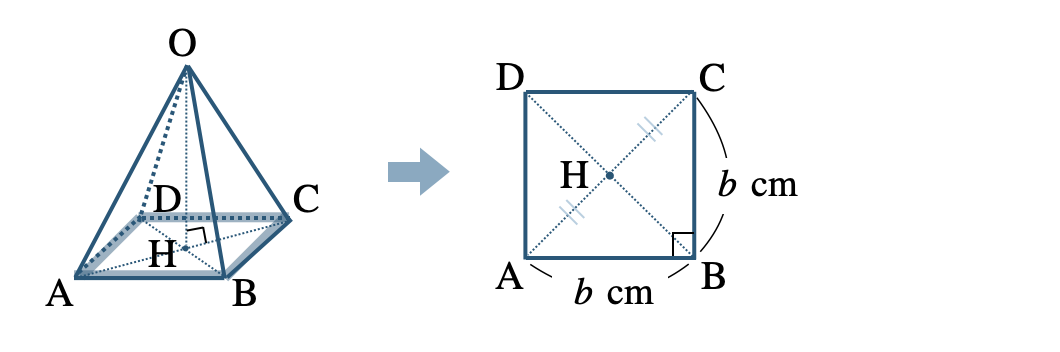
② \(\triangle {\rm OAH}\) は直角三角形であるので、三平方の定理より \({\rm OH}\) を求める。
\(\begin{eqnarray}~~~{\rm OH}^2+{\rm AH}^2&=&a^2\\[2pt]~~~{\rm OH}&=&\sqrt{a^2-{\rm AH}^2}\end{eqnarray}\)
③ 高さと底面積より、体積を求める。
\(\begin{split}{\rm V}={\frac{\,1\,}{\,3\,}}{\, \small \times \,}\end{split}\)(正方形 \({\rm ABCD}\) の面積)\(\begin{split}{\, \small \times \,} {\rm OH}\end{split}\)
正四角錐の母線の長さが \(a~{\rm cm}\)、底面の正方形の1辺の長さが \(b~{\rm cm}\) のとき、高さと体積は、
① 正方形 \({\rm ABCD}\) の対角線の交点を \({\rm H}\) として、三平方の定理より \({\rm AC}\) を求めて \({\rm AH}\) を求める。

\({\rm AC}=\sqrt{2}b\) より、\(\begin{split}{\rm AH}=\frac{\,\sqrt{2}\,}{\,2\,}b\end{split}\)
② \(\triangle {\rm OAH}\) は直角三角形であるので、三平方の定理より \({\rm OH}\) を求める。
\(\begin{eqnarray}~~~{\rm OH}^2+{\rm AH}^2&=&a^2\\[2pt]~~~{\rm OH}&=&\sqrt{a^2-{\rm AH}^2}\end{eqnarray}\)
③ 高さと底面積より、体積を求める。
\(\begin{split}{\rm V}={\frac{\,1\,}{\,3\,}}{\, \small \times \,}\end{split}\)(正方形 \({\rm ABCD}\) の面積)\(\begin{split}{\, \small \times \,} {\rm OH}\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:円錐と三平方の定理
① 断面の \(\triangle {\rm ABO}\) は直角三角形であるので、三平方の定理より高さ \({\rm AO}\) を求める。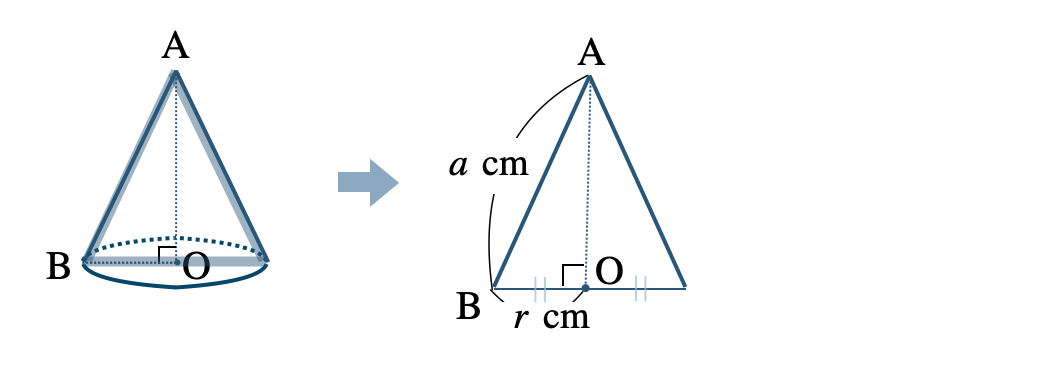
② 高さと底面積より、体積を求める。
\(\begin{split}{\rm V}={\frac{\,1\,}{\,3\,}}{\, \small \times \,}\end{split}\)(円の面積)\(\begin{split}{\, \small \times \,} {\rm AO}\end{split}\)
円錐の母線の長さが \(a~{\rm cm}\)、底面の円の半径が \(r~{\rm cm}\) のとき、高さと体積は、
① 断面の \(\triangle {\rm ABO}\) は直角三角形であるので、三平方の定理より高さ \({\rm AO}\) を求める。

\(\begin{eqnarray}~~~{\rm AO}^2+r^2&=&a^2\\[2pt]~~~{\rm AO}&=&\sqrt{a^2-r^2}\end{eqnarray}\)
② 高さと底面積より、体積を求める。
\(\begin{split}{\rm V}={\frac{\,1\,}{\,3\,}}{\, \small \times \,}\end{split}\)(円の面積)\(\begin{split}{\, \small \times \,} {\rm AO}\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:角錐や円錐と三平方の定理
問題解説(1)
問題
\({\small (1)}~\)次の正四角錐の高さと体積を求めよ。
次の問いに答えよ。
\({\small (1)}~\)次の正四角錐の高さと体積を求めよ。

底面の正方形 \({\rm ABCD}\) の対角線の交点が \({\rm H}\) とすると、
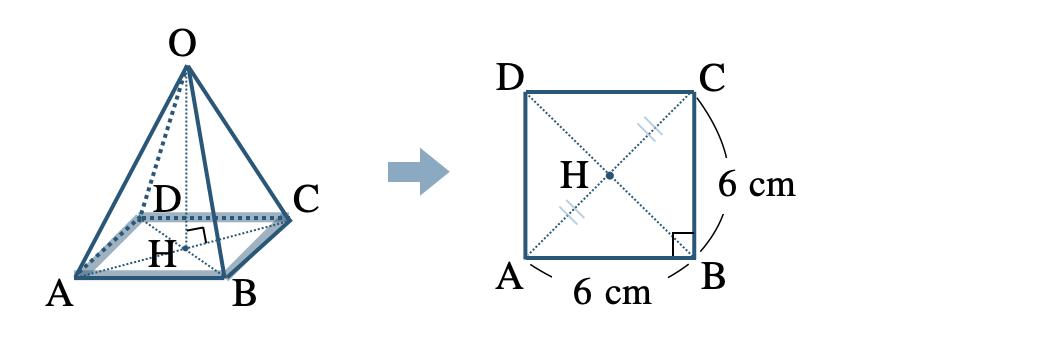
対角線 \({\rm AC}\) の長さは三平方の定理より、
\(\begin{eqnarray}~~~{\rm AC}^2&=&6^2+6^2\\[2pt]~~~&=&36+36\\[2pt]~~~&=&72\end{eqnarray}\)
\({\rm AC}>0\) より、
\(~~~{\rm AC}=\sqrt{72}=\sqrt{6^2{\, \small \times \,}2}=6\sqrt{2}\)
よって、\(\begin{split}{\rm AH}={\frac{\,1\,}{\,2\,}}{\rm AC}\end{split}\) より、
\(\begin{split}~~~{\rm AH}=\frac{\,1\,}{\,2\,}{\, \small \times \,}6\sqrt{2}=3\sqrt{2}\end{split}\)
次に、断面の二等辺三角形 \(\triangle {\rm OAC}\) より、
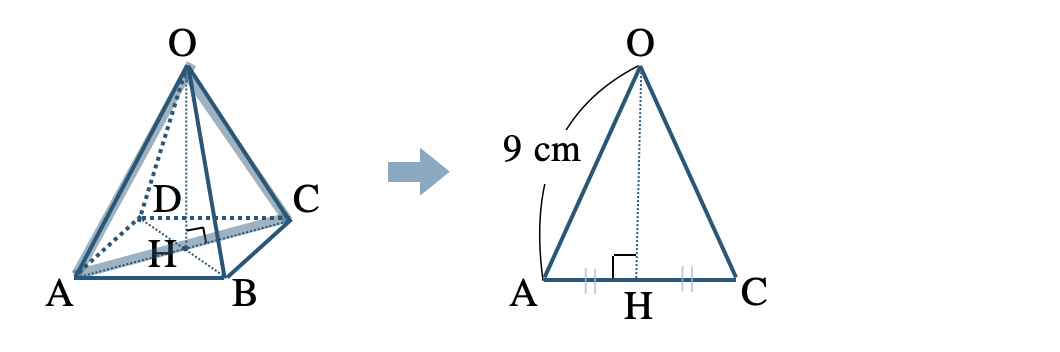
\(\triangle {\rm OAH}\) は直角三角形であるので、三平方の定理より、
\(\begin{eqnarray}~~~{\rm OH}^2+\left(3\sqrt{2}\right)^2&=&9^2\\[2pt]~~~{\rm OH}^2+18&=&81\\[2pt]~~~{\rm OH}^2&=&81-18\\[2pt]~~~{\rm OH}^2&=&63\end{eqnarray}\)
\({\rm OH}>0\) より、
\(~~~{\rm OH}=\sqrt{63}=\sqrt{3^2{\, \small \times \,}7}=3\sqrt{7}\)
よって、正四角錐の高さは \(3\sqrt{7}~{\rm cm}\) となる
また、底面の正方形の面積は \(6{\, \small \times \,}6=36~{\rm cm}^2\)
これより、体積 \({\rm V}~{\rm cm}^3\) は、
\(\begin{split}~~~{\rm V}=\frac{\,1\,}{\,3\,}{\, \small \times \,}36{\, \small \times \,}3\sqrt{7}=36\sqrt{7}\end{split}\)
したがって、答えは
高さ \(3\sqrt{7}~{\rm cm}\)、体積 \(36\sqrt{7}~{\rm cm}^3\)
となる
問題解説(2)
問題
\({\small (2)}~\)次の円錐の高さと体積を求めよ。
次の問いに答えよ。
\({\small (2)}~\)次の円錐の高さと体積を求めよ。

断面の三角形 \(\triangle {\rm ABC}\) について、
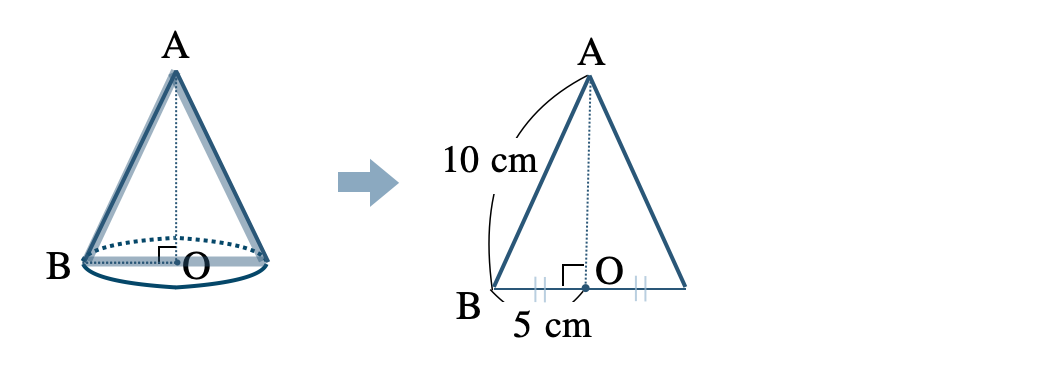
直角三角形であるので、三平方の定理より、
\(\begin{eqnarray}~~~{\rm AO}^2+5^2&=&10^2\\[2pt]~~~{\rm AO}^2+25&=&100\\[2pt]~~~{\rm AO}^2&=&100-25\\[2pt]~~~{\rm AO}^2&=&75\end{eqnarray}\)
\({\rm AO}>0\) より、
\(~~~{\rm AO}=\sqrt{75}=\sqrt{5^2{\, \small \times \,}3}=5\sqrt{3}\)
よって、円錐の高さは \(5\sqrt{3}~{\rm cm}\) となる
底面の円の面積は \(5{\, \small \times \,}5{\, \small \times \,} \pi=25\pi~{\rm cm}^2\)
これより、体積 \({\rm V}~{\rm cm}^3\) は、
\(\begin{split}~~~{\rm V}=\frac{\,1\,}{\,3\,}{\, \small \times \,}25\pi {\, \small \times \,}5\sqrt{3}=\frac{\,125\sqrt{3}\pi\,}{\,3\,}\end{split}\)
したがって、答えは
高さ \(5\sqrt{3}~{\rm cm}\)、体積 \(\begin{split}{\frac{\,125\sqrt{3}\pi\,}{\,3\,}}~{\rm cm}^3\end{split}\)
となる

【問題一覧】中3|三平方の定理
このページは「中学数学3 三平方の定理」の問題一覧ページとなります。解説の見たい単元名がわからないと...


