立体上の最短距離の解法
Point:立体上の最短距離
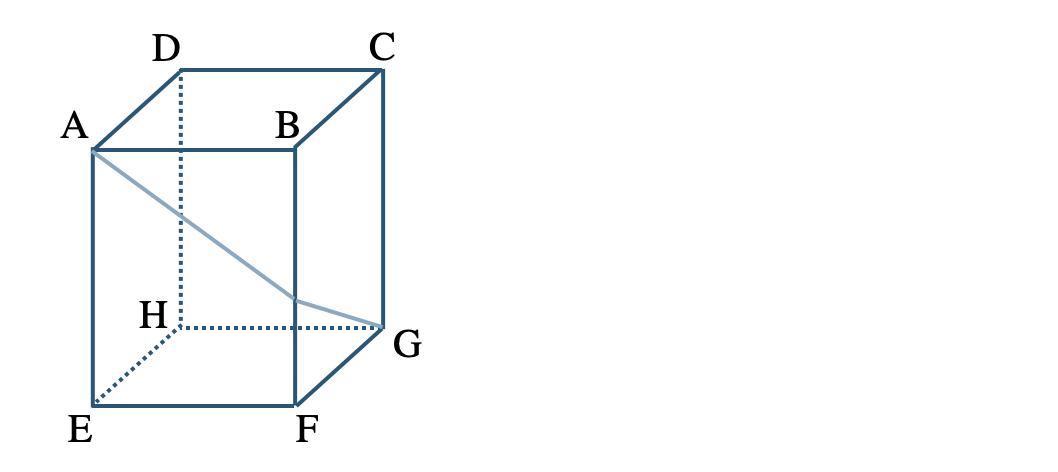

\(\begin{eqnarray}~~~{\rm AE}^2+{\rm EG}^2&=&{\rm AG}^2\\[2pt]~~~{\rm AG}&=&\sqrt{{\rm AE}^2+{\rm EG}^2}\end{eqnarray}\)
立体上の点 \({\rm A}\) から点 \({\rm G}\) までひもをかけるとき、ひもの長さの最短距離は、

① 展開図をかき、点 \({\rm A}\) と点 \({\rm G}\) を結んだ直線をかく。

このとき、線分 \({\rm AG}\) の長さが最短距離となる。
② \(\triangle {\rm AEG}\) が直角三角形となるので、三平方の定理より \({\rm AG}\) の長さを求める。
\(\begin{eqnarray}~~~{\rm AE}^2+{\rm EG}^2&=&{\rm AG}^2\\[2pt]~~~{\rm AG}&=&\sqrt{{\rm AE}^2+{\rm EG}^2}\end{eqnarray}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:立体上の最短距離
問題解説(1)
問題
\({\small (1)}~\)次の図のような1辺が \(6~{\rm cm}\) の立方体において、点 \({\rm A}\) から点 \({\rm G}\) までひもをかけるとき、ひもの長さが最短になる長さを求めよ。
次の問いに答えよ。
\({\small (1)}~\)次の図のような1辺が \(6~{\rm cm}\) の立方体において、点 \({\rm A}\) から点 \({\rm G}\) までひもをかけるとき、ひもの長さが最短になる長さを求めよ。

展開図をかくと、
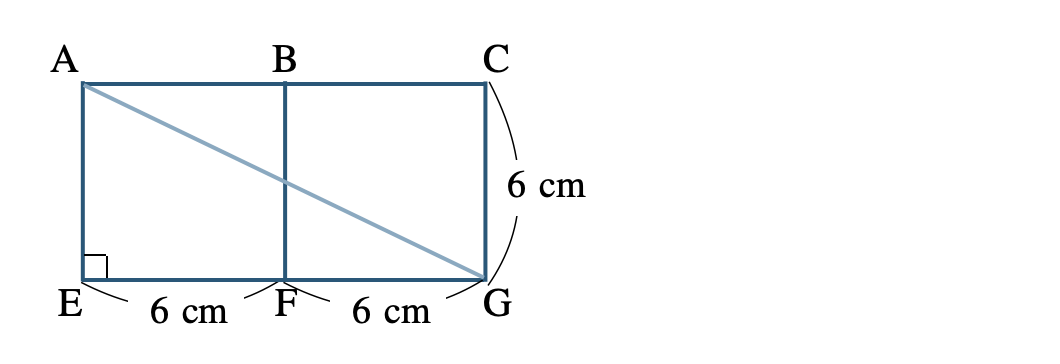
このとき、線分 \({\rm AG}\) の長さが最短距離となる
\({\rm AB}=6~{\rm cm}~,~{\rm BG}=6+6=12~{\rm cm}\) であるので、三平方の定理より、
\(\begin{eqnarray}~~~{\rm AG}^2&=&6^2+12^2\\[2pt]~~~&=&36+144\\[2pt]~~~&=&180\end{eqnarray}\)
\({\rm AG}>0\) より、
\(~~~{\rm AG}=\sqrt{180}=\sqrt{6^2\times5}=6\sqrt{5}\)
したがって、答えは \(6\sqrt{5}~{\rm cm}\) となる
問題解説(2)
問題
\({\small (2)}~\)次の図のような三角柱において、点 \({\rm A}\) から点 \({\rm F}\) までひもをかけるとき、ひもの長さが最短になる長さを求めよ。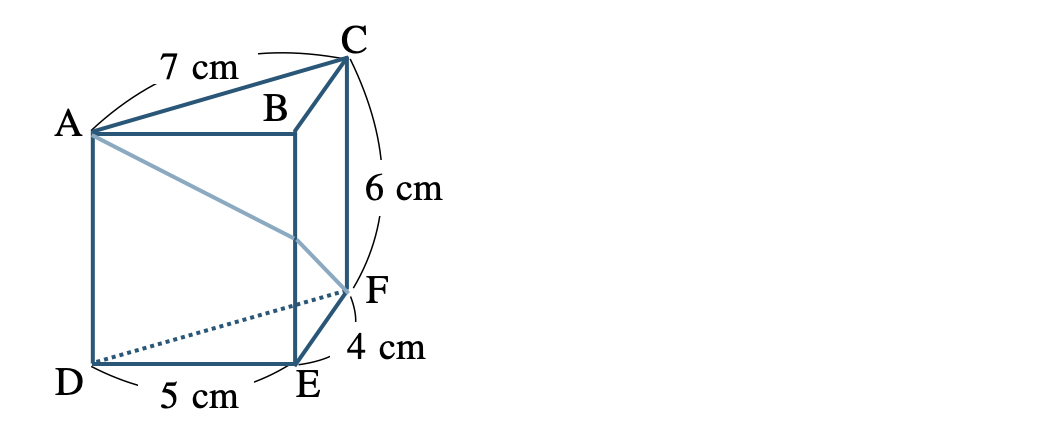
次の問いに答えよ。
\({\small (2)}~\)次の図のような三角柱において、点 \({\rm A}\) から点 \({\rm F}\) までひもをかけるとき、ひもの長さが最短になる長さを求めよ。

展開図をかくと、
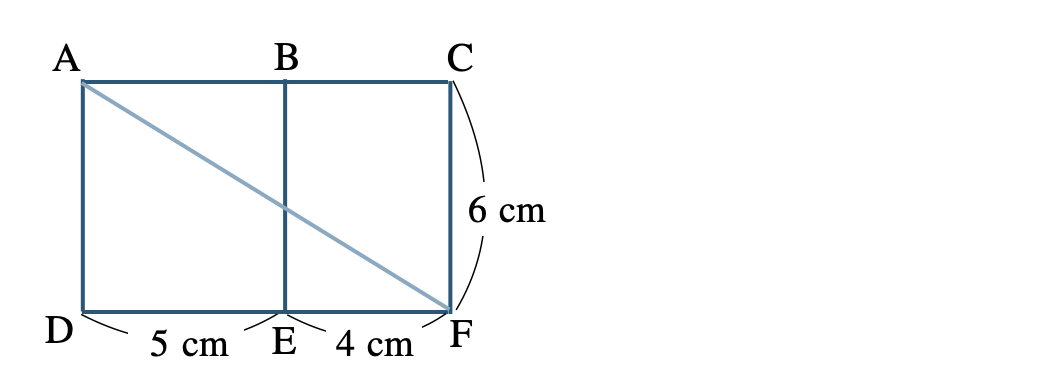
このとき、線分 \({\rm AF}\) の長さが最短距離となる
\({\rm AD}=6~{\rm cm}~,~{\rm DF}=5+4=9~{\rm cm}\) であるので、三平方の定理より、
\(\begin{eqnarray}~~~{\rm AF}^2&=&6^2+9^2\\[2pt]~~~&=&36+81\\[2pt]~~~&=&117\end{eqnarray}\)
\({\rm AF}>0\) より、
\(~~~{\rm AF}=\sqrt{117}=\sqrt{3^2\times13}=3\sqrt{13}\)
したがって、答えは \(3\sqrt{13}~{\rm cm}\) となる

【問題一覧】中3|三平方の定理
このページは「中学数学3 三平方の定理」の問題一覧ページとなります。解説の見たい単元名がわからないと...


