問題:文字式の意味
問題
\({\small (1)}~\)\(n\) を自然数とするとき、次の式はどんな数を表すか答えよ。
① \(2n\) ② \(2n-1\) ③ \(3n\)
\({\small (2)}~\)ある水族館の入場料がおとな1人 \(a\) 円、子ども1人 \(b\) 円のとき、次の式はどんな数を表すか答えよ。
① \(2a+3b~\)円 ② \(a-b~\)円
③ \(0.7a~\)円
\({\small (3)}~\)縦の長さ \(x~({\rm cm})\)、横の長さ \(y~({\rm cm})\) の長方形について、次の式はどんな数を表すか答えよ。
① \(2(x+y)~({\rm cm})\) ② \(xy~({\rm cm}^2)\)
次の問いに答えよ。
\({\small (1)}~\)\(n\) を自然数とするとき、次の式はどんな数を表すか答えよ。
① \(2n\) ② \(2n-1\) ③ \(3n\)
\({\small (2)}~\)ある水族館の入場料がおとな1人 \(a\) 円、子ども1人 \(b\) 円のとき、次の式はどんな数を表すか答えよ。
① \(2a+3b~\)円 ② \(a-b~\)円
③ \(0.7a~\)円
\({\small (3)}~\)縦の長さ \(x~({\rm cm})\)、横の長さ \(y~({\rm cm})\) の長方形について、次の式はどんな数を表すか答えよ。
① \(2(x+y)~({\rm cm})\) ② \(xy~({\rm cm}^2)\)
解法のPoint
Point:整数と文字式の意味
\(n=\{~1~,~2~,~3~,~4~,~\cdots~\}\)
\({\small (1)}~\)偶数(=2の倍数)は \(2n\)
\(2n=\{~2~,~4~,~6~,~8~,~\cdots~\}\)
\({\small (2)}~\)奇数は \(2n-1\)
\(2n-1=\{~1~,~3~,~5~,~7~,~\cdots~\}\)
※ 奇数を \(2n+1\) とすることもあるが、\(n\) が自然数のときは \(3\) 以上の奇数となるので注意。
\({\small (3)}~\)3の倍数は \(3n\)
\(3n=\{~3~,~6~,~9~,~12~,~\cdots~\}\)
\({\small (4)}~\)5の倍数は \(5n\)
\(5n=\{~5~,~10~,~15~,~20~,~\cdots~\}\)
\(n\) を自然数とすると、
\(n=\{~1~,~2~,~3~,~4~,~\cdots~\}\)
\({\small (1)}~\)偶数(=2の倍数)は \(2n\)
\(2n=\{~2~,~4~,~6~,~8~,~\cdots~\}\)
\({\small (2)}~\)奇数は \(2n-1\)
\(2n-1=\{~1~,~3~,~5~,~7~,~\cdots~\}\)
※ 奇数を \(2n+1\) とすることもあるが、\(n\) が自然数のときは \(3\) 以上の奇数となるので注意。
\({\small (3)}~\)3の倍数は \(3n\)
\(3n=\{~3~,~6~,~9~,~12~,~\cdots~\}\)
\({\small (4)}~\)5の倍数は \(5n\)
\(5n=\{~5~,~10~,~15~,~20~,~\cdots~\}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:代金と文字式の意味
\({\small (1)}~\)合計代金
\(5a+2b=5{\, \small \times \,} a+2 {\, \small \times \,} b\)
りんご5個とみかん2個の代金の合計
\({\small (2)}~\)値段の差
\(a-b\)
りんご1個がみかん1個の代金の差
\({\small (3)}~\)割引き
\(\begin{split}0.8a=\frac{\,80\,}{\,100\,}a\end{split}\)
りんご \(a\) 円の \(80 \) %の代金となるので、
りんご1個の \(20 \) %引き=2割引きの代金
りんご1個 \(a\) 円、みかん1個 \(b\) 円とするとき、
\({\small (1)}~\)合計代金
\(5a+2b=5{\, \small \times \,} a+2 {\, \small \times \,} b\)
りんご5個とみかん2個の代金の合計
\({\small (2)}~\)値段の差
\(a-b\)
りんご1個がみかん1個の代金の差
\({\small (3)}~\)割引き
\(\begin{split}0.8a=\frac{\,80\,}{\,100\,}a\end{split}\)
りんご \(a\) 円の \(80 \) %の代金となるので、
りんご1個の \(20 \) %引き=2割引きの代金
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:図形と文字式の意味
\(4x~({\rm cm})=4{\, \small \times \,} x~({\rm cm})\)
1辺の長さの4倍より、正方形の周りの長さ
\(x^2~({\rm cm}^2)=x{\, \small \times \,} x~({\rm cm}^2)\)
辺の長さ × 辺の長さより、正方形の面積
\({\small (2)}~\)半径 \(r~({\rm cm})\) の円
\(2\pi r~({\rm cm})=2{\, \small \times \,} r{\, \small \times \,} \pi~({\rm cm})\)
2 × 半径 × 円周率より、円周の長さ
\(\pi r^2~({\rm cm}^2)=r{\, \small \times \,} r{\, \small \times \,} \pi~({\rm cm}^2)\)
半径 × 半径 × 円周率より、円の面積
\({\small (1)}~\)1辺の長さ \(x~({\rm cm})\) の正方形
\(4x~({\rm cm})=4{\, \small \times \,} x~({\rm cm})\)
1辺の長さの4倍より、正方形の周りの長さ
\(x^2~({\rm cm}^2)=x{\, \small \times \,} x~({\rm cm}^2)\)
辺の長さ × 辺の長さより、正方形の面積
\({\small (2)}~\)半径 \(r~({\rm cm})\) の円
\(2\pi r~({\rm cm})=2{\, \small \times \,} r{\, \small \times \,} \pi~({\rm cm})\)
2 × 半径 × 円周率より、円周の長さ
\(\pi r^2~({\rm cm}^2)=r{\, \small \times \,} r{\, \small \times \,} \pi~({\rm cm}^2)\)
半径 × 半径 × 円周率より、円の面積
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:文字式の意味
問題解説(1)
問題
\({\small (1)}~\)\(n\) を自然数とするとき、次の式はどんな数を表すか答えよ。
① \(2n\) ② \(2n-1\) ③ \(3n\)
次の問いに答えよ。
\({\small (1)}~\)\(n\) を自然数とするとき、次の式はどんな数を表すか答えよ。
① \(2n\) ② \(2n-1\) ③ \(3n\)
① \(2n\)
\(n=\{~1~,~2~,~3~,~4~,~\cdots~\}\)
これより、
\(2n=\{~2~,~4~,~6~,~8~,~\cdots~\}\)
したがって、\(2n\) は2の倍数または偶数となる
② \(2n-1\)
\(n=\{~1~,~2~,~3~,~4~,~\cdots~\}\)
これより、
\(2n-1=\{~1~,~3~,~5~,~7~,~\cdots~\}\)
したがって、\(2n-1\) は奇数となる
③ \(3n\)
\(n=\{~1~,~2~,~3~,~4~,~\cdots~\}\)
これより、
\(3n=\{~3~,~6~,~9~,~12~,~\cdots~\}\)
したがって、\(3n\) は3の倍数となる
問題解説(2)
問題
次の問いに答えよ。
\({\small (2)}~\)ある水族館の入場料がおとな1人 \(a\) 円、子ども1人 \(b\) 円のとき、次の式はどんな数を表すか答えよ。
① \(2a+3b~\)円 ② \(a-b~\)円
③ \(0.7a~\)円
① \(2a+3b~\)円
\(2a+3b=2{\, \small \times \,} a+3{\, \small \times \,} b\)
\(2{\, \small \times \,} a\) はおとな2人分、\(3{\, \small \times \,} b\) は子ども3人分
\(2a+3b\) はこれらの和である
したがって、\(2a+3b\) 円は、
おとな2人と子ども3人の代金の合計 となる
② \(a-b~\)円
おとな1人分 − 子ども1人分である
したがって、\(a-b\) 円は、
おとな1人分が子ども1人分の代金の差 となる
③ \(0.7a~\)円
\(\begin{split}~~~0.7a=\frac{\,70\,}{\,100\,}{\, \small \times \,} a\end{split}\)
おとな1人分 \(a\) 円の代金の \(70 \) %=7割となるので、\(30 \) %引き=3割引きの代金である
したがって、\(0.7a\) は、
おとな1人分の \(30 %\) 引き(3割引き)の代金 となる
問題解説(3)
問題
\({\small (3)}~\)縦の長さ \(x~({\rm cm})\)、横の長さ \(y~({\rm cm})\) の長方形について、次の式はどんな数を表すか答えよ。
① \(2(x+y)~({\rm cm})\) ② \(xy~({\rm cm}^2)\)
次の問いに答えよ。
\({\small (3)}~\)縦の長さ \(x~({\rm cm})\)、横の長さ \(y~({\rm cm})\) の長方形について、次の式はどんな数を表すか答えよ。
① \(2(x+y)~({\rm cm})\) ② \(xy~({\rm cm}^2)\)
① \(2(x+y)~({\rm cm})\)
\(~~~2(x+y)=2{\, \small \times \,} (x+y)\)
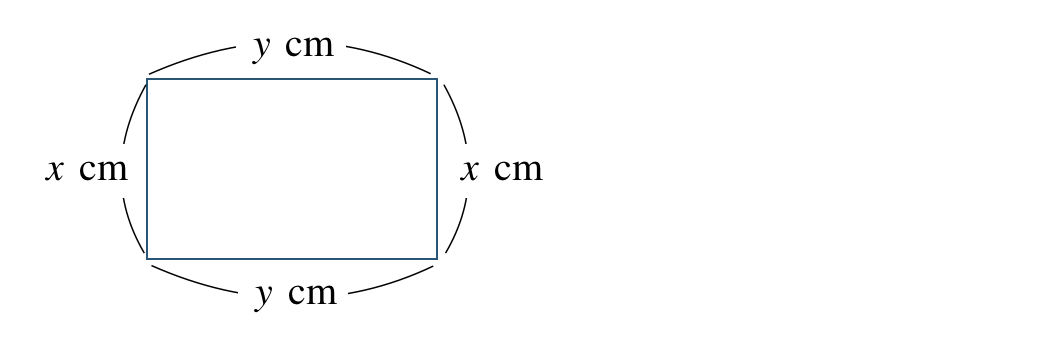
\(x+y\) はこの長方形の縦の長さと横の長さの和であり、\(2(x+y)\) はこの長さの2倍である
したがって、\(2(x+y)\) は、
長方形の周りの長さ となる
② \(xy~({\rm cm}^2)\)
\(~~~xy=x{\, \small \times \,} y\)
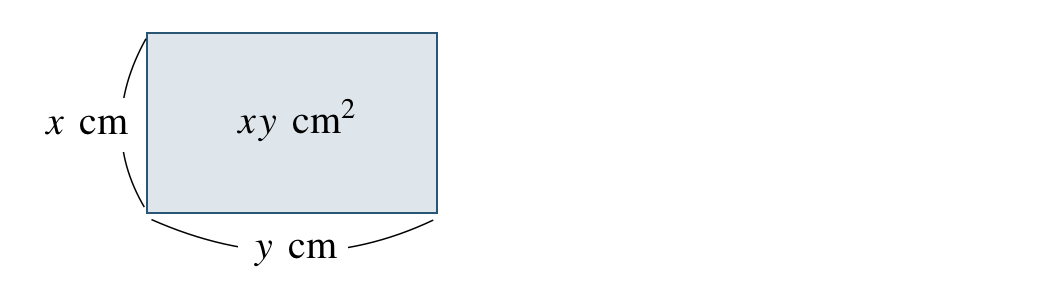
\(x{\, \small \times \,} y\) はこの長方形は、縦の長さ×横の長さより、面積である
したがって、\(xy\) は 長方形の面積 となる

【問題一覧】中1|文字式
このページは「中学数学1 文字式」の問題一覧ページとなります。解説の見たい単元名がわからないときは、...


