問題:等しい関係を表す式
問題
\({\small (1)}~\)1個 \(70\) 円のみかんを \(x\) 個と1個 \(120\) 円のりんごを \(y\) 個を買ったときの代金の合計が \(1000\) 円であった。
\({\small (2)}~\)\(100~({\rm cm})\) のひもから \(a~({\rm cm})\) のひもを3本切りとったときの残りが \(b~({\rm cm})\) であった。
\({\small (3)}~\)\(x~({\rm kg})\) の \(12\) %の重さが \(y~({\rm kg})\) であった。
\({\small (4)}~\)\(a\) 個のアメを \(b\) 人の子どもに1人3個ずつ分けるとき2個足りなかった。
\({\small (5)}~\)\(500~({\rm m})\) の道のりを分速 \(x~({\rm m})\) で \(10\) 分走ったときの残りの道のりが \(y~({\rm m})\) であった。
次の数量の関係を等式で表す。
\({\small (1)}~\)1個 \(70\) 円のみかんを \(x\) 個と1個 \(120\) 円のりんごを \(y\) 個を買ったときの代金の合計が \(1000\) 円であった。
\({\small (2)}~\)\(100~({\rm cm})\) のひもから \(a~({\rm cm})\) のひもを3本切りとったときの残りが \(b~({\rm cm})\) であった。
\({\small (3)}~\)\(x~({\rm kg})\) の \(12\) %の重さが \(y~({\rm kg})\) であった。
\({\small (4)}~\)\(a\) 個のアメを \(b\) 人の子どもに1人3個ずつ分けるとき2個足りなかった。
\({\small (5)}~\)\(500~({\rm m})\) の道のりを分速 \(x~({\rm m})\) で \(10\) 分走ったときの残りの道のりが \(y~({\rm m})\) であった。
解法のPoint
Point:等しい関係を表す式
等式 \(2x+3=12\) について、
\(2x+3\) を左辺、\(12\) を右辺、\(=\) を等号、
左辺と右辺を合わせて「両辺」という。
■ 数量の関係を等式で表す
\(x\) を \(2\) 倍して \(+3\) した数は \(12\) に等しい。
① 問題文より、同じ数量を表す2つの式をそれぞれつくる。
\(x\) を \(2\) 倍して \(+3\) した数は \(2x+3\)
② この2つの式を等号=でつなぐ。
\(12\) に等しいので、等式 \(2x+3=12\)
数量が等しい関係を等号=(イコール)を使って表す式を「等式」という。
等式 \(2x+3=12\) について、
\(2x+3\) を左辺、\(12\) を右辺、\(=\) を等号、
左辺と右辺を合わせて「両辺」という。
■ 数量の関係を等式で表す
\(x\) を \(2\) 倍して \(+3\) した数は \(12\) に等しい。
① 問題文より、同じ数量を表す2つの式をそれぞれつくる。
\(x\) を \(2\) 倍して \(+3\) した数は \(2x+3\)
② この2つの式を等号=でつなぐ。
\(12\) に等しいので、等式 \(2x+3=12\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:等しい関係を表す式
問題解説(1)
問題
\({\small (1)}~\)1個 \(70\) 円のみかんを \(x\) 個と1個 \(120\) 円のりんごを \(y\) 個を買ったときの代金の合計が \(1000\) 円であった。
次の数量の関係を等式で表す。
\({\small (1)}~\)1個 \(70\) 円のみかんを \(x\) 個と1個 \(120\) 円のりんごを \(y\) 個を買ったときの代金の合計が \(1000\) 円であった。
図で表すと、
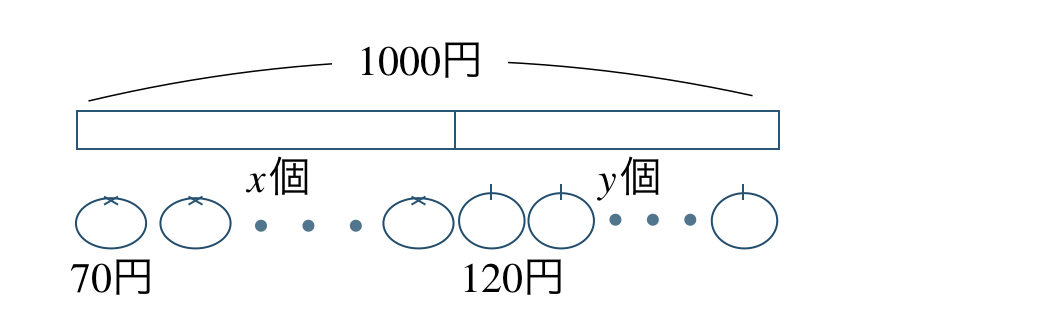
1個 \(70\) 円のみかんを \(x\) 個と1個 \(120\) 円のりんごを \(y\) 個買ったときの代金の合計は、
\(\begin{split}~~~70{\, \small \times \,} x+120{\, \small \times \,} y=70x+120y\end{split}\)
これが \(1000\) 円と等しいので、
答えは、
\(\begin{split}~~~70x+120y=1000\end{split}\)となる
問題解説(2)
問題
\({\small (2)}~\)\(100~({\rm cm})\) のひもから \(a~({\rm cm})\) のひもを3本切りとったときの残りが \(b~({\rm cm})\) であった。
次の数量の関係を等式で表す。
\({\small (2)}~\)\(100~({\rm cm})\) のひもから \(a~({\rm cm})\) のひもを3本切りとったときの残りが \(b~({\rm cm})\) であった。
図で表すと、

\(100~({\rm cm})\) のひもから \(a~({\rm cm})\) のひもを3本切りとったときの残りは、
\(\begin{split}~~~100-3{\, \small \times \,} a=100-3a\end{split}\)
これが \(b~({\rm cm})\) と等しいので、
答えは、
\(\begin{split}~~~100-3a=b\end{split}\)となる
【別解】
図で表すと、

\(a~({\rm cm})\) のひもを3本切りとったときの長さは、
\(\begin{split}~~~a{\, \small \times \,} 3=3a\end{split}\)
全体のひもの長さで式をつくると、
答えは
\(\begin{split}~~~100=3a+b\end{split}\)となる
問題解説(3)
問題
\({\small (3)}~\)\(x~({\rm kg})\) の \(12\) %の重さが \(y~({\rm kg})\) であった。
次の数量の関係を等式で表す。
\({\small (3)}~\)\(x~({\rm kg})\) の \(12\) %の重さが \(y~({\rm kg})\) であった。
図で表すと、

\(x~({\rm kg})\) の \(12\) %は、
\(\begin{split}~~~x{\, \small \times \,}\frac{\,12\,}{\,100\,}=\frac{\,3\,}{\,25\,}x\end{split}\)
これが \(y~({\rm kg})\) と等しいので、
答えは、
\(\begin{split}~~~\frac{\,3\,}{\,25\,}x=y\end{split}\)
となる
問題解説(4)
問題
\({\small (4)}~\)\(a\) 個のアメを \(b\) 人の子どもに1人3個ずつ分けるとき2個足りなかった。
次の数量の関係を等式で表す。
\({\small (4)}~\)\(a\) 個のアメを \(b\) 人の子どもに1人3個ずつ分けるとき2個足りなかった。
図で表すと、
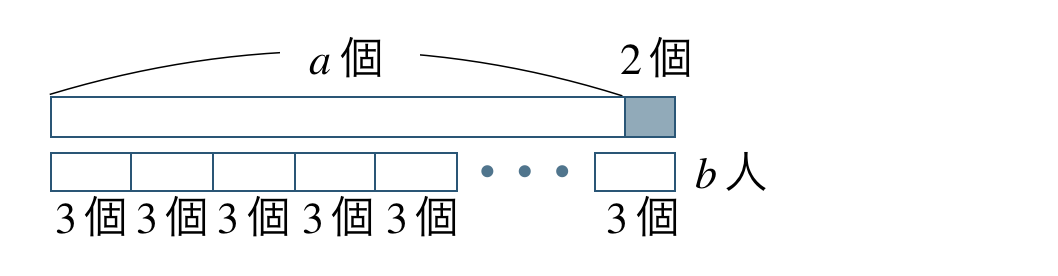
\(b\) 人の子どもに1人3個ずつ分けると、
\(\begin{split}~~~b{\, \small \times \,}3=3b\end{split}\)
\(a\) 個では2個足りないので、\(3b\) から \(a\) を引いた数が \(2\) となる
したがって、答えは
\(\begin{split}~~~3b-a=2\end{split}\)となる
【別解】
図で表すと、

\(b\) 人の子どもに1人3個ずつ分けると、
\(\begin{split}~~~b{\, \small \times \,}3=3b\end{split}\)
\(a\) 個では2個足りないので、アメの合計で式をつくると、
答えは
\(\begin{split}~~~a+2=3b\end{split}\)となる
問題解説(5)
問題
\({\small (5)}~\)\(500~({\rm m})\) の道のりを分速 \(x~({\rm m})\) で \(10\) 分走ったときの残りの道のりが \(y~({\rm m})\) であった。
次の数量の関係を等式で表す。
\({\small (5)}~\)\(500~({\rm m})\) の道のりを分速 \(x~({\rm m})\) で \(10\) 分走ったときの残りの道のりが \(y~({\rm m})\) であった。
図で表すと、
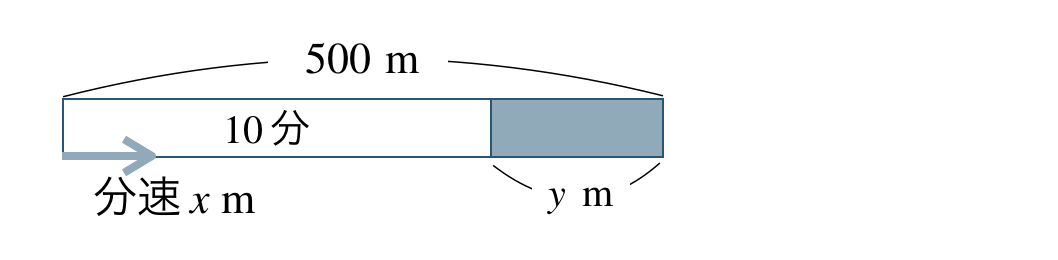
分速 \(x~({\rm m})\) で \(10\) 分走った道のりは、
\(\begin{split}~~~x{\, \small \times \,} 10=10x~({\rm m})\end{split}\)
\(500~({\rm m})\) の道のりを走ったときの残りの道のりが \(y~({\rm m})\) であるので、
答えは
\(\begin{split}~~~500-10x=y\end{split}\)となる
【別解】
図で表すと、

分速 \(x~({\rm m})\) で \(10\) 分走った道のりは、
\(\begin{split}~~~x{\, \small \times \,} 10=10x~({\rm m})\end{split}\)
全体の道のりで式をつくると、
答えは
\(\begin{split}~~~500=10x+y\end{split}\)となる

【問題一覧】中1|文字式
このページは「中学数学1 文字式」の問題一覧ページとなります。解説の見たい単元名がわからないときは、...


