問題:垂線の作図
次の問いに答えよ。
\({\small (1)}\)点 \({\rm P}\) を通る直線 \(l\) の垂線を作図せよ。
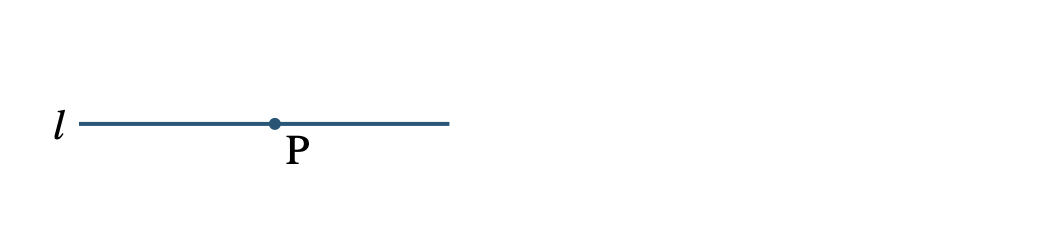
\({\small (2)}~\)点 \({\rm Q}\) を通る直線 \(l\) の垂線を作図せよ。
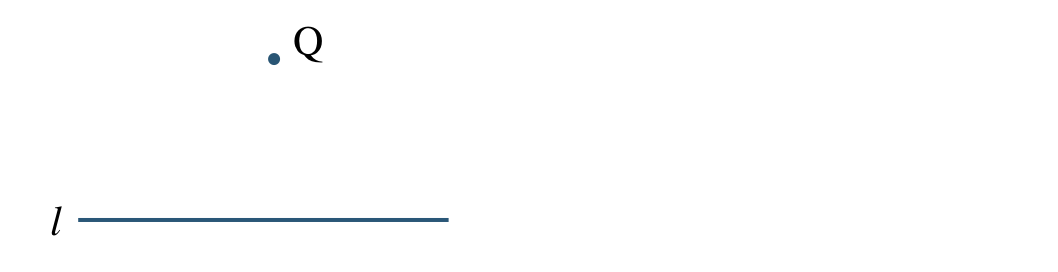
解法のPoint
直線 \(l\) 上の点 \({\rm P}\) を通る直線 \(l\) の垂線の作図は、

① コンパスで点 \({\rm P}\) を中心とする円をかき、直線 \(l\) との交点を \({\rm A~,~B}\) とする。
② コンパスで2点 \({\rm A~,~B}\) をそれぞれ中心として、同じ半径の円をかき、その2つの円の交点を \({\rm C~,~D}\) とする。
※ 線分 \({\rm AB}\) の垂直二等分線の作図
③ 直線 \({\rm CD}\) をひくと、点 \({\rm P}\) を通る垂線となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
直線 \(l\) 上にない点 \({\rm P}\) を通る直線 \(l\) の垂線の作図は、
【パターン1】
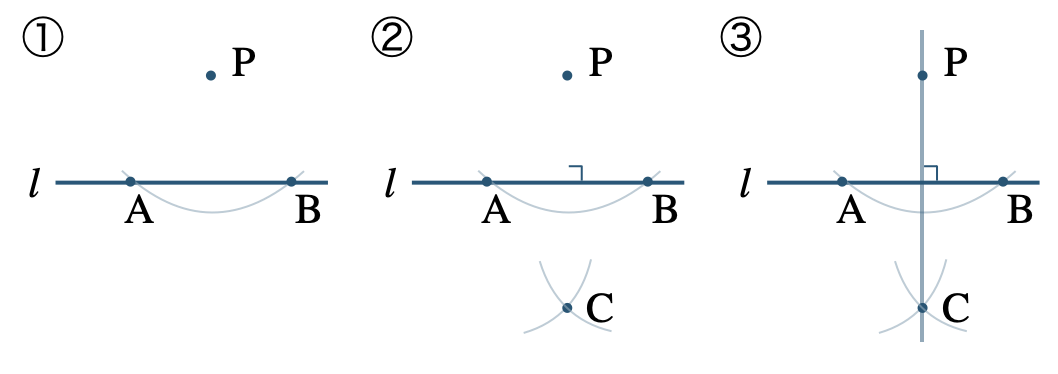
① コンパスで点 \({\rm P}\) を中心とする円をかき、直線 \(l\) との交点を \({\rm A~,~B}\) とする。
② コンパスで2点 \({\rm A~,~B}\) をそれぞれ中心として、半径 \({\rm PA(=PB)}\) の円をかき、その2つの円の交点を \({\rm D}\) とする。
③ 直線 \({\rm PC}\) をひくと、点 \({\rm P}\) を通る垂線となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
直線 \(l\) 上にない点 \({\rm P}\) を通る直線 \(l\) の垂線の作図は、
【パターン2】
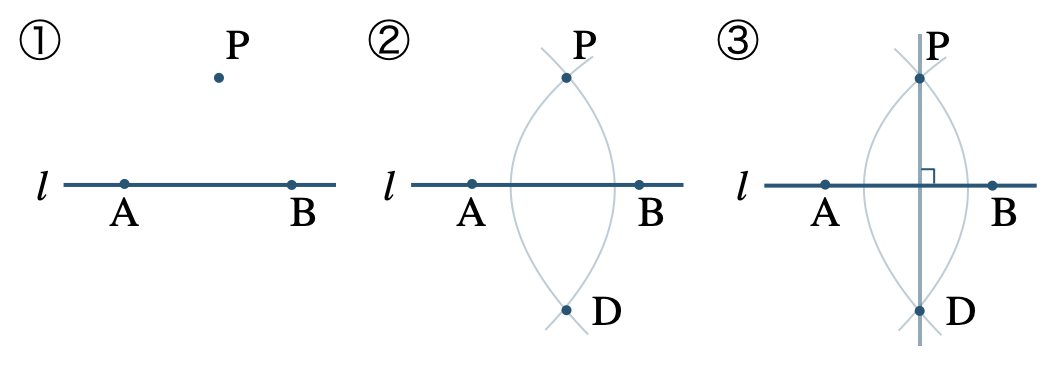
① 直線 \(l\) 上に2点 \({\rm A~,~B}\) をとる。
※ どこでもよい。
② コンパスで点 \({\rm A}\) を中心として、半径 \({\rm AP}\) の円をかき、点 \({\rm B}\) を中心として、半径 \({\rm BP}\) の円をかく。
③ 2つの円の交点を \({\rm D}\) として、直線 \({\rm PD}\) をひくと、点 \({\rm D}\) を通る垂線となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:垂線の作図
問題解説(1)
次の問いに答えよ。
\({\small (1)}\)点 \({\rm P}\) を通る直線 \(l\) の垂線を作図せよ。
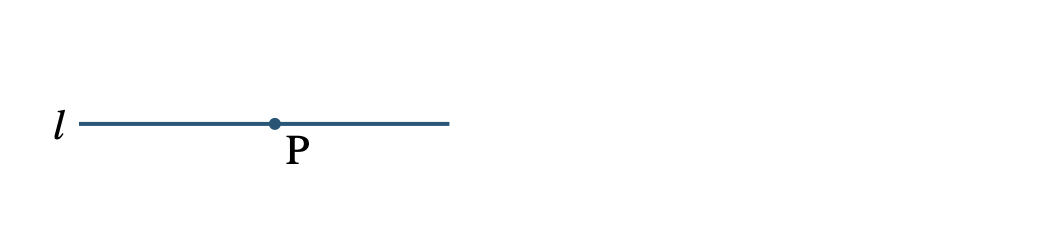
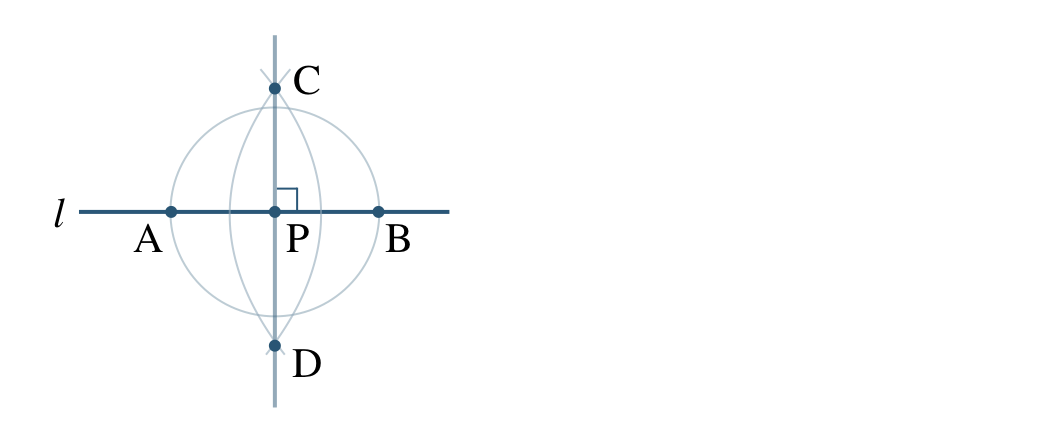
コンパスで点 \({\rm P}\) を中心とする円をかき、直線 \(l\) との交点を \({\rm A~,~B}\) とする
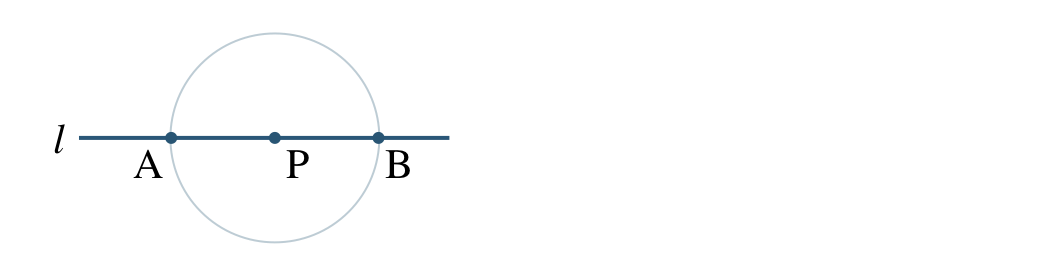
コンパスで2点 \({\rm A~,~B}\) をそれぞれ中心として、同じ半径の円をかき、その2つの円の交点を \({\rm C~,~D}\) とする
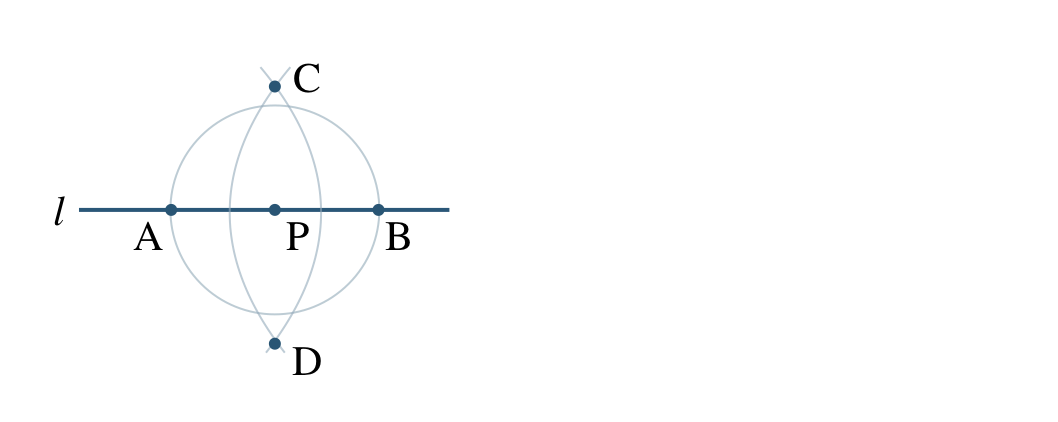
直線 \({\rm CD}\) をひくと、点 \({\rm P}\) を通る垂線となる
問題解説(2)
次の問いに答えよ。
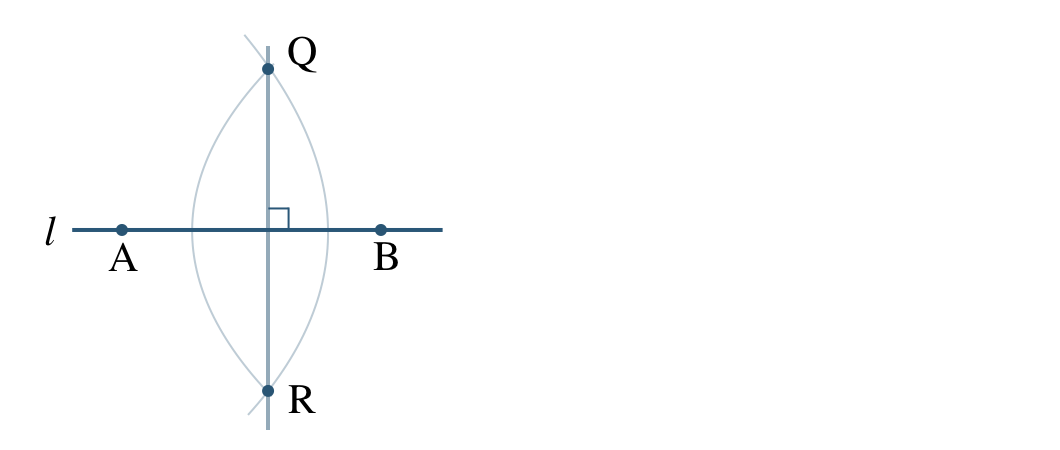
\({\small (2)}~\)点 \({\rm Q}\) を通る直線 \(l\) の垂線を作図せよ。
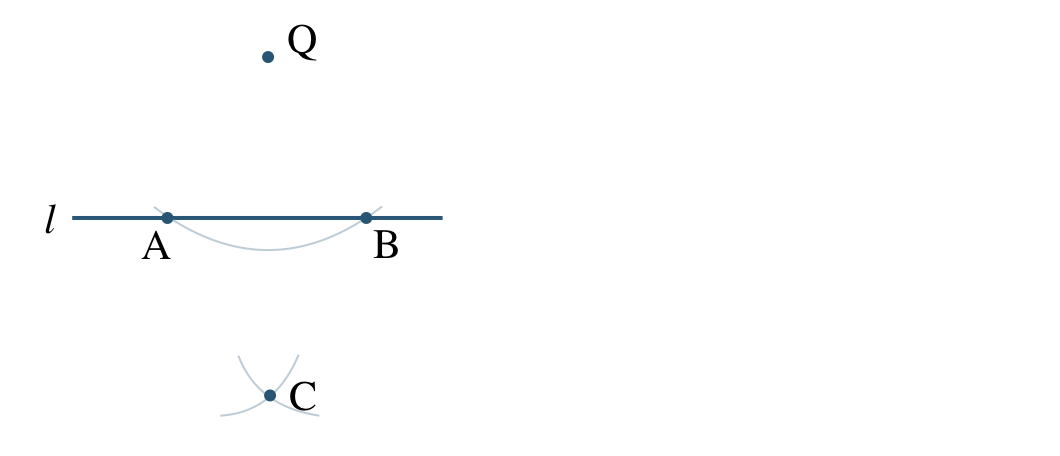
コンパスで点 \({\rm Q}\) を中心とする円をかき、直線 \(l\) との交点を \({\rm A~,~B}\) とする

コンパスで2点 \({\rm A~,~B}\) をそれぞれ中心として、半径 \({\rm QA(=QB)}\) の円をかき、その2つの円の交点を \({\rm C}\) とする
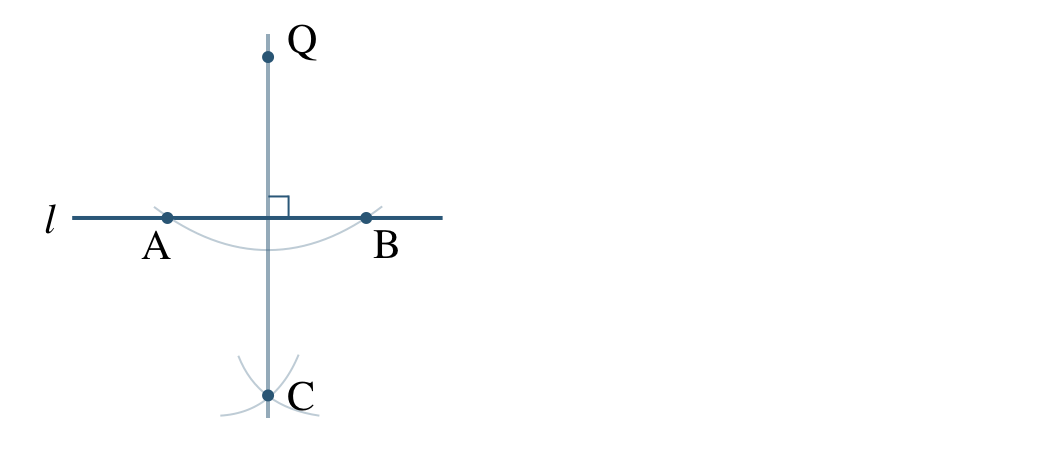
直線 \({\rm QC}\) をひくと、点 \({\rm Q}\) を通る垂線となる
【別解】
直線 \(l\) 上に2点 \({\rm A~,~B}\) をとる
(※ どこでもよい。)
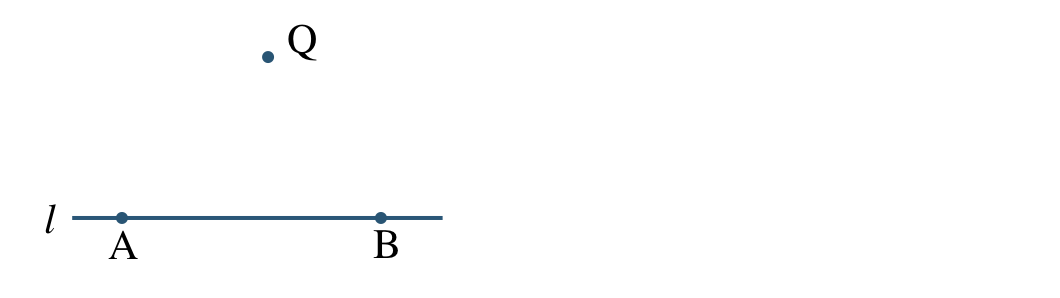
コンパスで点 \({\rm A}\) を中心として、半径 \({\rm AQ}\) の円をかく
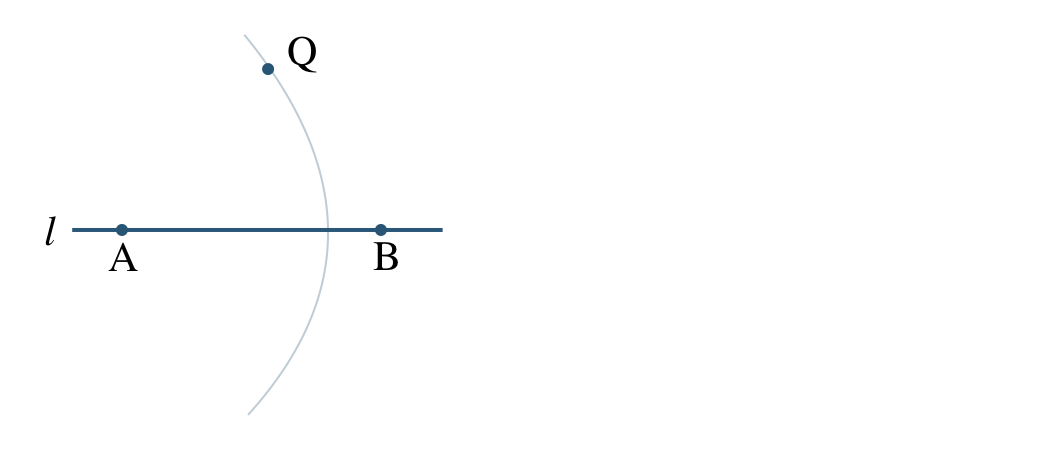
コンパスで点 \({\rm B}\) を中心として、半径 \({\rm BQ}\) の円をかく
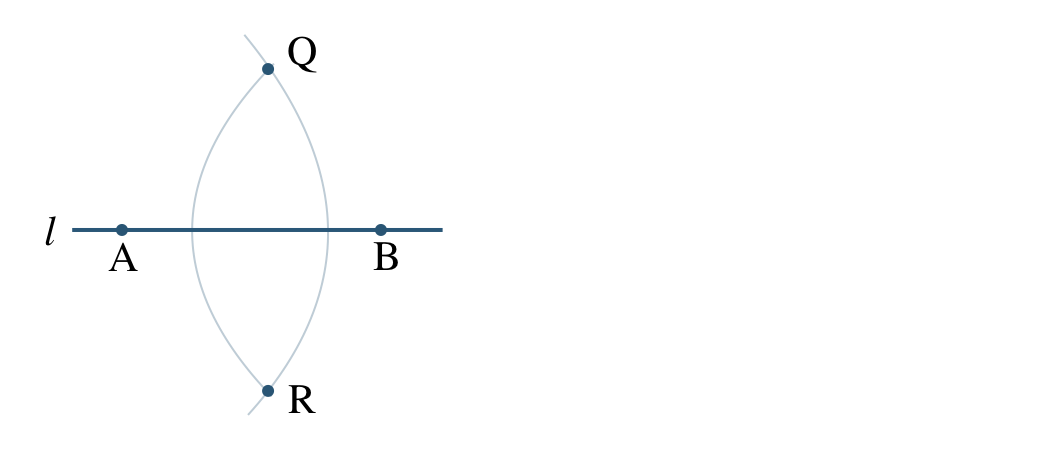
2つの円の交点を \({\rm R}\) として、直線 \({\rm QR}\) をひくと、点 \({\rm Q}\) を通る垂線となる