問題:二等辺三角形の証明
問題
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\)
であることを、\(\angle {\rm A}\) の二等分線をひくことで証明せよ。
\({\small (2)}~\)\({\rm AB=AC}\) の二等辺三角形 \(\triangle {\rm ABC}\) において、\(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とすると、\({\rm AD\perp BC}\) であることを証明せよ。
\({\small (3)}~\)次の図において、\({\rm AB=AC~,~BD=CD}\) であるとき、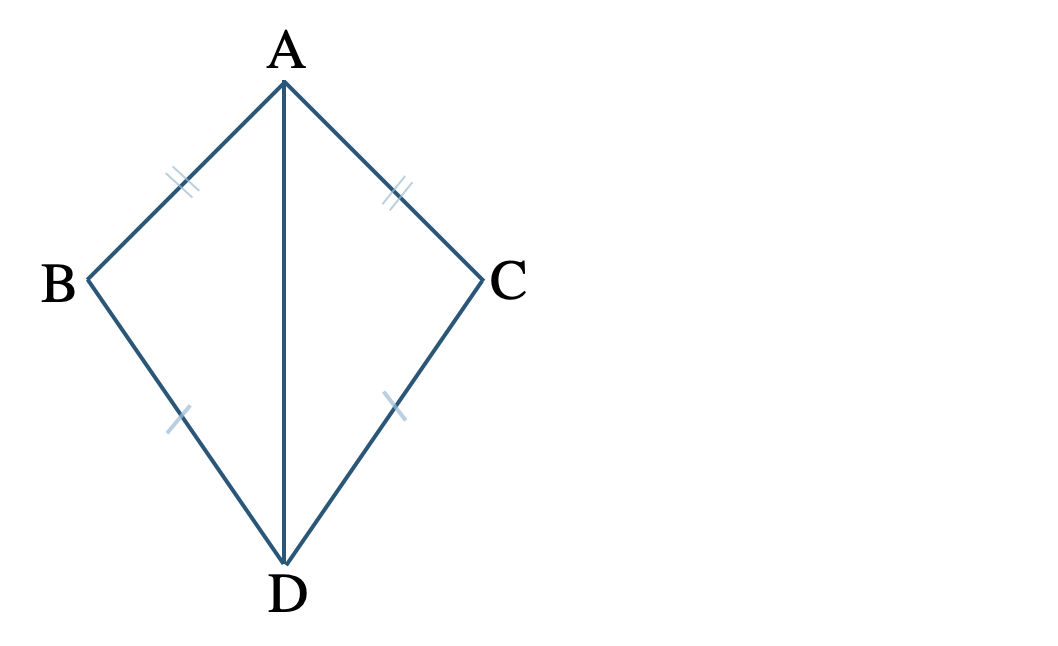
次の証明をせよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\)
であることを、\(\angle {\rm A}\) の二等分線をひくことで証明せよ。
\({\small (2)}~\)\({\rm AB=AC}\) の二等辺三角形 \(\triangle {\rm ABC}\) において、\(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とすると、\({\rm AD\perp BC}\) であることを証明せよ。
\({\small (3)}~\)次の図において、\({\rm AB=AC~,~BD=CD}\) であるとき、

\(\angle{\rm BAD}=\angle{\rm CAD}\) であることを証明せよ。
解法のPoint
Point:二等辺三角形の証明
\(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) として、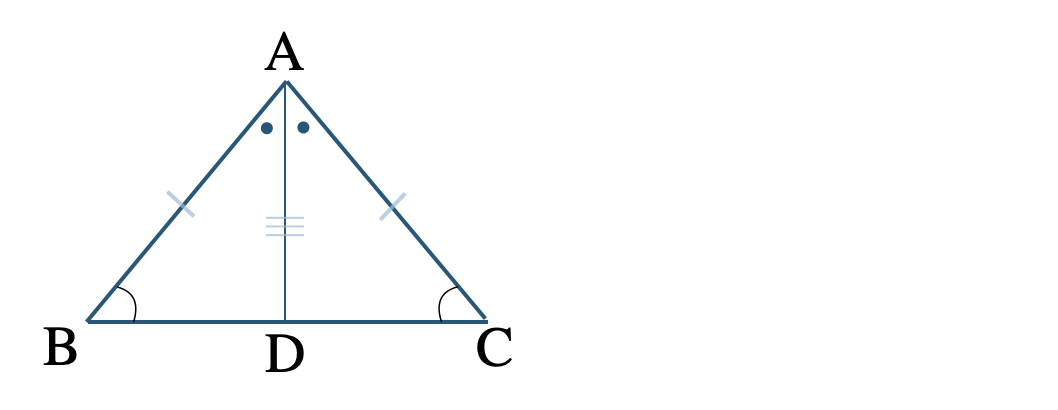
\(\angle{\rm B}=\angle{\rm C}\) を証明するために、
\(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) に着目する。
② 二等辺三角形の定義 \({\rm AB=AC}\) などから、この2つの三角形が合同であることを証明する。
③ 合同な図形の性質より、証明することがらを示す。
\(\triangle {\rm ABC}\) において、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\) の証明方法は、
\(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) として、

① 証明することがらをふくむ2つの三角形に着目する。
\(\angle{\rm B}=\angle{\rm C}\) を証明するために、
\(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) に着目する。
② 二等辺三角形の定義 \({\rm AB=AC}\) などから、この2つの三角形が合同であることを証明する。
③ 合同な図形の性質より、証明することがらを示す。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:二等辺三角形の証明
問題解説(1)
問題
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\)
であることを、\(\angle {\rm A}\) の二等分線をひくことで証明せよ。
次の証明をせよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\)
であることを、\(\angle {\rm A}\) の二等分線をひくことで証明せよ。

\(\angle{\rm B}=\angle{\rm C}\) を示すために、2つの三角形 \(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) に着目する。
[証明] \(\angle{\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とする
\(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) について、
仮定より、
\(~~~{\rm AB=AC}~~~\cdots{\large ①}\)
線分 \({\rm AD}\) は \(\angle{\rm A}\) の二等分するので、
\(~~~\angle{\rm BAD}=\angle{\rm CAD}~~~\cdots{\large ②}\)
また、共通の辺より、
\(~~~{\rm AD=AD}~~~\cdots{\large ③}\)
①、②、③より、2組の辺とその間の角がそれぞれ等しいので、
\(~~~\triangle {\rm ABD}\equiv\triangle {\rm ACD}\)
合同な図形では、対応する角が等しいから、
\(~~~\angle{\rm ABD}=\angle{\rm ACD}\)
よって、
\(~~~\angle{\rm B}=\angle{\rm C}\)
したがって、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\)
となる [終]
※ これより、二等辺三角形の定理である「二等辺三角形の底角が等しい。」が示される。
問題解説(2)
問題
\({\small (2)}~\)\({\rm AB=AC}\) の二等辺三角形 \(\triangle {\rm ABC}\) において、\(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とすると、\({\rm AD\perp BC}\) であることを証明せよ。
次の証明をせよ。
\({\small (2)}~\)\({\rm AB=AC}\) の二等辺三角形 \(\triangle {\rm ABC}\) において、\(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とすると、\({\rm AD\perp BC}\) であることを証明せよ。
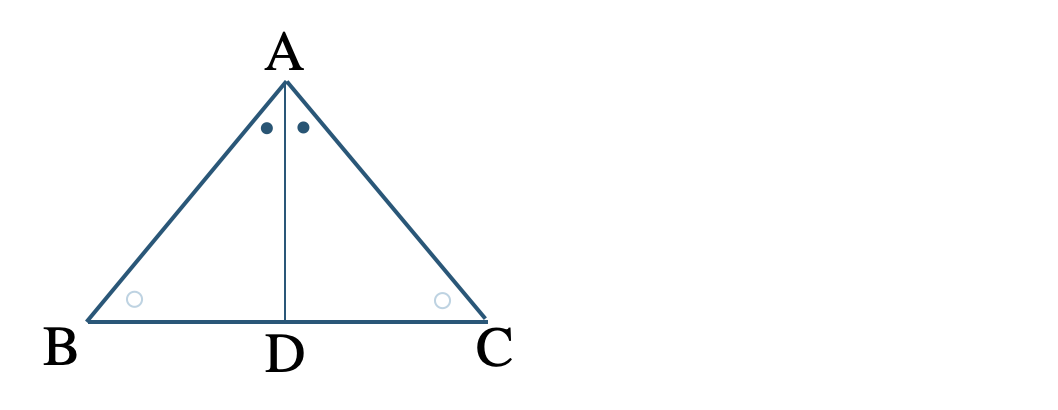
(1)より、\(\triangle {\rm ABD}\equiv\triangle {\rm ACD}\) であり、\(\angle{\rm ADB}+\angle{\rm ADC}=180^\circ\) を使う。
[証明] (1)より、\(\triangle {\rm ABD}\equiv\triangle {\rm ACD}\) であり、合同な図形では、対応する角が等しいから、
\(~~~\angle{\rm ADB}=\angle{\rm ADC}~~~\cdots{\large ①}\)
また、
\(~~~\angle{\rm ADB}+\angle{\rm ADC}=180^\circ~~~\cdots{\large ②}\)
①を代入すると、
\(\begin{eqnarray}~~~\angle{\rm ADB}+\angle{\rm ADC}&=&180^\circ\\[2pt]~~~2\angle{\rm ADB}&=&180^\circ\\[2pt]~~~\angle{\rm ADB}&=&90^\circ\end{eqnarray}\)
したがって、\({\rm AD\perp BC}\) [終]
問題解説(3)
問題
\({\small (3)}~\)次の図において、\({\rm AB=AC~,~BD=CD}\) であるとき、
次の証明をせよ。
\({\small (3)}~\)次の図において、\({\rm AB=AC~,~BD=CD}\) であるとき、

\(\angle{\rm BAD}=\angle{\rm CAD}\) であることを証明せよ。
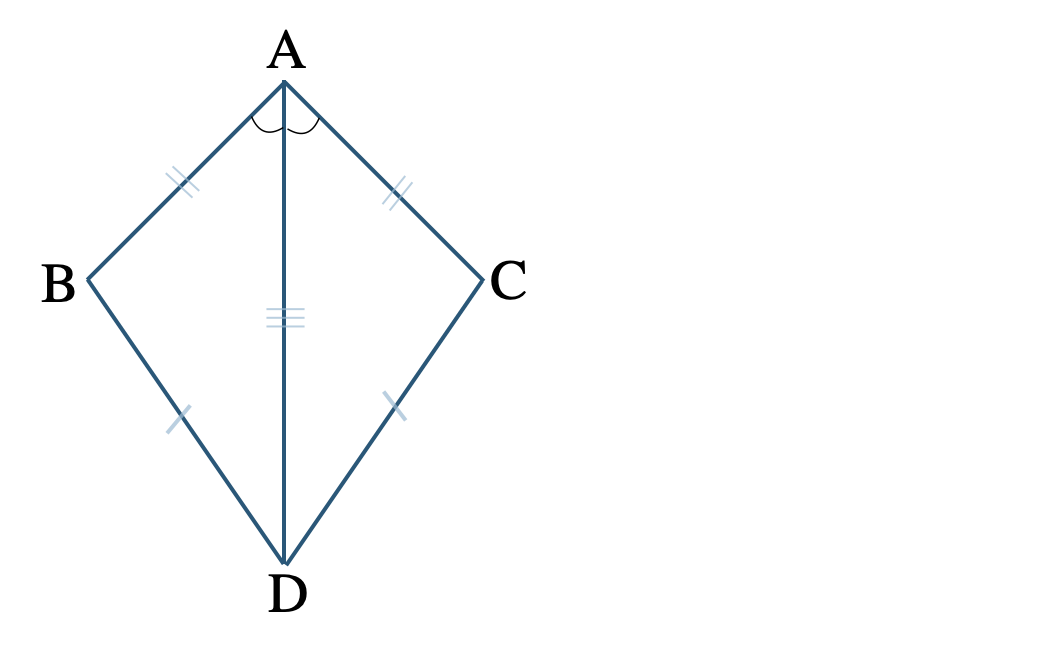
\(\angle{\rm BAD}=\angle{\rm CAD}\) を示すために、2つの三角形 \(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) に着目する。
[証明] \(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) について、
仮定より、
\(~~~{\rm AB=AC}~~~\cdots{\large ①}\)
\(~~~{\rm BD=CD}~~~\cdots{\large ②}\)
また、共通の辺より、
\(~~~{\rm AD=AD}~~~\cdots{\large ③}\)
①、②、③より、3組の辺がそれぞれ等しいので、
\(~~~\triangle {\rm ABD}\equiv\triangle {\rm ACD}\)
合同な図形では、対応する角が等しいから、
\(~~~\angle{\rm BAD}=\angle{\rm CAD}\)
[終]
※ (2)と(3)より、二等辺三角形の定理である「二等辺三角形の頂角の二等分線は、底角を垂直に二等分する。」が示される。

【問題一覧】中2|三角形と四角形
このページは「中学数学2 三角形と四角形」の問題一覧ページとなります。解説の見たい単元名がわからない...


