問題:正三角形の性質
問題
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\({\rm AB=BC=CA}\)
ならば \(\angle{\rm A}=\angle{\rm B}=\angle{\rm C}\)
であることを証明せよ。
\({\small (2)}~\)3つの角がすべて等しい \(\triangle {\rm ABC}\) は正三角形であることを証明せよ。
次の証明をせよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\({\rm AB=BC=CA}\)
ならば \(\angle{\rm A}=\angle{\rm B}=\angle{\rm C}\)
であることを証明せよ。
\({\small (2)}~\)3つの角がすべて等しい \(\triangle {\rm ABC}\) は正三角形であることを証明せよ。
解法のPoint
Point:正三角形の性質
【定義】3つの辺がすべて等しい三角形を正三角形という。
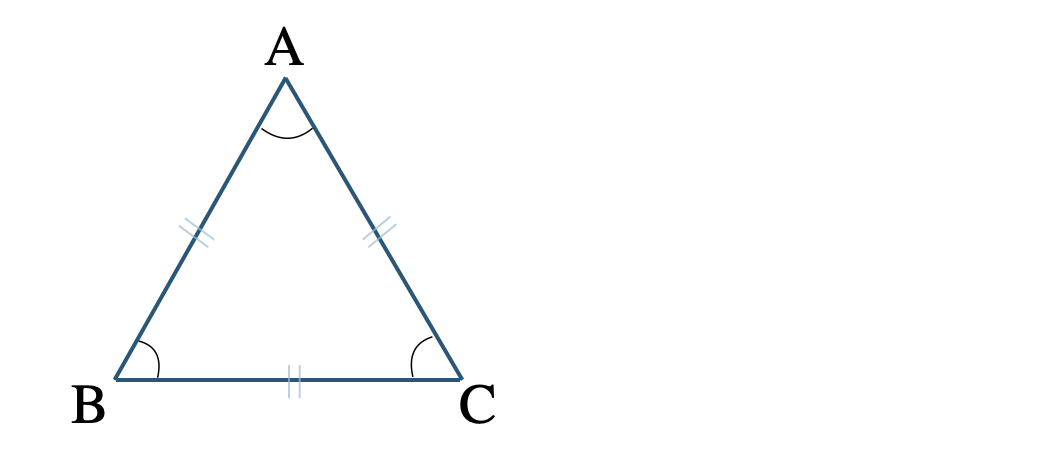
【定理】正三角形の3つの角はすべて等しい。
正三角形の定義は、
【定義】3つの辺がすべて等しい三角形を正三角形という。

正三角形の定理は、
【定理】正三角形の3つの角はすべて等しい。
→ 上の図で、\(\angle{\rm A}=\angle{\rm B}=\angle{\rm C}=60^\circ\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:正三角形の性質
問題解説(1)
問題
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\({\rm AB=BC=CA}\)
ならば \(\angle{\rm A}=\angle{\rm B}=\angle{\rm C}\)
であることを証明せよ。
次の証明をせよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\({\rm AB=BC=CA}\)
ならば \(\angle{\rm A}=\angle{\rm B}=\angle{\rm C}\)
であることを証明せよ。
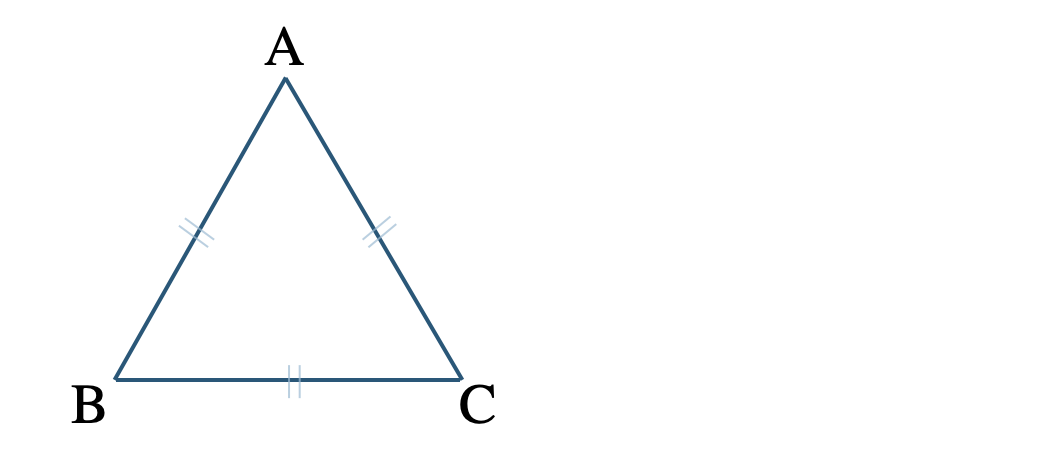
三角形の3つの角が等しいことを示すために、二等辺三角形の性質を2回使う。
[証明] \(\triangle {\rm ABC}\) において、
\({\rm AB=AC}\) より、\(\angle{\rm A}\) を頂角とする二等辺三角形となる
よって、底角が等しいので、
\(~~~\angle{\rm B}=\angle{\rm C}~~~\cdots{\large ①}\)
また、\({\rm BA=BC}\) より、\(\angle{\rm B}\) を頂角とする二等辺三角形となる
よって、底角が等しいので、
\(~~~\angle{\rm A}=\angle{\rm C}~~~\cdots{\large ②}\)
したがって、①と②より、
\(~~~\angle{\rm A}=\angle{\rm B}=\angle{\rm C}\)
[終]
問題解説(2)
問題
\({\small (2)}~\)3つの角がすべて等しい \(\triangle {\rm ABC}\) は正三角形であることを証明せよ。
次の証明をせよ。
\({\small (2)}~\)3つの角がすべて等しい \(\triangle {\rm ABC}\) は正三角形であることを証明せよ。
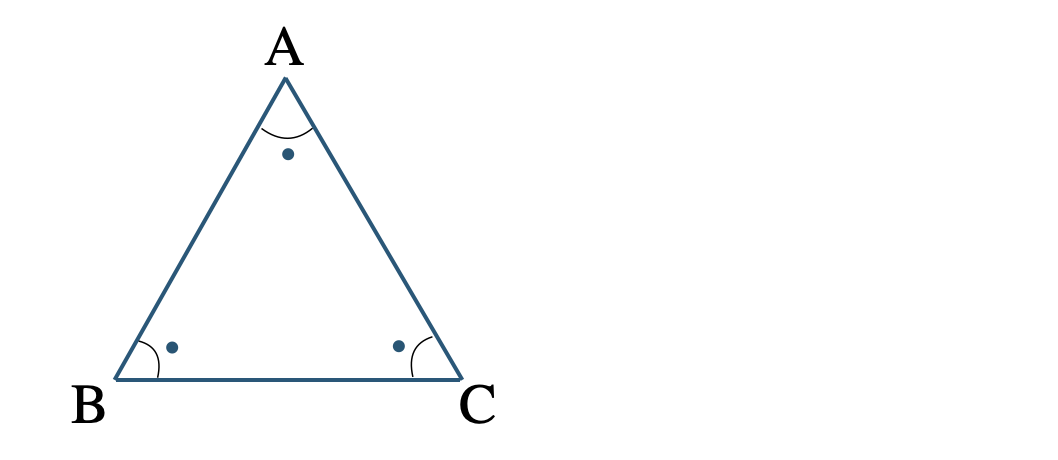
正三角形であることを示すために、3つの辺が等しければよい。(定義)
底角が等しい二等辺三角形の定理を使う。
底角が等しい二等辺三角形の定理を使う。
[証明] \(\triangle {\rm ABC}\) において、
\(\angle{\rm B}=\angle{\rm C}\) より、底角が等しいので、\(\angle{\rm A}\) を頂角とする二等辺三角形となる
よって、二等辺三角形の定義より、
\(~~~{\rm AB=AC}~~~\cdots{\large ①}\)
また、\(\angle{\rm A}=\angle{\rm C}\) より、底角が等しいので、\(\angle{\rm B}\) を頂角とする二等辺三角形となる
よって、二等辺三角形の定義より、
\(~~~{\rm BA=BC}~~~\cdots{\large ②}\)
①、②より、
\(~~~{\rm AB=BC=CA}\)
したがって、3つの辺が等しいので、
\(\triangle {\rm ABC}\) は正三角形
である [終]

【問題一覧】中2|三角形と四角形
このページは「中学数学2 三角形と四角形」の問題一覧ページとなります。解説の見たい単元名がわからない...


