問題:平行線と面積
次の問いに答えよ。
\({\small (1)}~\)▱ \({\rm ABCD}\) で辺 \({\rm BC~,~CD}\) の中点をそれぞれ \({\rm E~,~F}\) として \({\rm BD\,//\,EF}\) であるとき、\(\triangle {\rm ABE}\) と同じ面積の三角形をすべて答えよ。
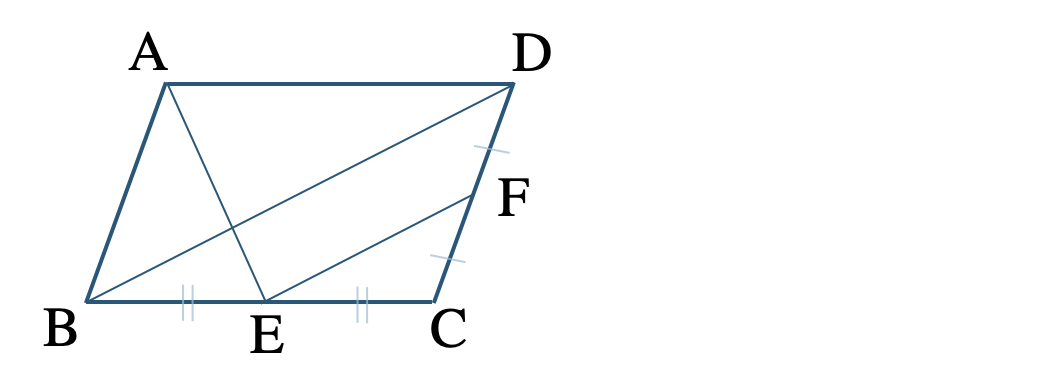
\({\small (2)}~\)四角形 \({\rm ABCD}\) で \({\rm AD\,//\,BC}\) であり、対角線 \({\rm AC~,~BD}\) の交点を \({\rm O}\) とするとき、\(\triangle {\rm ABO}=\triangle {\rm DCO}\) であることを証明せよ。

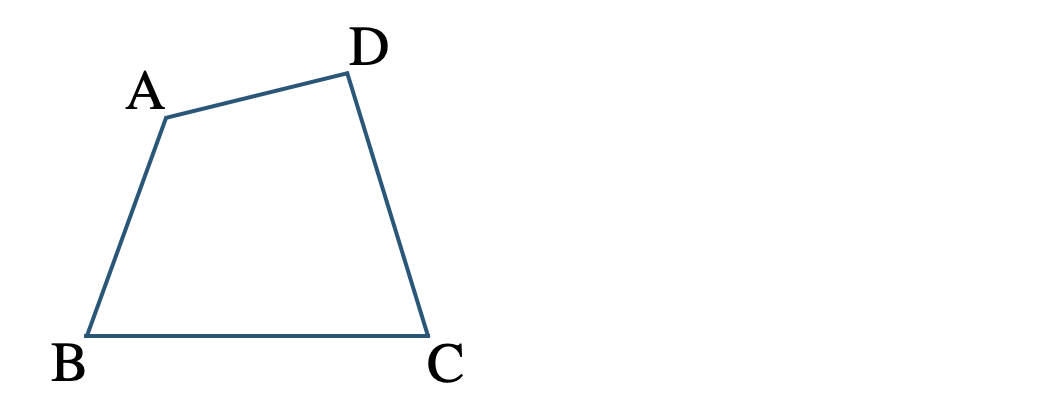
\({\small (3)}~\)図の四角形 \({\rm ABCD}\) の面積を変えずに三角形にするにはどのようにすればよいか答えよ。
\({\small (4)}~\)長方形 \({\rm ABCD}\) が境界線で2つの部分①、②に分けられる。
①と②の面積を変えずに、点 \({\rm E}\) を通る直線で境界線をひきなおすとき、どのようにひけばよいか答えよ。

解法のPoint
■ 平行線と面積
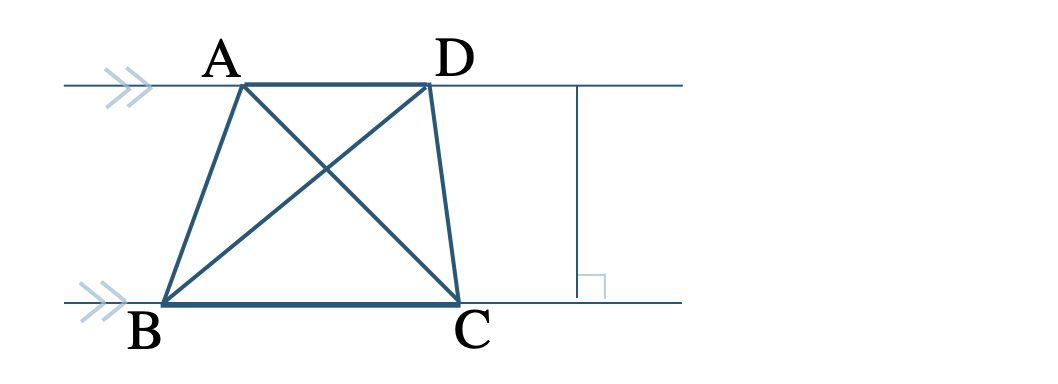
\({\rm AD\,//\,BC}\) のとき、辺 \({\rm BC}\) を底辺とする2つの三角形 \(\triangle {\rm ABC}\) と \(\triangle {\rm DBC}\) は高さが等しくなるので、面積が等しい。
よって、
\({\rm AD\,//\,BC}\) ならば \(\triangle {\rm ABC}=\triangle {\rm DBC}\)
また、これの逆も成り立つ。
\(\triangle {\rm ABC}=\triangle {\rm DBC}\) ならば \({\rm AD\,//\,BC}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:平行線と面積
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)▱ \({\rm ABCD}\) で辺 \({\rm BC~,~CD}\) の中点をそれぞれ \({\rm E~,~F}\) として \({\rm BD\,//\,EF}\) であるとき、\(\triangle {\rm ABE}\) と同じ面積の三角形をすべて答えよ。

\({\rm AD\,//\,BC}\) より、辺 \({\rm BE}\) を底辺とする三角形について、
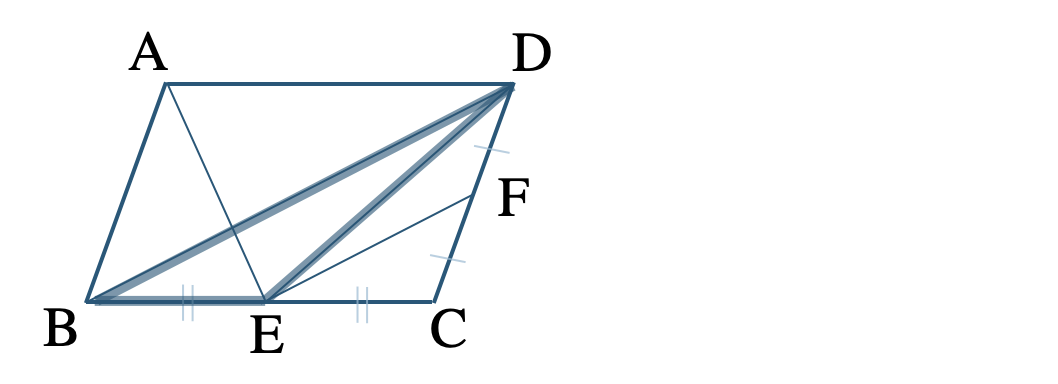
\(\triangle {\rm ABE}=\triangle {\rm DBE}\)
次に、\({\rm BE=EC}\) より、\({\rm EC}\) を底辺とする三角形について、
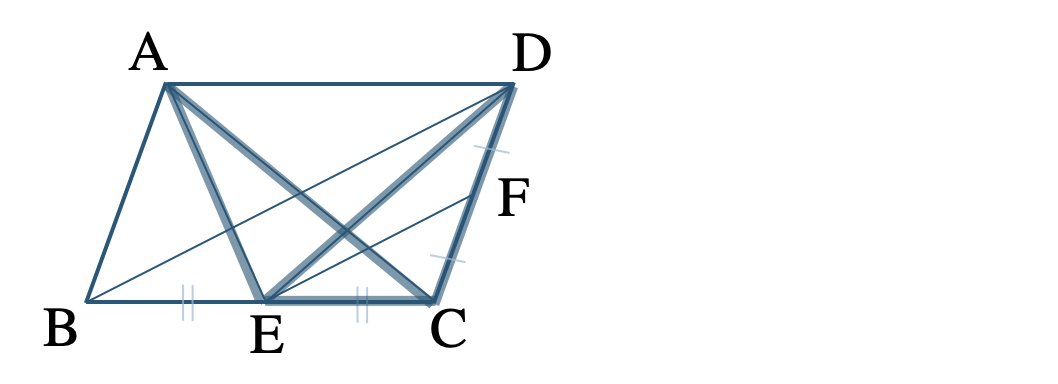
\(\triangle {\rm ABE}=\triangle {\rm DEC}=\triangle {\rm AEC}\)
次に、\({\rm BD\,//\,EF}\) より、\({\rm BD}\) を底辺とする三角形について、
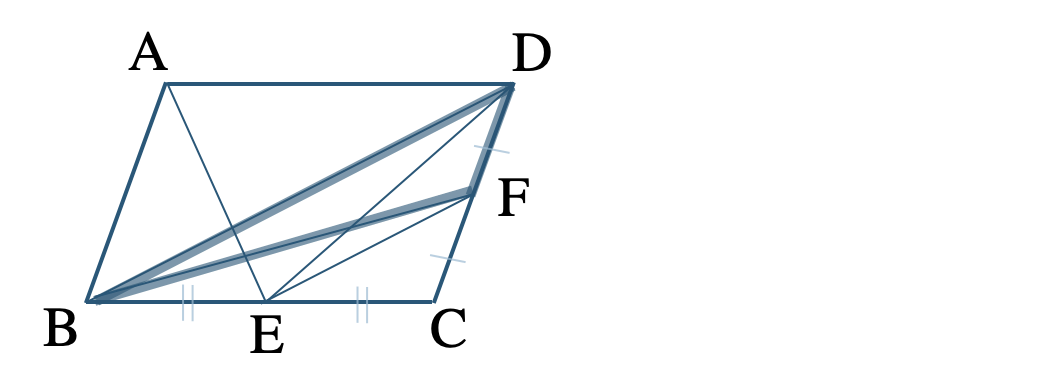
\(\triangle {\rm DBE}=\triangle {\rm DBF}\)
次に、\({\rm AB\,//\,DC}\) より、\({\rm DF}\) を底辺とする三角形について、
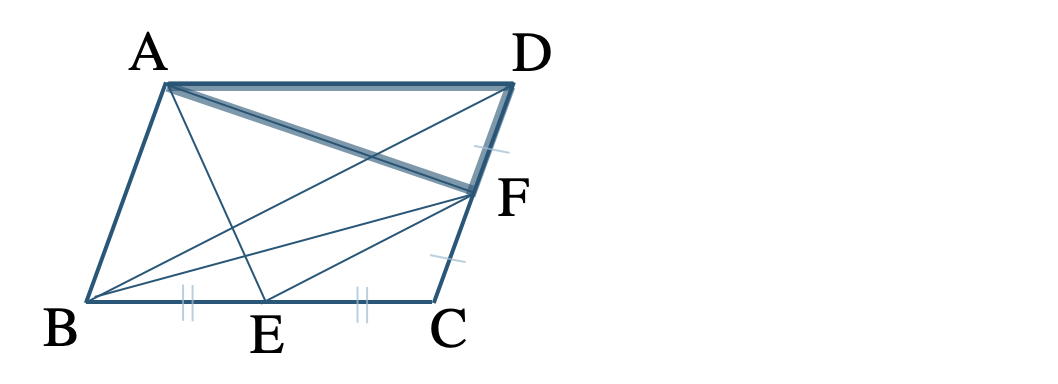
\(\triangle {\rm DBF}=\triangle {\rm AFD}\)
次に、\({\rm CF=FD}\) より、\({\rm CF}\) を底辺とする三角形について、
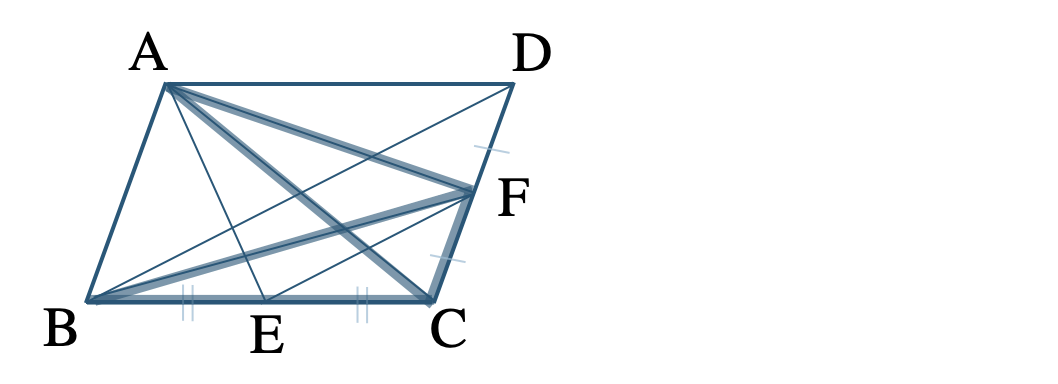
\(\triangle {\rm AFD}=\triangle {\rm ACF}=\triangle {\rm BCF}\)
したがって、\(\triangle {\rm ABE}\) と同じ面積の三角形は、
\(\triangle {\rm DBE}~,~\triangle {\rm DEC}~,~\triangle {\rm AEC}~,~\triangle {\rm DBF}~,~\)
\(\triangle {\rm AFD}~,~\triangle {\rm ACF}~,~\triangle {\rm BCF}\)
となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)四角形 \({\rm ABCD}\) で \({\rm AD\,//\,BC}\) であり、対角線 \({\rm AC~,~BD}\) の交点を \({\rm O}\) とするとき、\(\triangle {\rm ABO}=\triangle {\rm DCO}\) であることを証明せよ。

・\(\triangle {\rm ABO}=\triangle {\rm DCO}\) を示すために、\({\rm AD\,//\,BC}\) より、\(\triangle {\rm ABC}=\triangle {\rm DBC}\) となることを使う。

[証明] \({\rm AD\,//\,BC}\) より、\({\rm BC}\) を底辺とする三角形について、
\(\triangle {\rm ABC}=\triangle {\rm DBC}\)
ここで、
\(\triangle {\rm ABC}=\triangle {\rm ABO}+\triangle {\rm OBC}\)
\(\triangle {\rm DBC}=\triangle {\rm DOC}+\triangle {\rm OBC}\)
\(\triangle {\rm OBC}\) が共通しているので、
\(\triangle {\rm ABO}=\triangle {\rm DOC}\)
[終]
問題解説(3)
次の問いに答えよ。
\({\small (3)}~\)図の四角形 \({\rm ABCD}\) の面積を変えずに三角形にするにはどのようにすればよいか答えよ。

対角線 \({\rm AC}\) をひき、これに平行で点 \({\rm D}\) を通る直線をひく
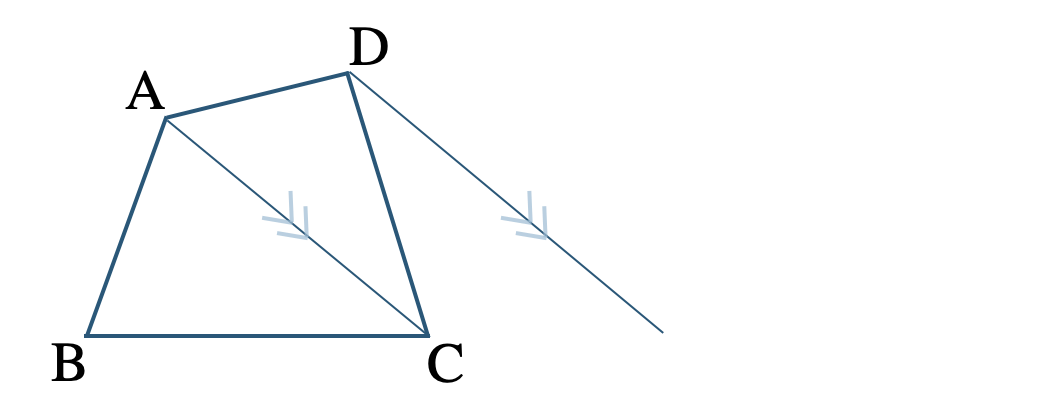
この平行線と辺 \({\rm BC}\) の延長線との交点を \({\rm E}\) とする
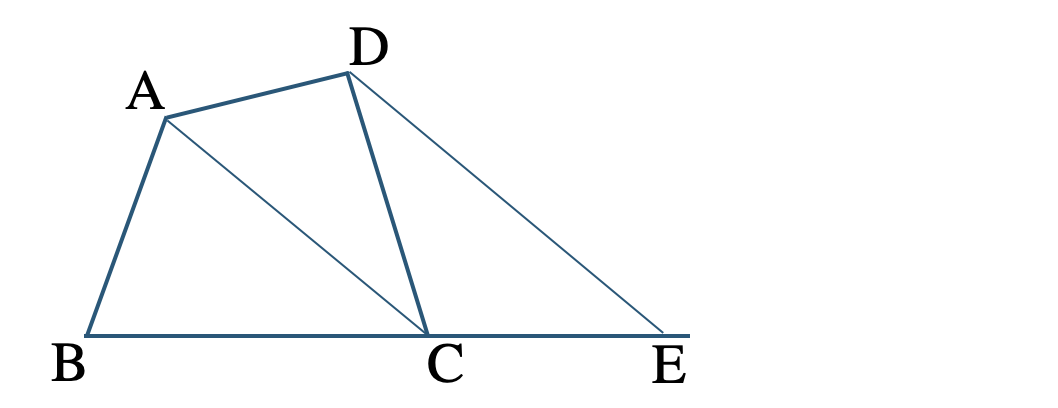
線分 \({\rm AE}\) をひくと、\({\rm AC\,//\,DE}\) より、
\(\triangle {\rm ACD}=\triangle {\rm ACE}\)
となるので、
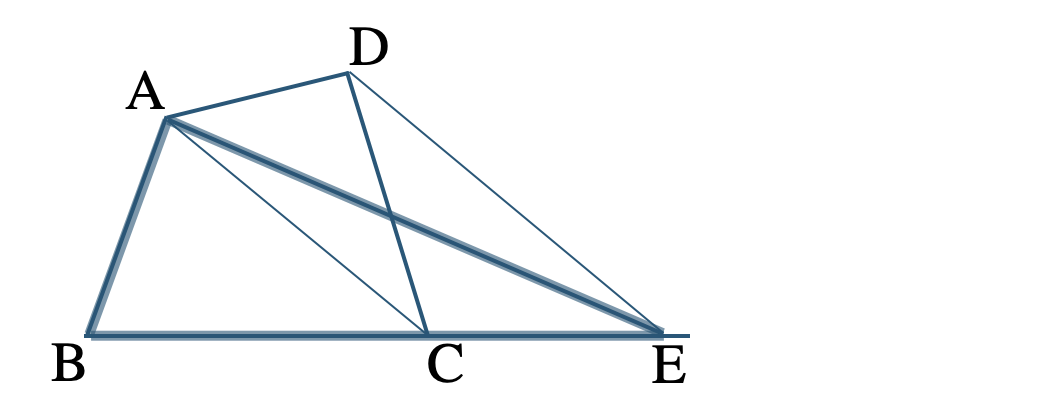
\(\triangle {\rm ABE}\) がもとの四角形 \({\rm ABCD}\) と面積が等しくなる
問題解説(4)
次の問いに答えよ。
\({\small (4)}~\)長方形 \({\rm ABCD}\) が境界線で2つの部分①、②に分けられる。
①と②の面積を変えずに、点 \({\rm E}\) を通る直線で境界線をひきなおすとき、どのようにひけばよいか答えよ。

線分 \({\rm EF}\) をひき、これに平行で点 \({\rm G}\) を通る直線をひく
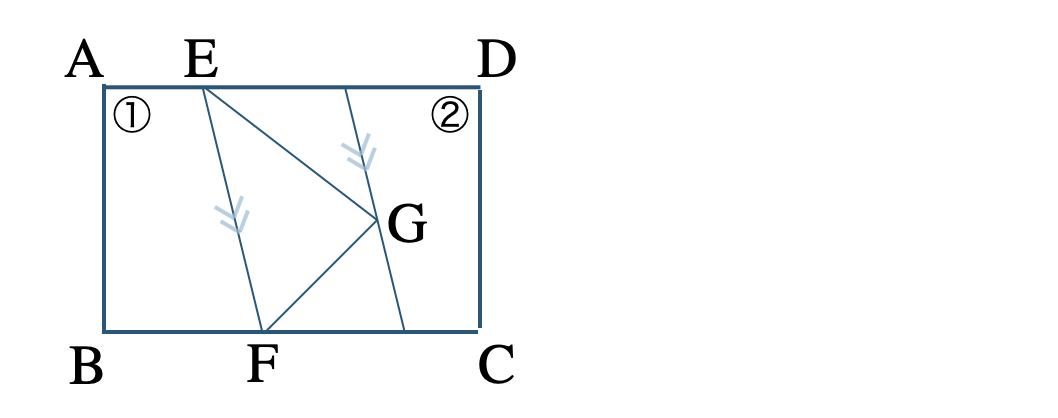
この平行線と辺 \({\rm BC}\) との交点を \({\rm H}\) とする
\({\rm EH}\) をひくと \({\rm EF\,//\,GH}\) より、
\(\triangle {\rm EFG}=\triangle {\rm EFH}\)
となる
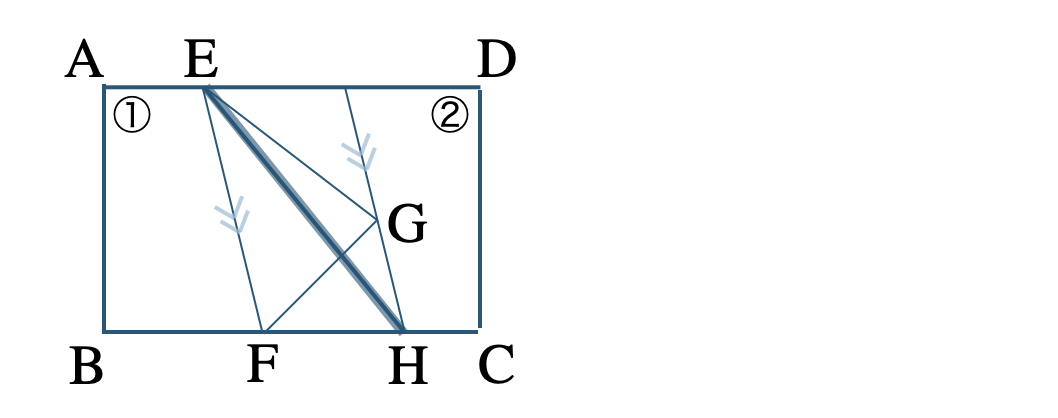
したがって、
線分 \({\rm EH}\) によって、①と②の面積を変えずに境界線をひきなおせる



