今回の問題は「三平方の定理の逆」です。
\(~\)数研出版 これからの数学３ p.197~198 問1~3
\(~\)東京書籍 新しい数学３ p.191 問1
\(~\)啓林館 未来へひろがる数学３ p.186 問4
問題
\({\small (1)}~3~{\rm cm}~,~6~{\rm cm}~,~8~{\rm cm}\)
\({\small (2)}~6~{\rm cm}~,~8~{\rm cm}~,~10~{\rm cm}\)
\({\small (3)}~5~{\rm cm}~,~5~{\rm cm}~,~5\sqrt{2}~{\rm cm}\)
\({\small (4)}~\sqrt{13}~{\rm cm}~,~\sqrt{17}~{\rm cm}~,~\sqrt{39}~{\rm cm}\)
\({\small (5)}~\sqrt{2}~{\rm cm}~,~\sqrt{6}~{\rm cm}~,~2\sqrt{2}~{\rm cm}\)
三角形の３辺の長さが次のとき、この三角形が直角三角形であるか調べよ。
\({\small (1)}~3~{\rm cm}~,~6~{\rm cm}~,~8~{\rm cm}\)
\({\small (2)}~6~{\rm cm}~,~8~{\rm cm}~,~10~{\rm cm}\)
\({\small (3)}~5~{\rm cm}~,~5~{\rm cm}~,~5\sqrt{2}~{\rm cm}\)
\({\small (4)}~\sqrt{13}~{\rm cm}~,~\sqrt{17}~{\rm cm}~,~\sqrt{39}~{\rm cm}\)
\({\small (5)}~\sqrt{2}~{\rm cm}~,~\sqrt{6}~{\rm cm}~,~2\sqrt{2}~{\rm cm}\)
Point：三平方の定理の逆
\(a^2+b^2=c^2\) が成り立つとき、
この \(\triangle {\rm ABC}\) は長さ \(c\) の辺を斜辺とする直角三角形である
※ \(\angle{\rm C}=90^\circ\) の直角三角形
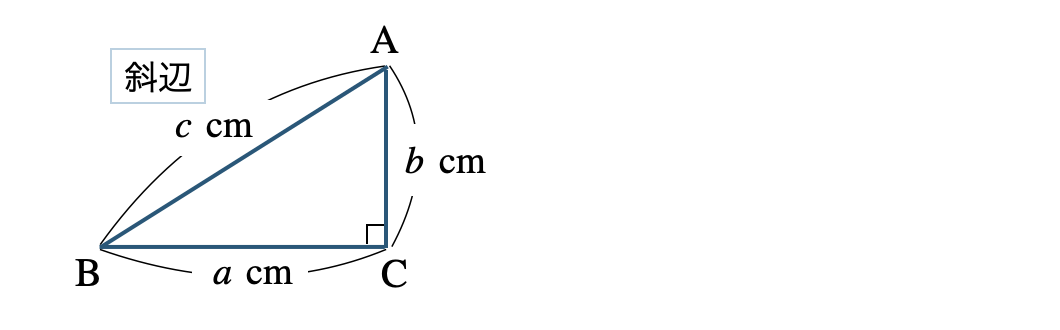
\(\triangle {\rm ABC}\) の３辺の長さ \(a~,~b~,~c\) について、
\(a^2+b^2=c^2\) が成り立つとき、
この \(\triangle {\rm ABC}\) は長さ \(c\) の辺を斜辺とする直角三角形である
※ \(\angle{\rm C}=90^\circ\) の直角三角形
たとえば、\(a=3~{\rm cm}~,~b=4~{\rm cm}~,~c=5~{\rm cm}\) のとき、
もっとも長い辺が \(c=5~{\rm cm}\) より、
\(a^2+b^2=3^2+4^2=25\)
\(c^2=25\)
これより、\(a^2+b^2=c^2\) が成り立つので \(\triangle {\rm ABC}\) は直角三角形となる
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
次のページ「解法のPointと問題解説」
