正の数・負の数の減法の解法
正の数・負の数の減法は、
引き算する数の符号をかえて、足し算にする
ことで正の数・負の数の加法として計算できる。
たとえば、\((+2)-(-3)\) は、
反対の性質をもつことばより、
負の数 \(-3\) \(\leftrightarrow\) 正の数 \(+3\)
引き算 \(\leftrightarrow\) 足し算
負の数 \(-3\) を引き算することは、正の数 \(+3\) を足し算することである。
これより、
\(\begin{split}&(+2)-(-3)\\[2pt]~~=~&(+2)+(+3)\\[2pt]~~=~&+(2+3)\\[2pt]~~=~&+5\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説：正の数・負の数の減法
問題解説(1)
次の計算をせよ。
\({\small (1)}~~(+3)-(+5)\)
正の数 \(+5\) を引き算することは、
負の数 \(-5\) を足し算することであるので、
\(\begin{split}&(+3)-(+5)\\[2pt]~~=~&(+3)+(-5)\end{split}\)
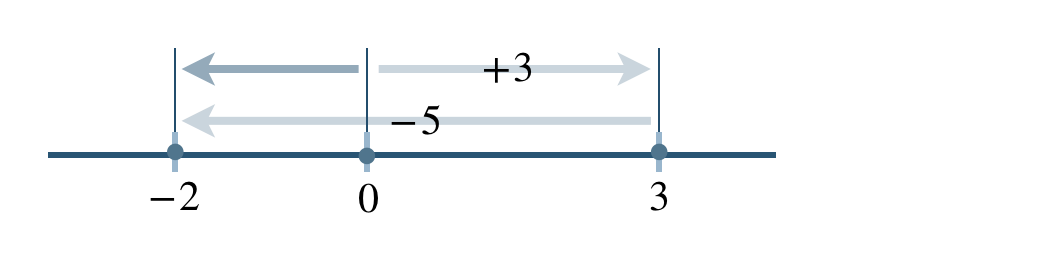
\(\begin{split}~~=~&-(5-3)\\[2pt]~~=~&-2\end{split}\)
したがって、答えは \(-2\) となる
問題解説(2)
次の計算をせよ。
\({\small (2)}~~(+5)-(-2)\)
負の数 \(-2\) を引き算することは、
正の数 \(+2\) を足し算することであるので、
\(\begin{split}&(+5)-(-2)\\[2pt]~~=~&(+5)+(+2)\end{split}\)
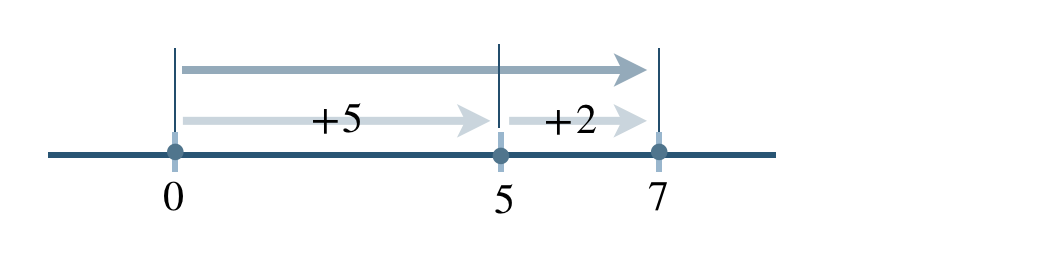
\(\begin{split}~~=~&+(5+2)\\[2pt]~~=~&7\end{split}\)
したがって、答えは \(7\) となる
問題解説(3)
次の計算をせよ。
\({\small (3)}~~(-2)-(+4)\)
正の数 \(+4\) を引き算することは、
負の数 \(-4\) を足し算することであるので、
\(\begin{split}&(-2)-(+4)\\[2pt]~~=~&(-2)+(-4)\end{split}\)
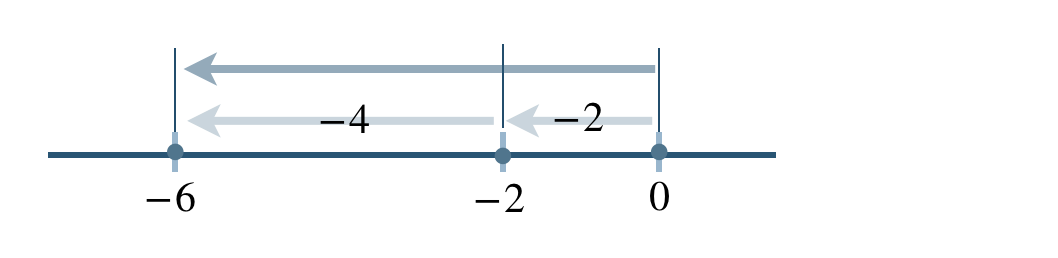
\(\begin{split}~~=~&-(2+4)\\[2pt]~~=~&-6\end{split}\)
したがって、答えは \(-6\) となる
問題解説(4)
次の計算をせよ。
\({\small (4)}~~(-3)-(-7)\)
負の数 \(-7\) を引き算することは、
正の数 \(+7\) を足し算することであるので、
\(\begin{split}&(-3)-(-7)\\[2pt]~~=~&(-3)+(+7)\end{split}\)
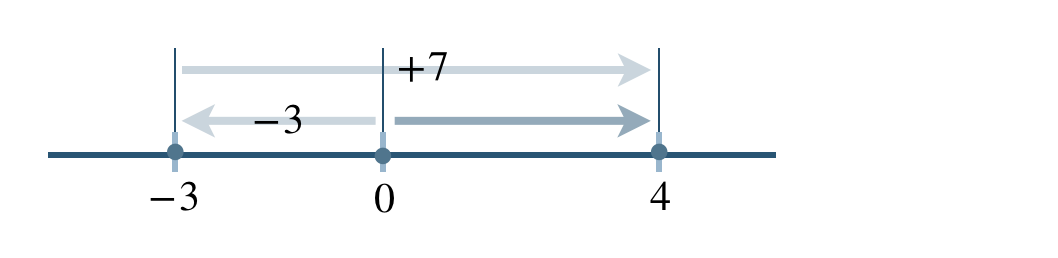
\(\begin{split}~~=~&+(7-3)\\[2pt]~~=~&4\end{split}\)
したがって、答えは \(4\) となる
問題解説(5)
次の計算をせよ。
\({\small (5)}~~(-8)-(-1)\)
負の数 \(-1\) を引き算することは、
正の数 \(+1\) を足し算することであるので、
\(\begin{split}&(-8)-(-1)\\[2pt]~~=~&(-8)+(+1)\end{split}\)
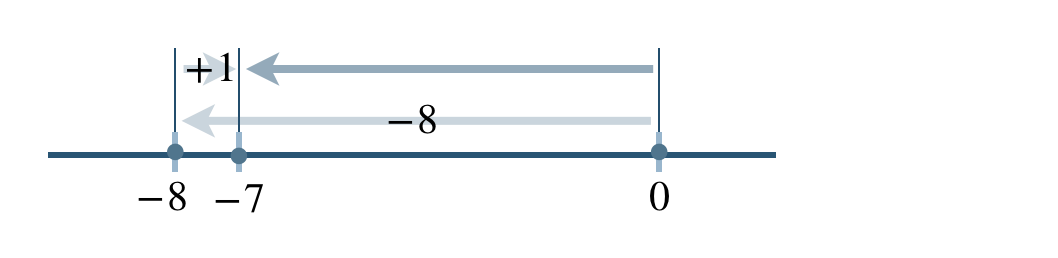
\(\begin{split}~~=~&-(8-1)\\[2pt]~~=~&-7\end{split}\)
したがって、答えは \(-7\) となる
問題解説(6)
次の計算をせよ。
\({\small (6)}~~(-5)-0\)
\(0\) は引いても結果がかわらないので、
\(\begin{split}&(-5)-0\\[2pt]~~=~&-5\end{split}\)
したがって、答えは \(-5\) となる
問題解説(7)
次の計算をせよ。
\({\small (7)}~~0-(+12)\)
正の数 \(+12\) を引き算することは、
負の数 \(-12\) を足し算することであるので、
\(\begin{split}&0-(+12)\\[2pt]~~=~&0+(-12)\\[2pt]~~=~&-12\end{split}\)
したがって、答えは \(-12\) となる
問題解説(8)
次の計算をせよ。
\({\small (8)}~~0-(-14)\)
負の数 \(-14\) を引き算することは、
正の数 \(+14\) を足し算することであるので、
\(\begin{split}&0-(-14)\\[2pt]~~=~&0+(+14)\\[2pt]~~=~&+14\end{split}\)
したがって、答えは \(+14\) となる
