分数や小数の加法・減法の解法
Point：小数の加法・減法
\((-0.3)-(-1.5)\)
① 減法を加法にする。(反対の性質のことば)
負の数 \(-1.5\) を引き算することは、
正の数 \(+1.5\) を足し算することであるので、
\(\begin{split}~~=~&(-0.3)+(+1.5)\end{split}\)
② 絶対値を調べて、符号と数を決める。
絶対値は \(1.5 > 0.3\) であるので、
符号はプラスで、数は \(1.5-0.3\)
\(\begin{split}~~=~&+(1.5-0.3)\\[2pt]~~=~&1.2\end{split}\)
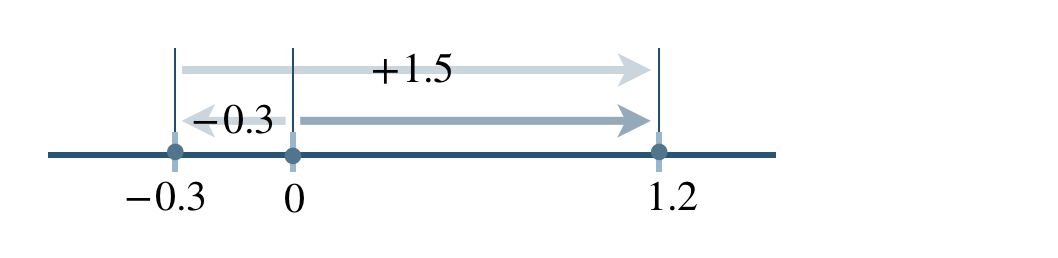
小数のときも整数と同じように計算する。
\((-0.3)-(-1.5)\)
① 減法を加法にする。(反対の性質のことば)
負の数 \(-1.5\) を引き算することは、
正の数 \(+1.5\) を足し算することであるので、
\(\begin{split}~~=~&(-0.3)+(+1.5)\end{split}\)
② 絶対値を調べて、符号と数を決める。
絶対値は \(1.5 > 0.3\) であるので、
符号はプラスで、数は \(1.5-0.3\)
\(\begin{split}~~=~&+(1.5-0.3)\\[2pt]~~=~&1.2\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point：分数の加法・減法
\(\begin{split} \left(+\frac{\,1\,}{\,5\,}\right)-\left(+\frac{\,1\,}{\,2\,}\right) \end{split}\)
① 減法を加法にする。(反対の性質のことば)
\(\begin{split}&~~=~&\left(+\frac{\,1\,}{\,5\,}\right)+\left(-\frac{\,1\,}{\,2\,}\right)\end{split}\)
② 通分する。(大小を比べやすくなる)
\(\begin{split}~~=~&\left(+\frac{\,1{\, \small \times \,}2\,}{\,5{\, \small \times \,}2\,}\right)+\left(-\frac{\,1{\, \small \times \,}5\,}{\,2{\, \small \times \,}5\,}\right)\\[3pt]~~=~&\left(+\frac{\,2\,}{\,10\,}\right)+\left(-\frac{\,5\,}{\,10\,}\right)\end{split}\)
③ 絶対値を調べて、符号と数を決める。
絶対値は \(\begin{split}\frac{\,5\,}{\,10\,} > \frac{\,2\,}{\,10\,}\end{split}\) であるので、
符号はマイナスで、数は \(\begin{split}\frac{\,5\,}{\,10\,}-\frac{\,2\,}{\,10\,}\end{split}\)
\(\begin{split}~~=~&-\left(\frac{\,5\,}{\,10\,}-\frac{\,2\,}{\,10\,}\right)\\[3pt]~~=~&-\frac{\,3\,}{\,10\,}\end{split}\)
分数の加法や減法は、
\(\begin{split} \left(+\frac{\,1\,}{\,5\,}\right)-\left(+\frac{\,1\,}{\,2\,}\right) \end{split}\)
① 減法を加法にする。(反対の性質のことば)
\(\begin{split}&~~=~&\left(+\frac{\,1\,}{\,5\,}\right)+\left(-\frac{\,1\,}{\,2\,}\right)\end{split}\)
② 通分する。(大小を比べやすくなる)
\(\begin{split}~~=~&\left(+\frac{\,1{\, \small \times \,}2\,}{\,5{\, \small \times \,}2\,}\right)+\left(-\frac{\,1{\, \small \times \,}5\,}{\,2{\, \small \times \,}5\,}\right)\\[3pt]~~=~&\left(+\frac{\,2\,}{\,10\,}\right)+\left(-\frac{\,5\,}{\,10\,}\right)\end{split}\)
③ 絶対値を調べて、符号と数を決める。
絶対値は \(\begin{split}\frac{\,5\,}{\,10\,} > \frac{\,2\,}{\,10\,}\end{split}\) であるので、
符号はマイナスで、数は \(\begin{split}\frac{\,5\,}{\,10\,}-\frac{\,2\,}{\,10\,}\end{split}\)
\(\begin{split}~~=~&-\left(\frac{\,5\,}{\,10\,}-\frac{\,2\,}{\,10\,}\right)\\[3pt]~~=~&-\frac{\,3\,}{\,10\,}\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説：分数や小数の加法・減法
問題解説(1)
問題
\({\small (1)}~~(-1.3)+(-1.7)\)
次の計算をせよ。
\({\small (1)}~~(-1.3)+(-1.7)\)
数直線上に表すと、
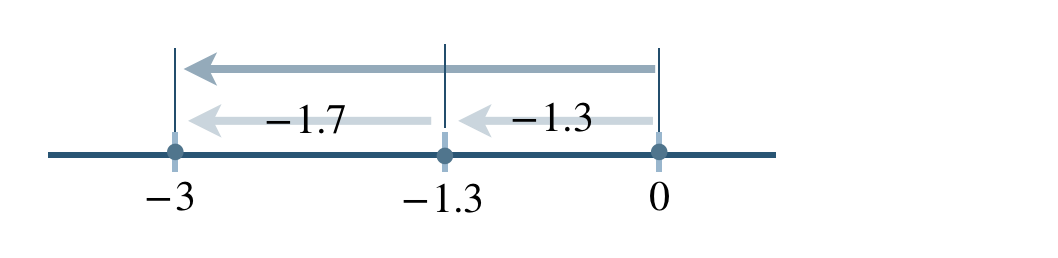
\(\begin{split}&(-1.3)+(-1.7)\\[2pt]~~=~&-(1.3+1.7)\\[2pt]~~=~&-3\end{split}\)
したがって、答えは \(-3\) となる
問題解説(2)
問題
\({\small (2)}~~(+0.2)-(-2.2)\)
次の計算をせよ。
\({\small (2)}~~(+0.2)-(-2.2)\)
負の数 \(-2.2\) を引き算することは、
正の数 \(+2.2\) を足し算することであるので、
\(\begin{split}&(+0.2)-(-2.2)\\[2pt]~~=~&(+0.2)+(+2.2)\end{split}\)
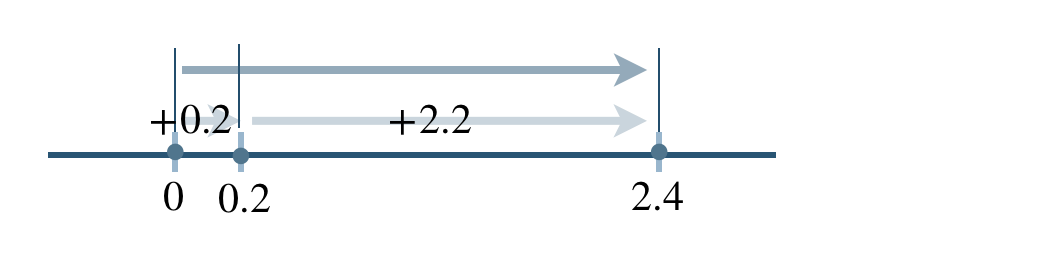
\(\begin{split}~~=~&+(0.2+2.2)\\[2pt]~~=~&2.4\end{split}\)
したがって、答えは \(+2.4\) となる
問題解説(3)
問題
\({\small (3)}~~(-3.5)-(-1.5)\)
次の計算をせよ。
\({\small (3)}~~(-3.5)-(-1.5)\)
負の数 \(-1.5\) を引き算することは、
正の数 \(+1.5\) を足し算することであるので、
\(\begin{split}&(-3.5)-(-1.5)\\[2pt]~~=~&(-3.5)+(+1.5)\end{split}\)
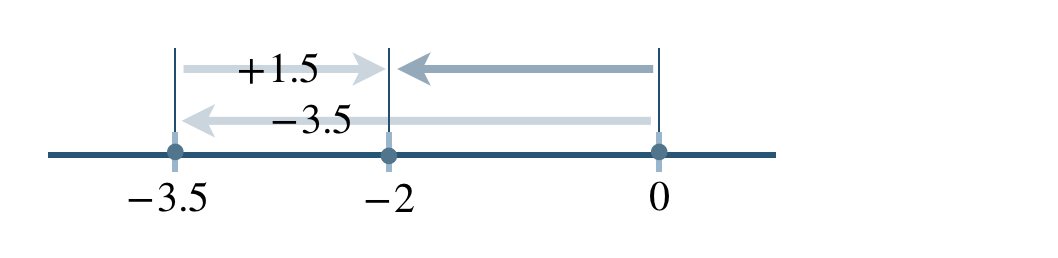
\(\begin{split}~~=~&-(3.5-1.5)\\[2pt]~~=~&-2\end{split}\)
したがって、答えは \(-2\) となる
問題解説(4)
問題
\({\small (4)}\)\(\begin{split}~~\left(+\frac{\,1\,}{\,3\,}\right)+\left(-\frac{\,2\,}{\,3\,}\right)\end{split}\)
次の計算をせよ。
\({\small (4)}\)\(\begin{split}~~\left(+\frac{\,1\,}{\,3\,}\right)+\left(-\frac{\,2\,}{\,3\,}\right)\end{split}\)
それぞれの絶対値を比べると、
絶対値は \(\begin{split}\frac{\,2\,}{\,3\,} > \frac{\,1\,}{\,3\,}\end{split}\) であるので、
符号はマイナスで、数は \(\begin{split}\frac{\,2\,}{\,3\,}-\frac{\,1\,}{\,3\,}\end{split}\)
\(\begin{split}&\left(+\frac{\,1\,}{\,3\,}\right)+\left(-\frac{\,2\,}{\,3\,}\right)\\[3pt]~~=~&-\left(\frac{\,2\,}{\,3\,}-\frac{\,1\,}{\,3\,}\right)\\[3pt]~~=~&-\left(\frac{\,2-1\,}{\,3\,}\right)\\[3pt]~~=~&-\frac{\,1\,}{\,3\,}\end{split}\)
したがって、答えは \(\begin{split}-\frac{\,1\,}{\,3\,}\end{split}\) となる
問題解説(5)
問題
\({\small (5)}\)\(\begin{split}~~\left(-\frac{\,1\,}{\,2\,}\right)-\left(-\frac{\,1\,}{\,3\,}\right)\end{split}\)
次の計算をせよ。
\({\small (5)}\)\(\begin{split}~~\left(-\frac{\,1\,}{\,2\,}\right)-\left(-\frac{\,1\,}{\,3\,}\right)\end{split}\)
負の数 \(\begin{split}- \frac{\,1\,}{\,3\,}\end{split}\) を引き算することは、
正の数 \(\begin{split}+\frac{\,1\,}{\,3\,}\end{split}\) を足し算することであるので、
\(\begin{split}&\left(-\frac{\,1\,}{\,2\,}\right)-\left(-\frac{\,1\,}{\,3\,}\right)
\\[3pt]~~=~&\left(-\frac{\,1\,}{\,2\,}\right)+\left(+\frac{\,1\,}{\,3\,}\right)\end{split}\)
通分すると、
\(\begin{split}~~=~&\left(-\frac{\,1{\, \small \times \,}3\,}{\,2{\, \small \times \,}3\,}\right)+\left(+\frac{\,1{\, \small \times \,}2\,}{\,3{\, \small \times \,}2\,}\right)
\\[3pt]~~=~&\left(-\frac{\,3\,}{\,6\,}\right)+\left(+\frac{\,2\,}{\,6\,}\right)\end{split}\)
それぞれの絶対値を比べると、
絶対値は \(\begin{split}\frac{\,3\,}{\,6\,} > \frac{\,2\,}{\,6\,}\end{split}\) であるので、
符号はマイナスで、数は \(\begin{split}\frac{\,3\,}{\,6\,}-\frac{\,2\,}{\,6\,}\end{split}\)
\(\begin{split}~~=~&-\left(\frac{\,3\,}{\,6\,}-\frac{\,2\,}{\,6\,}\right)\\[3pt]~~=~&-\left(\frac{\,3-2\,}{\,6\,}\right)\\[3pt]~~=~&-\frac{\,1\,}{\,6\,}\end{split}\)
したがって、答えは \(\begin{split}-\frac{\,1\,}{\,6\,}\end{split}\) となる
問題解説(6)
問題
\({\small (6)}\)\(\begin{split}~~\left(+\frac{\,3\,}{\,7\,}\right)-\left(-\frac{\,1\,}{\,3\,}\right)\end{split}\)
次の計算をせよ。
\({\small (6)}\)\(\begin{split}~~\left(+\frac{\,3\,}{\,7\,}\right)-\left(-\frac{\,1\,}{\,3\,}\right)\end{split}\)
負の数 \(\begin{split}-\frac{\,1\,}{\,3\,}\end{split}\) を引き算することは、
正の数 \(\begin{split}+\frac{\,1\,}{\,3\,}\end{split}\) を足し算することであるので、
\(\begin{split}&\left(+\frac{\,3\,}{\,7\,}\right)-\left(-\frac{\,1\,}{\,3\,}\right)
\\[3pt]~~=~&\left(+\frac{\,3\,}{\,7\,}\right)+\left(+\frac{\,1\,}{\,3\,}\right)\end{split}\)
通分すると、
\(\begin{split}&\left(+\frac{\,3{\, \small \times \,}3\,}{\,7{\, \small \times \,}3\,}\right)+\left(+\frac{\,1{\, \small \times \,}7\,}{\,3{\, \small \times \,}7\,}\right)
\\[3pt]~~=~&\left(+\frac{\,9\,}{\,21\,}\right)+\left(+\frac{\,7\,}{\,21\,}\right)\end{split}\)
同じ符号であるから、共通の符号で、絶対値の和より、
\(\begin{split}~~=~&+\left(\frac{\,9\,}{\,21\,}+\frac{\,7\,}{\,21\,}\right)\\[3pt]~~=~&+\left(\frac{\,9+7\,}{\,21\,}\right)\\[3pt]~~=~&\frac{\,16\,}{\,21\,}\end{split}\)
したがって、答えは \(\begin{split}\frac{\,16\,}{\,21\,}\end{split}\) となる
【問題一覧】中１｜正の数と負の数
このページは「中学数学１ 正の数と負の数」の問題一覧ページとなります。解説の見たい単元名がわからない...
jhs.yorikuwa.com
