数量を文字で表す

Point：数量を文字で表す

数のかわりに \(x\) や \(a\) などの文字を使って、数量を表すことができる。

---

たとえば、
\({\small (1)}~\)\(a\) 円のものを \(b\) 個買ったとき、
　　→ 代金の合計は \((\,a{\, \small \times \,}b\,)\) 円

---

\({\small (2)}~\)\(a~{\rm cm}\) のひもから \(b~{\rm cm}\) 切ったとき、
　　→ 残りのひもの長さは \((\,a-b\,)~{\rm cm}\)

---

\({\small (3)}~\)\(a\) 個のものを \(b\) 人で分けるとき、
　　→ １人分は \((\,a{\, \small \div \,}b\,)\) 個

---

\({\small (4)}~\)\(a\) 円のものを \(b\) 円で支払ったとき、
　　→ 受け取るおつりは \((\,b-a\,)\) 円

---

\({\small (5)}~\)たて \(a~{\rm cm}\)、よこ \(b~{\rm cm}\) の長方形において、
　　→ 長方形の面積は \((\,a{\, \small \times \,}b\,)~{\rm cm^2}\)

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次の数量を、記号 \(+~,~-~,~{\, \small \times \,}~,~{\, \small \div \,}\) を使った文字式で表せ。

---

\({\small (1)}~\)１個 \(70\) 円のみかんを \(x\) 個買ったときの代金は何円。

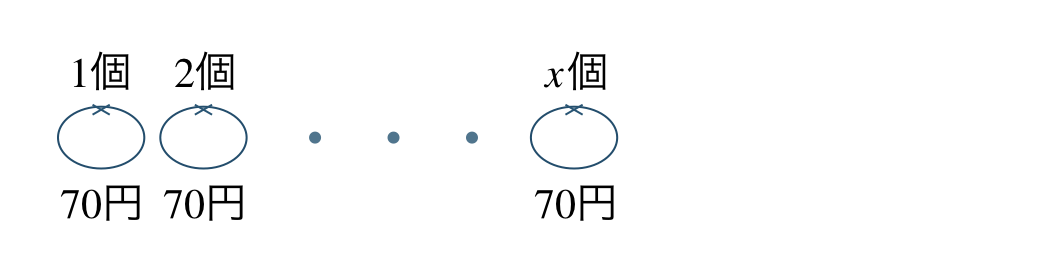
合計代金＝１個の値段 \({\, \small \times \,}\) 個数より、

---

答えは、\((\,70{\, \small \times \,} x\,)~\)円

問題

次の数量を、記号 \(+~,~-~,~{\, \small \times \,}~,~{\, \small \div \,}\) を使った文字式で表せ。

---

\({\small (2)}~\)\(100~{\rm cm}\) のひもから、\(a~{\rm cm}\) 切りとったときの残りの長さは何\(~{\rm cm}\)。

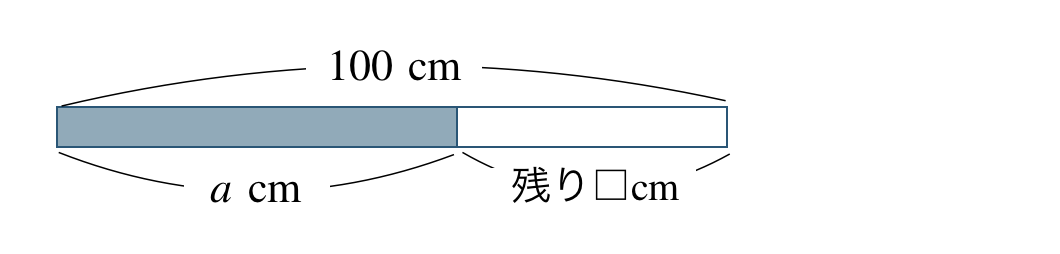
残りのひもの長さ＝もとの長さー切り取る長さより、

---

答えは、\((\,100-a\,)~{\rm cm}\)

問題

次の数量を、記号 \(+~,~-~,~{\, \small \times \,}~,~{\, \small \div \,}\) を使った文字式で表せ。

---

\({\small (3)}~\)\(x~{\rm L}\) のジュースを５人で等しく分けたときの１人分は何\(~{\rm L}\)。

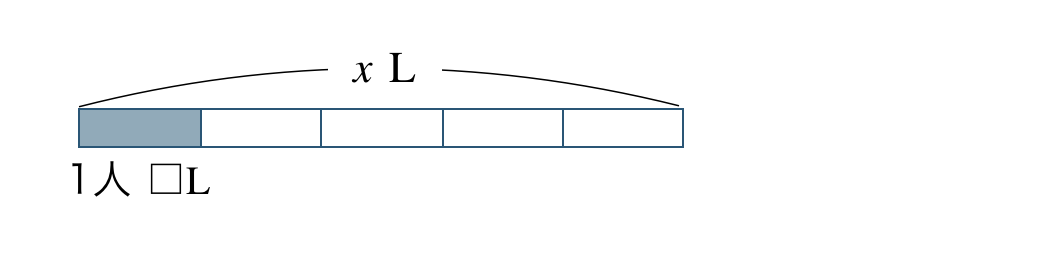
１人分＝全体 \({\, \small \div \,}\) 人数より、

---

答えは、\((\,x{\, \small \div \,} 5\,)~{\rm L}\)

問題

次の数量を、記号 \(+~,~-~,~{\, \small \times \,}~,~{\, \small \div \,}\) を使った文字式で表せ。

---

\({\small (4)}~\)１個 \(120\) 円のりんご \(a\) 個を \(1000\) 円で支払ったときのおつりは何円。

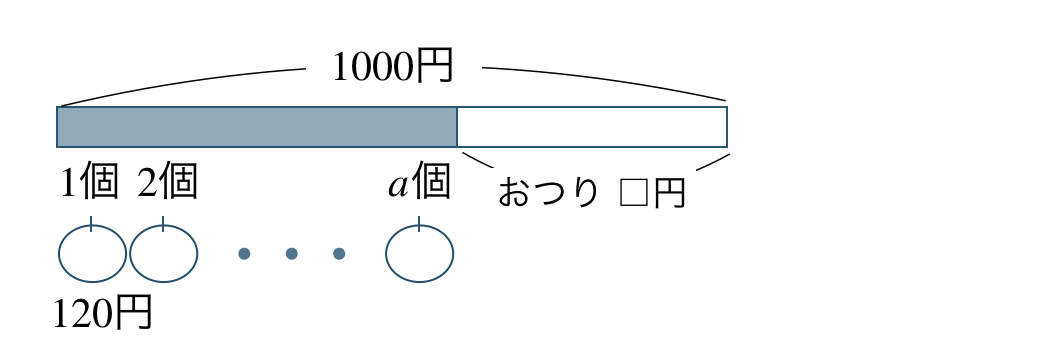
１個 \(120\) 円のりんご \(a\) 個の代金は、
　 \((\,120{\, \small \times \,} a\,)~\)個

---

おつり＝支払いー代金であるので、

---

\(1000\) 円で支払ったときのおつりは、
　 \((\,1000-120{\, \small \times \,} a\,)~\)円

問題

次の数量を、記号 \(+~,~-~,~{\, \small \times \,}~,~{\, \small \div \,}\) を使った文字式で表せ。

---

\({\small (5)}~\)つる \(x\) 匹、かめ \(y\) 匹の足の数の合計は何本。

つるだけの足の数の合計は、\((\,2{\, \small \times \,} x\,)~\)本
かめだけの足の数の合計は、\((\,4{\, \small \times \,} y\,)~\)本

---

よって、足の数合計は、
　 \((\,2{\, \small \times \,} x+4{\, \small \times \,} y)\,~\)本

問題

次の数量を、記号 \(+~,~-~,~{\, \small \times \,}~,~{\, \small \div \,}\) を使った文字式で表せ。

---

\({\small (6)}~\)底辺 \(a~{\rm cm}\)、高さ \(h~{\rm cm}\) の三角形の面積は何 \(~{\rm cm}^2\)。

三角形の面積の公式は、底辺\({\, \small \times \,}\)高さ\({\, \small \div \,}2\) であるので

答えは、\((\,a{\, \small \times \,} h {\, \small \div \,}2\,)~{\rm cm}^2\)