問題:グラフと比例・反比例の式
問題
\({\small (1)}~\)次の①と②の直線のグラフを \(y\) を \(x\) の式で表せ。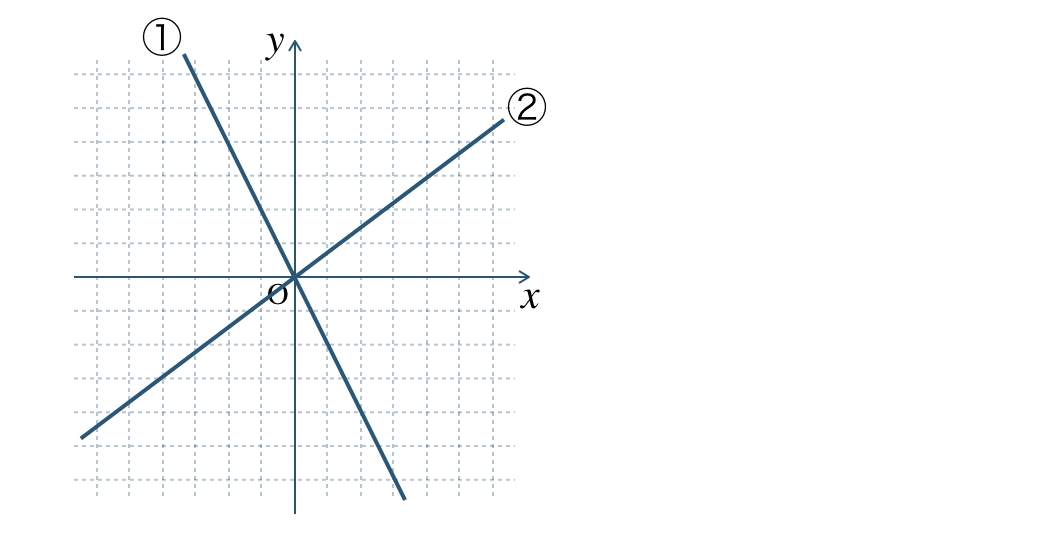
次の問いに答えよ。
\({\small (1)}~\)次の①と②の直線のグラフを \(y\) を \(x\) の式で表せ。

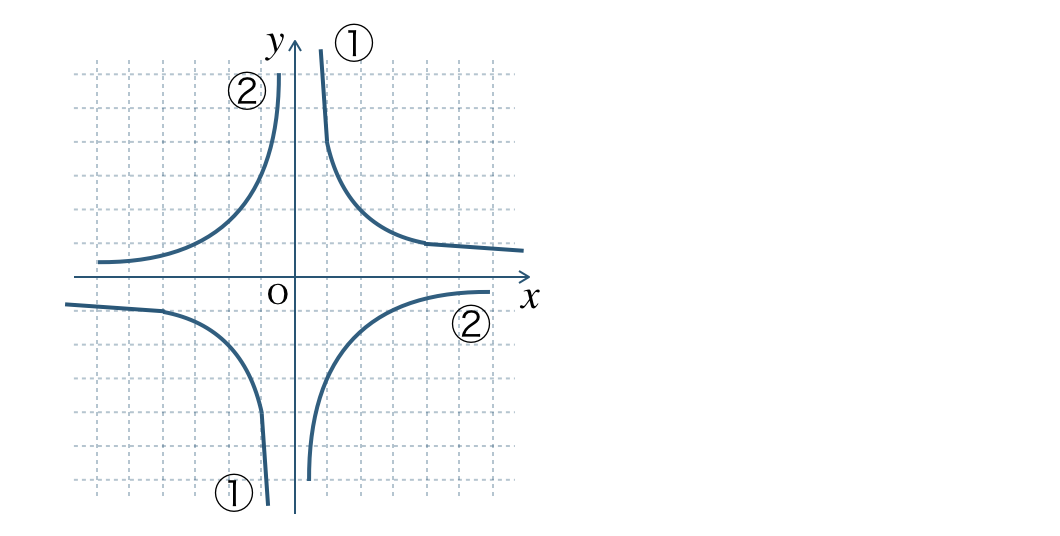
\({\small (2)}~\)次の①と②の双曲線のグラフを \(y\) を \(x\) の式で表せ。

解法のPoint
Point:グラフと比例の式
① グラフより、読み取りやすい点の座標をとる。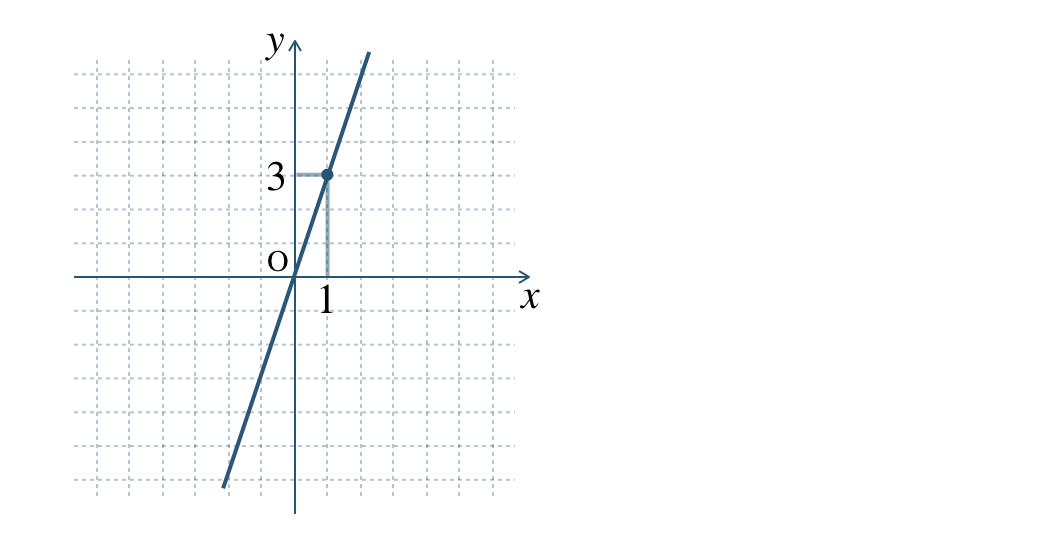
\(y=ax\) に \(x=1~,~y=3\) を代入すると、
\(\begin{eqnarray}~~~3&=&a\times 1\\[2pt]~~~a&=&3\end{eqnarray}\)
したがって、\(\begin{split}y=3x\end{split}\)
グラフから比例の式の求め方は、
① グラフより、読み取りやすい点の座標をとる。

② \(y=ax\) に点の座標を代入して、比例定数 \(a\) を求めて、比例の式を求める。
\(y=ax\) に \(x=1~,~y=3\) を代入すると、
\(\begin{eqnarray}~~~3&=&a\times 1\\[2pt]~~~a&=&3\end{eqnarray}\)
したがって、\(\begin{split}y=3x\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:グラフと反比例の式
① グラフより、読み取りやすい点の座標をとる。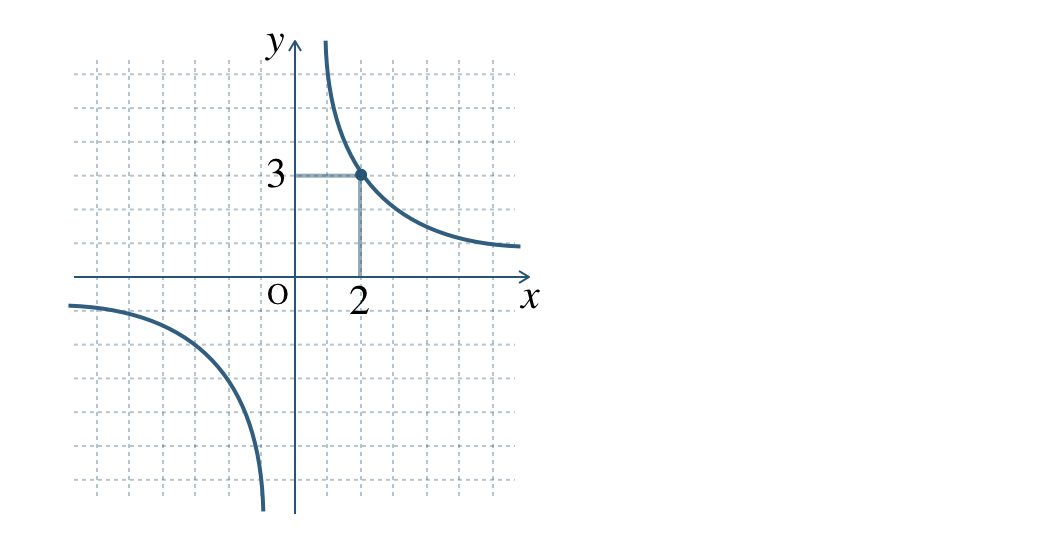
② \(\begin{split}y={\frac{\,a\,}{\,x\,}}\end{split}\) に点の座標を代入して、比例定数 \(a\) を求めて、反比例の式を求める。
\(\begin{split}y={\frac{\,a\,}{\,x\,}}\end{split}\) に \(x=2~,~y=3\) を代入すると、
\(\begin{eqnarray}~~~3&=&\frac{\,a\,}{\,2\,}\\[3pt]~~~a&=&6\end{eqnarray}\)
したがって、\(\begin{split}y=\frac{\,6\,}{\,x\,}\end{split}\)
グラフから反比例の式の求め方は、
① グラフより、読み取りやすい点の座標をとる。

② \(\begin{split}y={\frac{\,a\,}{\,x\,}}\end{split}\) に点の座標を代入して、比例定数 \(a\) を求めて、反比例の式を求める。
\(\begin{split}y={\frac{\,a\,}{\,x\,}}\end{split}\) に \(x=2~,~y=3\) を代入すると、
\(\begin{eqnarray}~~~3&=&\frac{\,a\,}{\,2\,}\\[3pt]~~~a&=&6\end{eqnarray}\)
したがって、\(\begin{split}y=\frac{\,6\,}{\,x\,}\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:グラフと比例・反比例の式
問題解説(1)
問題
\({\small (1)}~\)次の①と②の直線のグラフを \(y\) を \(x\) の式で表せ。
次の問いに答えよ。
\({\small (1)}~\)次の①と②の直線のグラフを \(y\) を \(x\) の式で表せ。

①
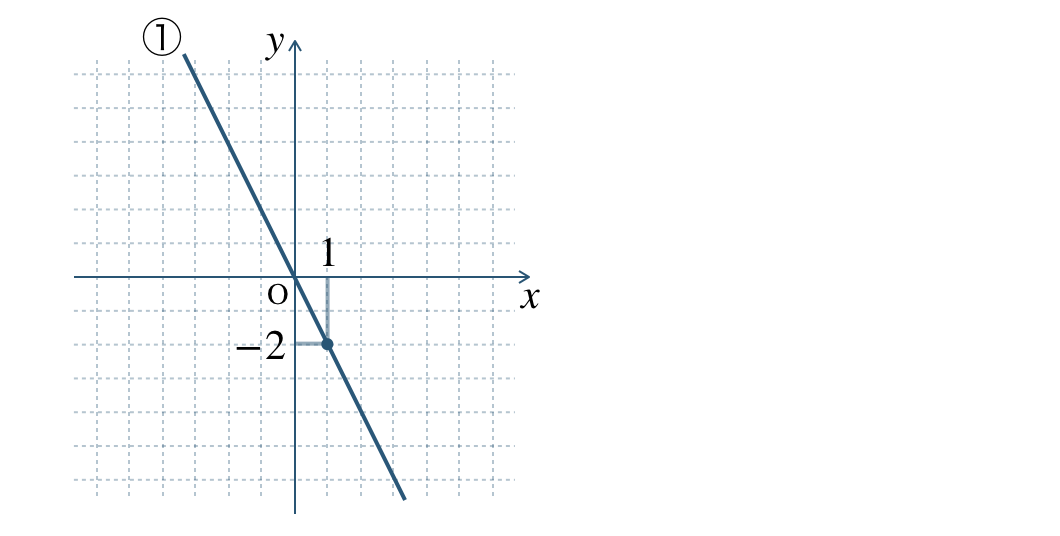
グラフが通る点 \((1~,~-2)\) より、
※ 他の点 \((-1~,~2)\) などでもよい。
\(y=ax\) に \(x=1~,~y=-2\) に代入すると、
\(\begin{eqnarray}~~~-2&=&a\times1\\[2pt]~~~-2&=&a\\[2pt]~~~a&=&-2\end{eqnarray}\)
したがって、\(\begin{split}y=-2x\end{split}\) となる
②
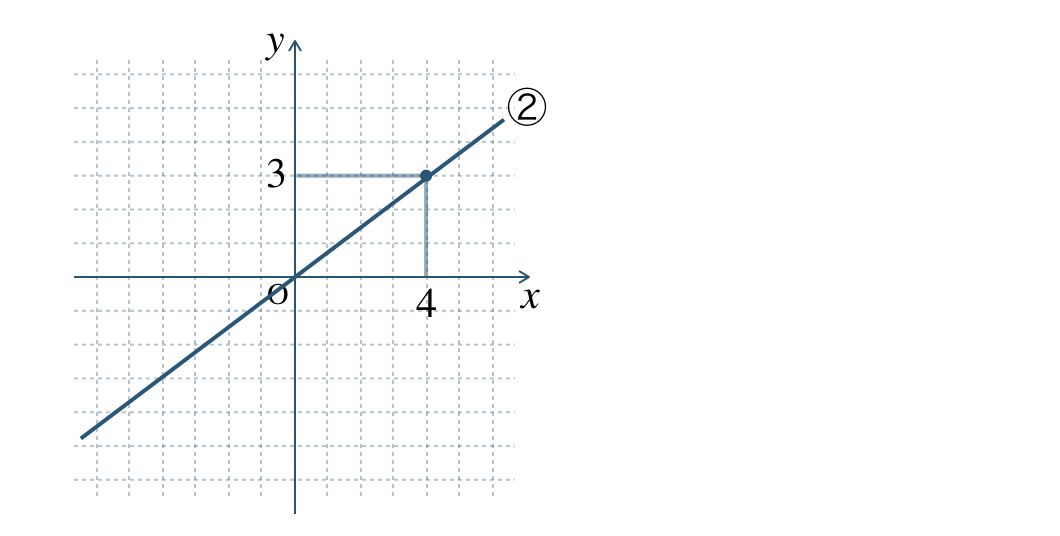
グラフが通る点 \((4~,~3)\) より、
※ 他の点 \((-4~,~-3)\) などでもよい。
\(y=ax\) に \(x=4~,~y=3\) に代入すると、
\(\begin{eqnarray}\hspace{20pt}~~~3&=&a\times4\\[2pt]~~~3&=&4a\end{eqnarray}\)
両辺を入れかえて、\(x\) の係数 \(4\) で両辺をわると、
\(\require{cancel} \begin{eqnarray}~~~4a&=&3\\[3pt]~~~\frac{\,4a\,}{\,4\,}&=&\frac{\,3\,}{\,4\,}\\[3pt]~~~\frac{\,\cancel{4}^{1}a\,}{\,\cancel{4}^{1}\,}&=&\frac{\,3\,}{\,4\,}\\[3pt]~~~a&=&\frac{\,3\,}{\,4\,}\end{eqnarray}\)
したがって、\(\begin{split}y=\frac{\,3\,}{\,4\,}x\end{split}\) となる
問題解説(2)
問題
\({\small (2)}~\)次の①と②の双曲線のグラフを \(y\) を \(x\) の式で表せ。
次の問いに答えよ。
\({\small (2)}~\)次の①と②の双曲線のグラフを \(y\) を \(x\) の式で表せ。

①
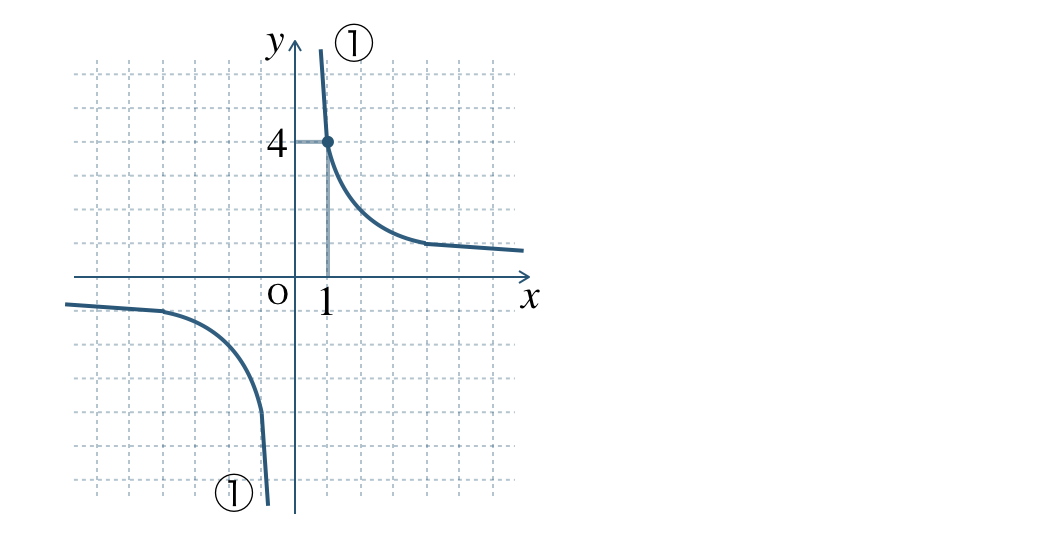
グラフが通る点 \((1~,~4)\) より、
※ 他の点 \((2~,~2)\) などでもよい。
\(\begin{split}y={\frac{\,a\,}{\,x\,}}\end{split}\) に \(x=1~,~y=4\) に代入すると、
\(\begin{eqnarray}~~~4&=&\frac{\,a\,}{\,1\,}\\[3pt]~~~4&=&a\\[2pt]~~~a&=&4\end{eqnarray}\)
したがって、\(\begin{split}y=\frac{\,4\,}{\,x\,}\end{split}\) となる
②
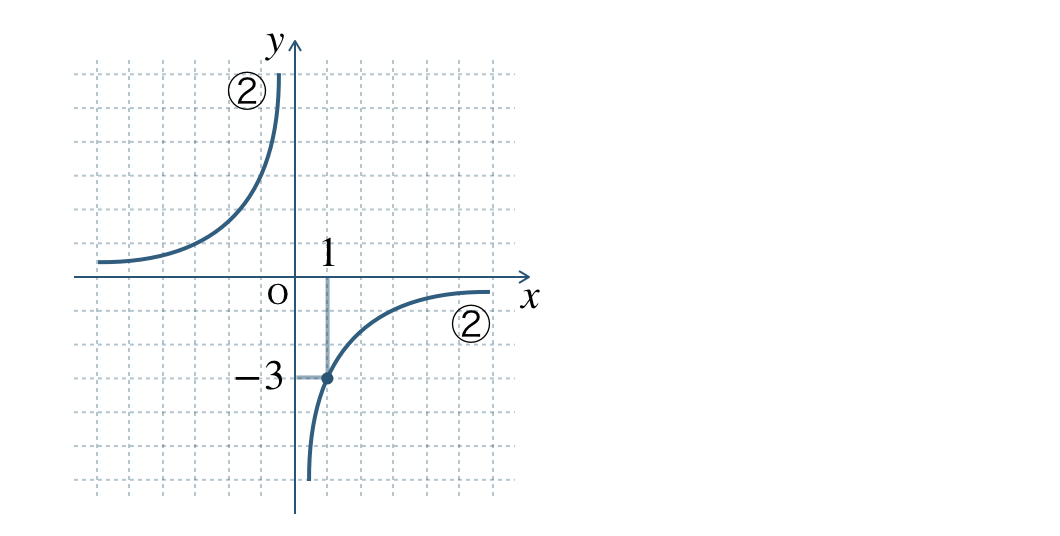
グラフが通る点 \((1~,~-3)\) より、
※ 他の点 \((-3~,~1)\) などでもよい。
\(\begin{split}y={\frac{\,a\,}{\,x\,}}\end{split}\) に \(x=1~,~y=-3\) に代入すると、
\(\begin{eqnarray}~~~-3&=&\frac{\,a\,}{\,1\,}\\[3pt]~~~-3&=&a\\[2pt]~~~a&=&-3\end{eqnarray}\)
したがって、\(\begin{split}y=-\frac{\,3\,}{\,x\,}\end{split}\) となる

【問題一覧】中1|比例と反比例
このページは「中学数学1 比例と反比例」の問題一覧ページとなります。解説の見たい単元名がわからないと...


