平面上の図形の表し方の解法
2点 \({\rm A~,~B}\) を通る直線を「直線 \({\rm AB}\) 」という。

直線 \({\rm AB}\) のうち、
\({\rm A}\) から \({\rm B}\) までの部分を「線分 \({\rm AB}\) 」という。

直線 \({\rm AB}\) のうち、
\({\rm A}\) から \({\rm B}\) の方向に限りなくのばした部分を「半直線 \({\rm AB}\) 」という。

■ 線分の長さ
線分 \({\rm AB}\) の長さを2点 \({\rm A~,~B}\) 間の距離といい、「 \({\rm AB}\) 」 で表す。
長さが等しいことを「 \({\rm AB=CD}\) 」と表す。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
■ 角の表し方
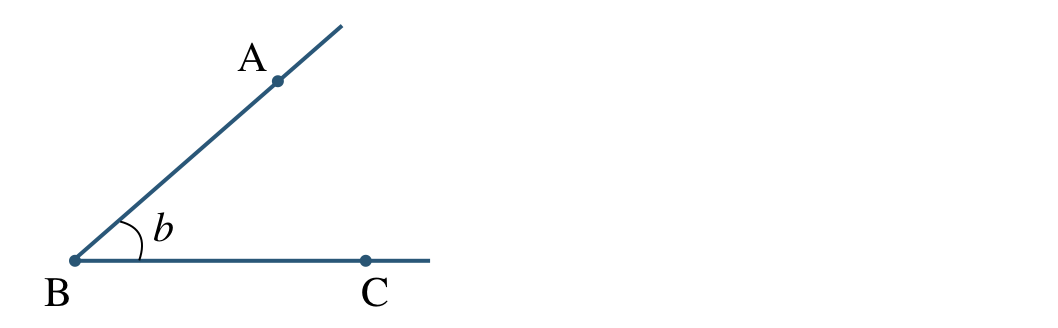
点 \({\rm B}\) から出る2つの半直線 \({\rm BA~,~BC}\) によってできる角を、
「 \(\angle{\rm ABC}\) 」で表し「角 \({\rm ABC}\) 」と読む。
また、「 \(\angle{\rm B}\) 」や「 \(\angle b\) 」と表すこともある。
■ 三角形の表し方
3つの頂点 \({\rm A~,~B~,~C}\) をもつ三角形 \({\rm ABC}\) を記号 \(\triangle\) を使い「 \(\triangle {\rm ABC}\) 」と表す。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
■ 2直線の垂直の表し方
2直線 \({\rm AB~,~CD}\) が垂直に交わるとき、
「 \({\rm AB\perp CD}\) 」と表し「 \({\rm AB}\) 垂直 \({\rm CD}\) 」と読む。このとき、一方の直線を他方の直線の「垂線」という。
また、点 \({\rm C}\) から直線 \({\rm AB}\) に垂線を引いたときの交点を \({\rm H}\) とすると、点 \({\rm C}\) と直線 \({\rm AB}\) との距離は線分 \({\rm CH}\) となる。
※ もっとも短いものが距離となる。

■ 2直線の平行の表し方
平面上の交わらない2直線 \({\rm AB~,~CD}\) は平行であり、「 \({\rm AB\,//\, CD}\) 」と表し、「 \({\rm AB}\) 平行 \({\rm CD}\) 」と読む。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:平面上の図形の表し方
問題解説(1)
\({\small (1)}~\)2点 \({\rm A~,~B}\) について、次のものを図で表せ。
① 直線 \({\rm AB}\) ② 線分 \({\rm AB}\)
③ 半直線 \({\rm AB}\) ④ 半直線 \({\rm BA}\)
① 2点 \({\rm A~,~B}\) をむすぶと、

② 直線 \({\rm AB}\) のうち、\({\rm A}\) から \({\rm B}\) までの部分より、

③ 点 \({\rm A}\) から \({\rm B}\) の方向に限りなくのばした部分より、

④ 点 \({\rm B}\) から \({\rm A}\) の方向に限りなくのばした部分より、

問題解説(2)
\({\small (2)}~\)次の問いに答えよ。
① 2点 \({\rm A~,~B}\) 間の距離を記号で表せ。
② 2つの線分 \({\rm AB~,~CD}\) の長さが等しいことを記号で表せ。
① 線分 \({\rm AB}\) の長さとなるので、
答えは \({\rm AB}\) となる
② 線分 \({\rm AB}\) の長さと線分 \({\rm CD}\) の長さが等しいので、
答えは \({\rm AB=CD}\) となる
問題解説(3)
\({\small (3)}~\)次の問いに答えよ。
① 図のような角を3つの表し方で表せ。

② 角 \({\rm A}\) と角 \({\rm B}\) の大きさが等しいことを記号で表せ。
③ 3点 \({\rm A~,~B~,~C}\) を頂点とする三角形を記号で表せ。
① 角 \({\rm ABC}\) を記号で表すと、\(\angle{\rm ABC}\)
点 \({\rm B}\) を使って表すと、\(\angle{\rm B}\)
\(b\) を使って表すと、\(\angle b\)
② \(\angle{\rm A}\) と \(\angle{\rm B}\) が等しくなるので、
答えは \(\angle{\rm A}=\angle{\rm B}\) となる
③ 三角形 \({\rm ABC}\) と記号で表すと、
答えは \(\triangle {\rm ABC}\) となる
問題解説(4)
\({\small (4)}~\)次の問いに答えよ。
① 2直線 \({\rm AB~,~CD}\) が垂直に交わることを記号で表せ。また、このとき一方の直線を他の直線の何というか答えよ。
② 次の図で、点 \({\rm C}\) と直線 \({\rm AB}\) との距離をア〜ウから選べ。

③ 2直線 \({\rm AB~,~CD}\) が平行であることを記号で表せ。
① 2直線 \({\rm AB~,~CD}\) が垂直に交わるので、
答えは \({\rm AB\perp CD}\) となる
また、一方の直線を他の直線の垂線という
② 点 \({\rm C}\) と直線 \({\rm AB}\) の距離は、点 \({\rm C}\) から直線 \({\rm AB}\) に垂線を引いた線分となるので、
答えは イ となる
③ 2直線 \({\rm AB~,~CD}\) が平行であるので、
答えは \({\rm AB\,//\, CD}\) となる



