問題:円とおうぎ形
\({\small (1)}~\)次の問いに答えよ。

① 円周の点 \({\rm A}\) から点 \({\rm B}\) までの部分を何というか答えよ。また、記号で表せ。
② 線分 \({\rm AB}\) を何というか答えよ。
③ \(\angle{\rm AOB}\) を何というか答えよ。
\({\small (2)}~\)次の問いに答えよ。
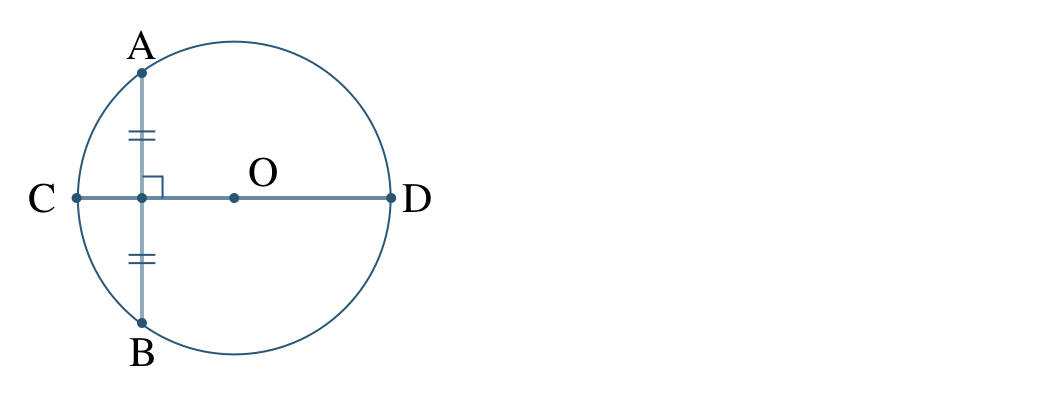
① 弦 \({\rm CD}\) が直径のとき、\(\overset{\frown}{\rm CD}\) に対する中心角を答えよ。
② 弦 \({\rm AB}\) と直径 \({\rm CD}\) の関係を答えよ。
\({\small (3)}~\)次の問いに答えよ。
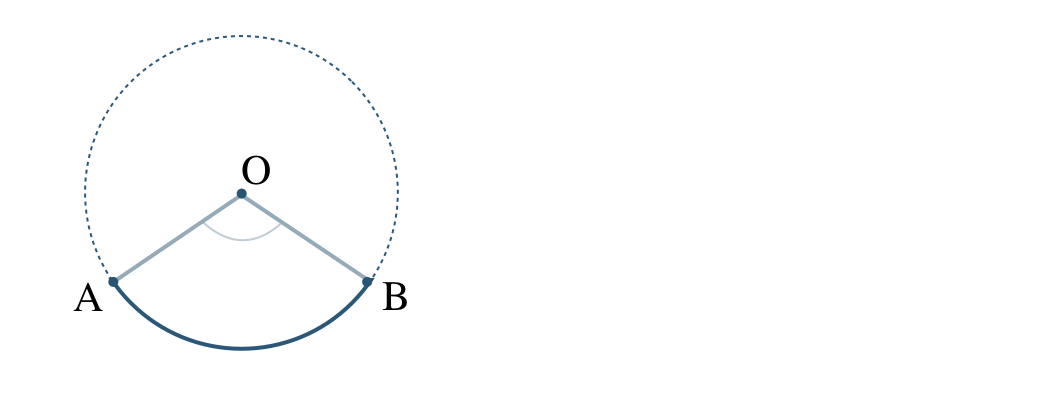
① 円と2つの半径とその弧で囲まれた図形を何というか答えよ。
② 2つの半径のつくる角を何というか答えよ。
解法のPoint

点 \({\rm O}\) を中心とする円を「円 \({\rm O}\) 」という。
中心 \({\rm O}\) から円周上の点を結ぶ線分はどの点をとっても等しい長さになり「円の半径」となる。
また、直径は「半径 \(\times 2\) 」となる。

円周上の2点 \({\rm A~,~B}\) をとると、円周の点 \({\rm A}\) から点 \({\rm B}\) までの部分を「弧 \({\rm AB}\) 」といい「 \(\overset{\frown}{\rm AB}\) 」と表す。
また、2つの半径 \({\rm OA~,~OB}\) によってできる \(\angle{\rm AOB}\) を「 \(\overset{\frown}{\rm AB}\) に対する中心角」といい、 \(\overset{\frown}{\rm AB}\) を「中心角 \(\angle{\rm AOB}\) に対する弧」という。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
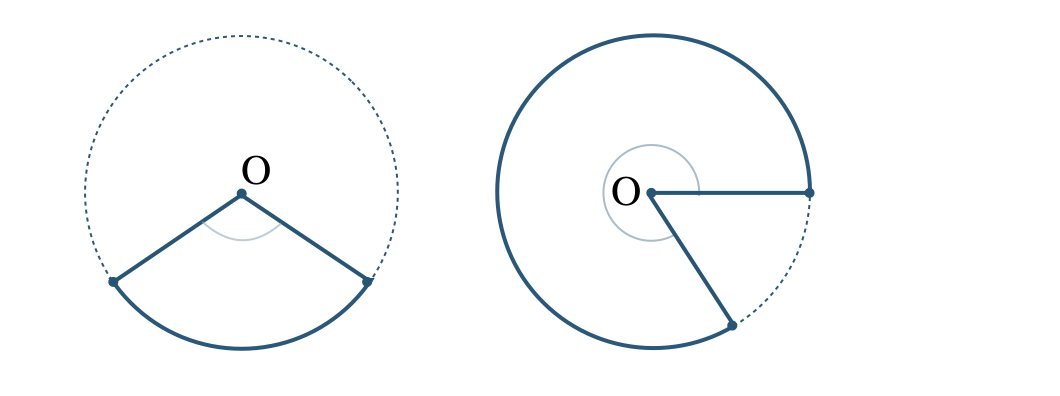
円の2つの半径とその弧で囲まれた図形を「おうぎ形」という。
また、2つの半径のつくる角を「そのおうぎ形の中心角」という。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:円とおうぎ形
問題解説(1)
\({\small (1)}~\)次の問いに答えよ。

① 円周の点 \({\rm A}\) から点 \({\rm B}\) までの部分を何というか答えよ。また、記号で表せ。
② 線分 \({\rm AB}\) を何というか答えよ。
③ \(\angle{\rm AOB}\) を何というか答えよ。
① 円周の一部を弧というので、
弧 \({\rm AB}\)、\(\overset{\frown}{\rm AB}\)
となる
② 円周上の2点を結ぶ線分を弦というので、
弦 \({\rm AB}\)
となる
③ 2つの半径 \({\rm OA~,~OB}\) によってできる角より、
\(\overset{\frown}{\rm AB}\) に対する中心角
となる
問題解説(2)
\({\small (2)}~\)次の問いに答えよ。

① 弦 \({\rm CD}\) が直径のとき、\(\overset{\frown}{\rm CD}\) に対する中心角を答えよ。
② 弦 \({\rm AB}\) と直径 \({\rm CD}\) の関係を答えよ。
① 直径 \({\rm CD}\) に対する中心角となるので、
\(180^\circ\)
となる
② 弦 \({\rm AB}\) の中点を通り、垂直に交わっているので、
直径 \({\rm CD}\) は弦 \({\rm AB}\) の垂直二等分線
となる
問題解説(3)
\({\small (3)}~\)次の問いに答えよ。

① 円と2つの半径とその弧で囲まれた図形を何というか答えよ。
② 2つの半径のつくる角を何というか答えよ。
① 半径 \({\rm OA~,~OB}\) と \(\overset{\frown}{\rm AB}\) で囲まれた図形であるので、
おうぎ形
となる
② 2つの半径 \({\rm OA~,~OB}\) のつくる角 \(\angle{\rm AOB}\) となるので、
おうぎ形の中心角
となる



